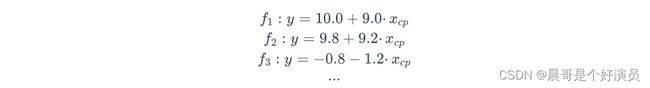回归模型介绍
Datawhale开源学习,机器学习课程,项目地址:https://github.com/datawhalechina/leeml-notes
首先讲机器学习中的:回归,回归Regression可以做哪些东西呢?
- 股票预测
输入为以往股票走势,预测未来走势
- 自动驾驶车辆
输入为无人驾驶检测的路况信息,输出为方向盘角度
- 推荐系统
输入为使用者A和商品B,输出为使用者A购买商品B的可能性
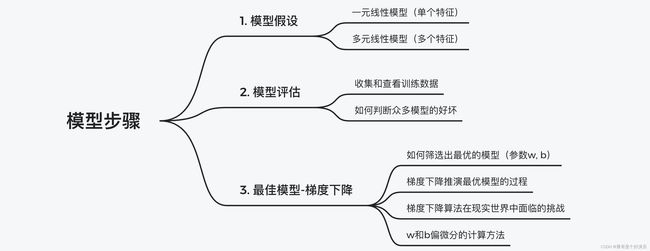
模型选择的步骤有三步:
- 模型假设(define a set of function),选择合适的模型,比如线性模型
- 模型评估(goodness of function),建立合适的损失函数,判断模型迭代时的收敛情况,可适当调整正则项
- 模型优化(pick the best function),通过梯度下降不断迭代,找到合适的解
那么以上这三步在之前的文章中也有提及,文章链接: 机器学习介绍
模型假设
首先是模型假设,比如对于线性模型而言,可以根据特征多少来划分其为多少元的线性模型,如果只有一个特征 x c p x_{cp} xcp,那么线性模型可假设为 y = b + ω ∗ x c p y=b+\omega*x_{cp} y=b+ω∗xcp,所以 ω \omega ω和 b b b可以猜测很多模型:
当然实际应用中,由于特征数量不止一个,可能最终的结果和多个特征强相关,那么每个特征都有其相应的权重,就拿pokman中生物的cp值来说,其可能收到多个特征的影响,比如:物种类型、物种血量、物种的重量、物种的高度等等,那这时候就不仅只有一个 x c p x_{cp} xcp作为特征,特征有 x c p 、 x h p 、 x w e i g h t x_{cp}、x_{hp}、x_{weight} xcp、xhp、xweight等等,用线性模型表示就是: y = b + ∑ ω i x i y=b+\sum \omega_i x_i y=b+∑ωixi。
- x i x_i xi表示了各种特征: x c p 、 x h p 、 x w e i g h t x_{cp}、x_{hp}、x_{weight} xcp、xhp、xweight等等
- w i w_i wi表示各类特征的权重: ω c p 、 ω h p 、 ω w e i g h t \omega_{cp}、\omega_{hp}、\omega_{weight} ωcp、ωhp、ωweight等等
- b b b为偏移量
以上就是模型假设,有「单特征模型」和「多特征模型」两种大致分类,后面两个步骤的说明,我以单特征为例进行说明,一是为了简洁,而是为了方便理解。
模型评估
对于单特征模型而言,要评估其模型的好坏,要将「预测模型」和「真实值」进行比对,求其方差即可。所以若有一系列预测数值,只需要统计真实值 y n y^n yn和预测值 f ( x c p n ) f(x^n_{cp}) f(xcpn)之间的方差即可,方差就是所谓的损失函数loss,即: ( y n − f ( x c p n ) ) 2 (y^n-f(x^n_{cp}))^2 (yn−f(xcpn))2。
比如统计10组原始数据的和,和越小模型越好,写出损失函数的公式就是:
L ( f ) = ∑ n = 1 10 ( y n − f ( x c p n ) ) 2 = ∑ n = 1 10 ( y n − ( b + ω ∗ x c p n ) ) 2 L(f)=\sum\limits_{n=1}^{10}(y^n-f(x^n_{cp}))^2=\sum\limits_{n=1}^{10}(y^n-(b+\omega*x^n_{cp}))^2 L(f)=n=1∑10(yn−f(xcpn))2=n=1∑10(yn−(b+ω∗xcpn))2
损失函数Loss分别由w和b确定,映射到二维坐标轴上时,就生成了一系列等高线,图像如下:
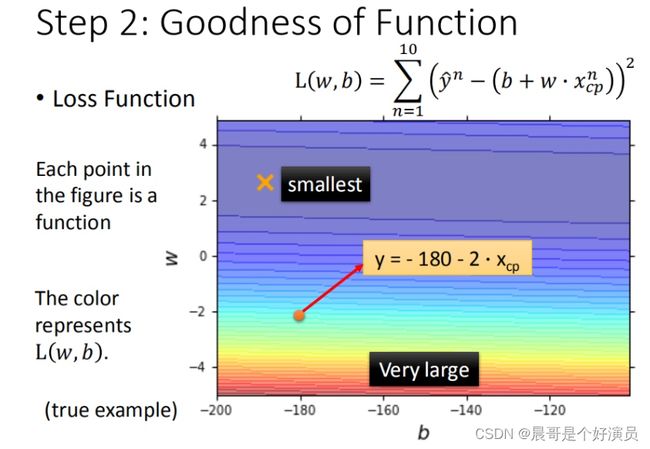
- 相同等高线的损失函数loss值是相同的
- 图中每个点代表模型对应的 ω \omega ω和 b b b
- 颜色越深loss越小,代表模型更优
最佳模型-梯度下降
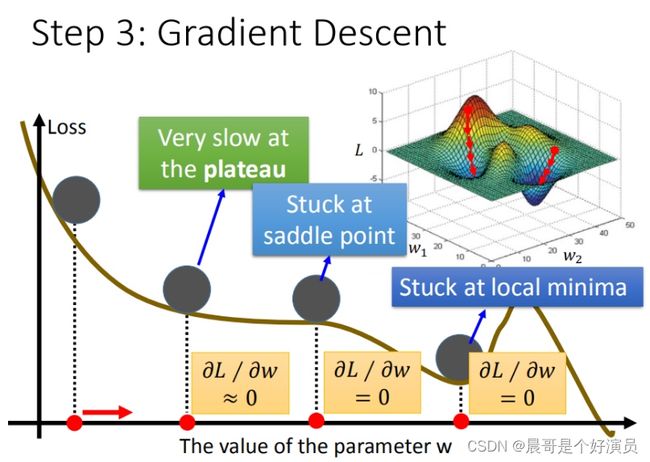
我们知道loss的大小决定了「预测模型」和「真实值」之间的差距,差距越小说明预测的越精准,因此就将问题转换成了求loss极小值的问题,也就是说,找到使得loss取最小值的w和b即可,那么我们可以通过梯度下降的方式不断迭代w和b的值,使得loss function迭代并取得一个极小值(这里之所以不一定取得最小值,是因为梯度下降不断迭代的时候可能只能陷入到某个极小值解中,而无法跳出该解,除非给梯度下降增加学习率,让其以更大幅度的迭代跳出当前的极小值而进入下一个极小值中,总之梯度下降便于我们去寻找极小值,而无法直接寻找到最小值),比如对于下图中的loss,计算对w的迭代:
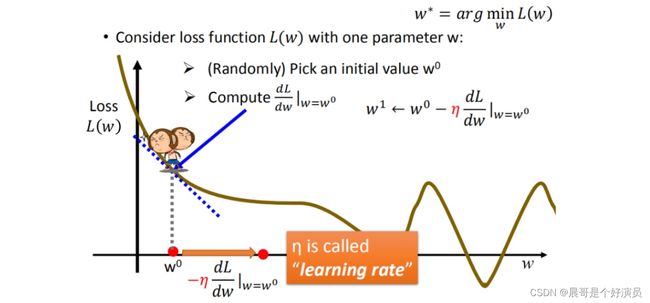
上面也说到了学习率,那么什么是学习率?学习率就是移动的步长,如上图的 η \eta η,接下来我们来说下梯度下降迭代步骤:
- 步骤1:随机选取一个权重 ω 0 \omega^0 ω0(之所以随机选取,是因为迭代过程中会让 ω 0 \omega^0 ω0自动修正到周围的极小值上去)
- 步骤2:计算微分,也就是当前的斜率,根据斜率来判断移动的方向
>0向右移动(增加 ω \omega ω)<0向左移动(减少 ω \omega ω)
- 步骤3:根据学习率移动
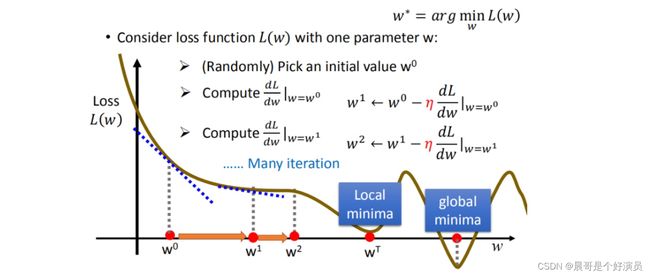
重复以上步骤2和步骤3,知道找到极小值,以上就是梯度下降的过程,只不过根据随机选取的 ω 0 \omega^0 ω0的不同,很可能不断迭代后得到不同的极小值,不一定是最终的最小值,如下图:
以上都只是在说单个模型参数 ω \omega ω,便于理解,接下来引入两个模型参数 ω \omega ω和 b b b,这个过程需要做偏微分,过程如下,分别对 ω \omega ω和 b b b求偏导:

在求偏导数并且不断迭代的过程中,最终的loss会渠道一个较小的结果,比如说对于下图而言,相同等高线代表相同的loss,越往中心,越接近极小值,那么这张图就是loss function在不断迭代时的一个行为轨迹,会按照等高线切线的发现方向前进,这就是「梯度下降」,即按照梯度的方向下降:
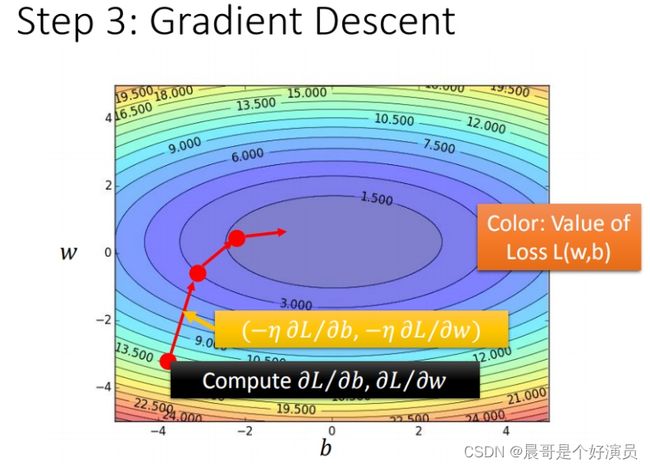
- 每一条线围成的圈就是等高线,代表损失函数的值,颜色约深的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向,也就是梯度下降的方向
那么以上就是梯度下降相关的知识,可以看到参数在迭代的过程中总是减去 η \eta η乘以对应参数关于loss的偏导数,根据其正负值进行迭代,那如果偏导数为0呢?或者趋近于0呢?又该如何解决?这也是梯度下降在当今现实世界中面临的挑战。
其实线性模型就是一个碗状模型,我们的目的就是找到最优解,但是往往由于很多模型的复杂性,导致在梯度下降的过程中,会出现偏导数为0或者趋近于0的情况,这样就会阻碍我们通过梯度下降去寻找最优解。
复杂模型与过拟合
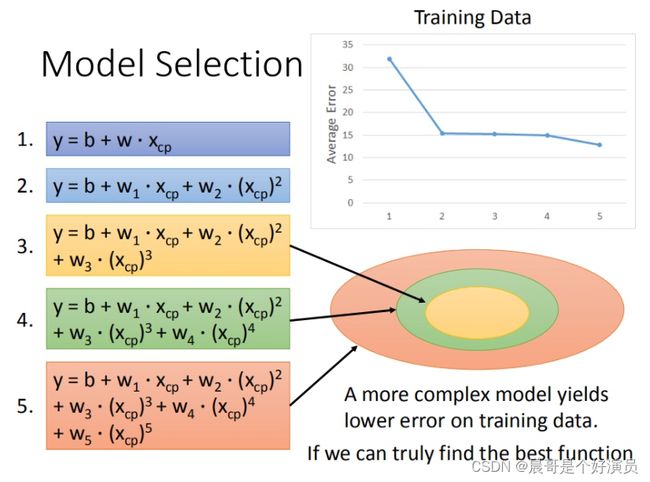
通常在选取模型的时候,我们根据现有的已知数据去选择适合当下数据的模型,我们知道,若要让模型能够更加准确的预测更多的数据,变的「普世性」更强一些,那么我们需要更多的数据去建立更复杂的模型才行,所以往往随着数据量的增加,线性模型的局限性就出现了,通常一开始我们的做法是,将一元一次的线性模型变为一元二次的线性模型,甚至三次、四次等等,使得我们的线性模型能够进行更加复杂的表示,来拟合更多的数据,随着模型不断变的复杂,也确实让测试的loss变的越来越小,拟合的数据也越来越准确,但是「越来越准确」的前提是「只是基于当前已有数据进行的拟合」,那这就会引出一个问题,叫做「过拟合」。
什么是过拟合?为了能够拟合当下数据,而不断增加模型复杂度,使得模型为了「拟合」而「拟合」,反而丧失了模型的「普世性」,当加入一个新的数据时,该数据可能并不能被已有模型很好的预测到。
由上图可以得出结论就是,越简单的模型是越复杂的模型的一个子集,也就是复杂模型能够拟合出更多的信息,但是往往「过多的信息」反而会影响到真实的预测。接下来就是:如果出现过拟合,我们该如何解决这样的问题呢?主要方法有以下三点:
- 将多个模型合并起来,然后根据类似于数字电路中的电平信号,来选取合适的项,其他项权重制为0
- 引入更多的特征,也就是之前提到的,将「单特征」模型变为「多特征」模型
- 加入正则化,正则化的引入使得模型的拟合可以变的「曲折」或者「平滑」,这取决于正则项中 λ \lambda λ值的大小