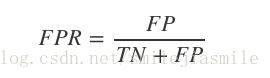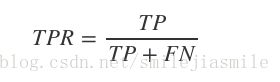模型评价(一) AUC大法 混淆矩阵
题记: 都说混淆矩阵易混淆,哈哈,下面就来试着尝试一下,看能不能帮助你更好的
理解混淆矩阵,以及 AUC 大法。
问题:
- AUC是什么
- AUC能拿来干什么
- AUC如何求解(深入理解AUC)
AUC是什么
混淆矩阵(Confusion matrix)
混淆矩阵是理解大多数评价指标的基础,毫无疑问也是理解AUC的基础。丰富的资料介绍着混淆矩阵的概念,这里用一个经典图来解释混淆矩阵是什么。
显然,混淆矩阵包含四部分的信息:
- True negative(TN),称为真阴率,表明实际是负样本预测成负样本的样本数
- False positive(FP),称为假阳率,表明实际是负样本预测成正样本的样本数
- False negative(FN),称为假阴率,表明实际是正样本预测成负样本的样本数
- True positive(TP),称为真阳率,表明实际是正样本预测成正样本的样本数
对照着混淆矩阵,很容易就能把关系、概念理清楚,但是久而久之,也很容易忘记概念。不妨我们按照位置前后分为两部分记忆,前面的部分是True/False表示真假,即代表着预测的正确性,后面的部分是positive/negative表示正负样本,即代表着预测的结果,所以,混淆矩阵即可表示为正确性-预测结果的集合。现在我们再来看上述四个部分的概念(均代表样本数,下述省略):
- TN,预测是负样本,预测对了
- FP,预测是正样本,预测错了
- FN,预测是负样本,预测错了
- TP,预测是正样本,预测对了
几乎我所知道的所有评价指标,都是建立在混淆矩阵基础上的,包括准确率、精准率、召回率、F1-score,当然也包括AUC。
ROC曲线
事实上,要一下子弄清楚什么是AUC并不是那么容易,首先我们要从ROC曲线说起。对于某个二分类分类器来说,输出结果标签(0还是1)往往取决于输出的概率以及预定的概率阈值,比如常见的阈值就是0.5,大于0.5的认为是正样本,小于0.5的认为是负样本。如果增大这个阈值,预测错误(针对正样本而言,即指预测是正样本但是预测错误,下同)的概率就会降低但是随之而来的就是预测正确的概率也降低;如果减小这个阈值,那么预测正确的概率会升高但是同时预测错误的概率也会升高。实际上,这种阈值的选取也一定程度上反映了分类器的分类能力。我们当然希望无论选取多大的阈值,分类都能尽可能地正确,也就是希望该分类器的分类能力越强越好,一定程度上可以理解成一种鲁棒能力吧。
为了形象地衡量这种分类能力,ROC曲线横空出世!如下图所示,即为一条ROC曲线(该曲线的原始数据第三部分会介绍)。现在关心的是:
- 横轴:False Positive Rate(假阳率,FPR)
- 纵轴:True Positive Rate(真阳率,TPR)
![]()
- 假阳率,简单通俗来理解就是预测为正样本但是预测错了的可能性,显然,我们不希望该指标太高。
- 真阳率,则是代表预测为正样本但是预测对了的可能性,当然,我们希望真阳率越高越好。
显然,ROC曲线的横纵坐标都在[0,1]之间,自然ROC曲线的面积不大于1。现在我们来分析几个特殊情况,从而更好地掌握ROC曲线的性质:
- (0,0):假阳率和真阳率都为0,即分类器全部预测成负样本
- (0,1):假阳率为0,真阳率为1,全部完美预测正确,happy
- (1,0):假阳率为1,真阳率为0,全部完美预测错误,悲剧
- (1,1):假阳率和真阳率都为1,即分类器全部预测成正样本
- TPR=FPR,斜对角线,预测为正样本的结果一半是对的,一半是错的,代表随机分类器的预测效果
于是,我们可以得到基本的结论:ROC曲线在斜对角线以下,则表示该分类器效果差于随机分类器,反之,效果好于随机分类器,当然,我们希望ROC曲线尽量除于斜对角线以上,也就是向左上角(0,1)凸。
AUC(Area under the ROC curve)
ROC曲线一定程度上可以反映分类器的分类效果,但是不够直观,我们希望有这么一个指标,如果这个指标越大越好,越小越差,于是,就有了AUC。AUC实际上就是ROC曲线下的面积。AUC直观地反映了ROC曲线表达的分类能力。
- AUC = 1,代表完美分类器
- 0.5 < AUC < 1,优于随机分类器
- 0 < AUC < 0.5,差于随机分类器
AUC能拿来干什么
从作者有限的经历来说,AUC最大的应用应该就是点击率预估(CTR)的离线评估。CTR的离线评估在公司的技术流程中占有很重要的地位,一般来说,ABTest和转全观察的资源成本比较大,所以,一个合适的离线评价可以节省很多时间、人力、资源成本。那么,为什么AUC可以用来评价CTR呢?我们首先要清楚两个事情:
- CTR是把分类器输出的概率当做是点击率的预估值,如业界常用的LR模型,利用sigmoid函数将特征输入与概率输出联系起来,这个输出的概率就是点击率的预估值。内容的召回往往是根据CTR的排序而决定的。
- AUC量化了ROC曲线表达的分类能力。这种分类能力是与概率、阈值紧密相关的,分类能力越好(AUC越大),那么输出概率越合理,排序的结果越合理。
我们不仅希望分类器给出是否点击的分类信息,更需要分类器给出准确的概率值,作为排序的依据。所以,这里的AUC就直观地反映了CTR的准确性(也就是CTR的排序能力)
AUC如何求解
步骤如下:
- 得到结果数据,数据结构为:(输出概率,标签真值)
- 对结果数据按输出概率进行分组,得到(输出概率,该输出概率下真实正样本数,该输出概率下真实负样本数)。这样做的好处是方便后面的分组统计、阈值划分统计等
- 对结果数据按输出概率进行从大到小排序
- 从大到小,把每一个输出概率作为分类阈值,统计该分类阈值下的TPR和FPR
- 微元法计算ROC曲线面积、绘制ROC曲线
代码如下所示:
import pylab as pl
from math import log,exp,sqrt
import itertools
import operator
def read_file(file_path, accuracy=2):
db = [] #(score,nonclk,clk)
pos, neg = 0, 0 #正负样本数量
#读取数据
with open(file_path,'r') as fs:
for line in fs:
temp = eval(line)
#精度可控
#score = '%.1f' % float(temp[0])
score = float(temp[0])
trueLabel = int(temp[1])
sample = [score, 0, 1] if trueLabel == 1 else [score, 1, 0]
score,nonclk,clk = sample
pos += clk #正样本
neg += nonclk #负样本
db.append(sample)
return db, pos, neg
def get_roc(db, pos, neg):
#按照输出概率,从大到小排序
db = sorted(db, key=lambda x:x[0], reverse=True)
file=open('data.txt','w')
file.write(str(db))
file.close()
#计算ROC坐标点
xy_arr = []
tp, fp = 0., 0.
for i in range(len(db)):
tp += db[i][2]
fp += db[i][1]
xy_arr.append([fp/neg,tp/pos])
return xy_arr
def get_AUC(xy_arr):
#计算曲线下面积
auc = 0.
prev_x = 0
for x,y in xy_arr:
if x != prev_x:
auc += (x - prev_x) * y
prev_x = x
return auc
def draw_ROC(xy_arr):
x = [_v[0] for _v in xy_arr]
y = [_v[1] for _v in xy_arr]
pl.title("ROC curve of %s (AUC = %.4f)" % ('clk',auc))
pl.xlabel("False Positive Rate")
pl.ylabel("True Positive Rate")
pl.plot(x, y)# use pylab to plot x and y
pl.show()# show the plot on the screen数据:提供的数据为每一个样本的(预测概率,真实标签)tuple
数据链接:https://pan.baidu.com/s/1c1FUzVM,密码1ax8
计算结果:AUC=0.747925810016,与Spark MLLib中的roc_AUC计算值基本吻合
当然,选择的概率精度越低,AUC计算的偏差就越大
总结
- ROC曲线反映了分类器的分类能力,结合考虑了分类器输出概率的准确性
- AUC量化了ROC曲线的分类能力,越大分类效果越好,输出概率越合理
- AUC常用作CTR的离线评价,AUC越大,CTR的排序能力越强
注: 转载自 https://segmentfault.com/a/1190000010410634