视觉SLAM十四讲学习笔记----ch3 Eigen代码实践
目录
- 1. 编译
- 2. Eigen代码实践
-
- 2 .1运行use Eigen
- 2.2. Eigen几何模块
- 2.3.当前焦点坐标位置
- 2.4. 可视化显示
- 2.5. 显示相机的位姿
- 2.6 补充Pangolin库使用知识
- 2.7章节总结
1. 编译
cmake:根据CMakeList.txt的内容生成编译文件CMakeFiles
make:根据CMakeFiles以及源文件生成可执行文件
mkdir build
cd build
cmake ..
make
2. Eigen代码实践
2 .1运行use Eigen
#include ,即三维向量
Vector3d v_3d;
// 这是一样的
Matrix<float, 3, 1> vd_3d;
// Matrix3d 实质上是 Eigen::Matrix result_wrong_type = matrix_23 * v_3d;
// 应该显式转换
Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;//强制类型转换,matrix_23.cast result_wrong_dimension = matrix_23.cast() * v_3d;
// 一些矩阵运算
// 四则运算就不演示了,直接用+-*/即可。
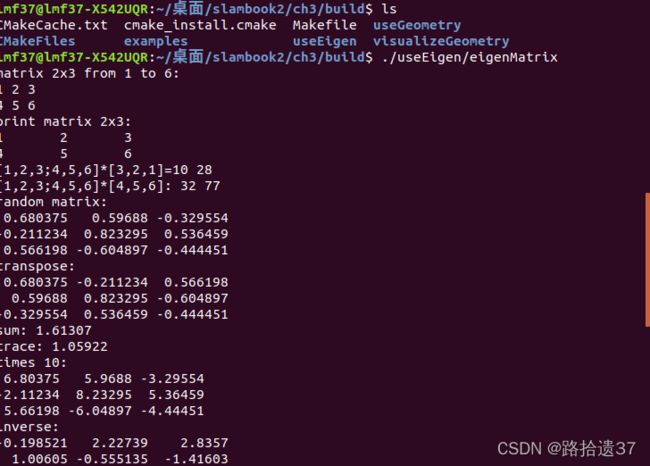
matrix_33 = Matrix3d::Random(); // 随机数矩阵
cout << "random matrix: \n" << matrix_33 << endl;
cout << "transpose: \n" << matrix_33.transpose() << endl; // 转置
cout << "sum: " << matrix_33.sum() << endl; // 各元素和
cout << "trace: " << matrix_33.trace() << endl; // 迹
cout << "times 10: \n" << 10 * matrix_33 << endl; // 数乘
cout << "inverse: \n" << matrix_33.inverse() << endl; // 逆
cout << "det: " << matrix_33.determinant() << endl; // 行列式
// 特征值
// 实对称矩阵可以保证对角化成功
//作用于一个有限维的内积空间,一个自伴算子(self-adjoint operator)等于自己的伴随算子;等价地说,在一组单位酉正交基下,表达自伴算子的矩阵是埃尔米特矩阵。
//埃尔米特矩阵等于自己的共轭转置。根据有限维的谱定理,必定存在着一个正交归一基,可以表达自伴算子为一个实值的对角矩阵。
SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;//特征值
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;//特征向量
// 解方程
// 我们求解 matrix_NN * x = v_Nd 这个方程
// N的大小在前边的宏里定义,它由随机数生成
// 直接求逆自然是最直接的,但是求逆运算量大
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN
= MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证半正定
Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);
clock_t time_stt = clock(); // 计时
// 直接求逆
Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
cout << "time of normal inverse is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
// 通常用矩阵分解来求,例如QR分解,速度会快很多
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout << "time of Qr decomposition is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
// 对于正定矩阵,还可以用cholesky分解来解方程
time_stt = clock();
x = matrix_NN.ldlt().solve(v_Nd);
cout << "time of ldlt decomposition is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
return 0;
}
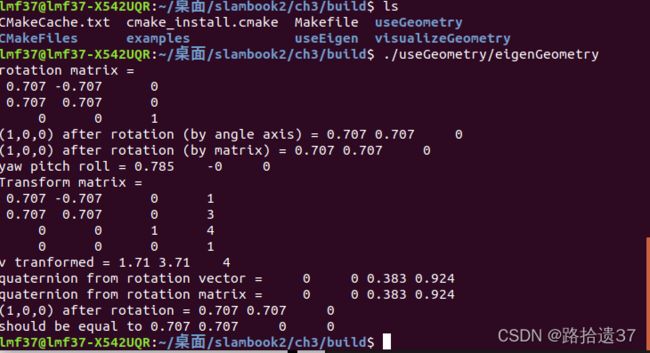
2.2. Eigen几何模块
#include 2.3.当前焦点坐标位置
补充知识!!!
视觉SLAM十四讲实践之坐标系之间的欧式变换
 代码及注释如下:
代码及注释如下:
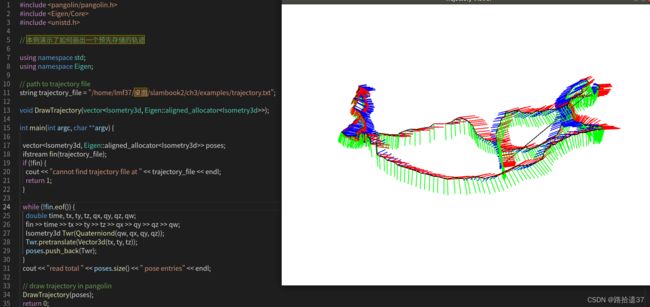
#include 2.4. 可视化显示
// path to trajectory file
string trajectory_file = "/home/lmf37/桌面/slambook2/ch3/examples/trajectory.txt";
//这里需要修改一下路径,因为新建了build文件,可以用绝对路径替代,这样出错率降低
代码及注释如下:
#include 在尝试读懂代码的同时,又顺便补充了一下OpenGL中glVertex*函数知识
glVertex2d
glVertex2f
glVertex3d
glVertex3f
glVertex3fv
and so on
/*
数字代表维度,也是参数列表的个数
字母表示参数的类型
s 表示 16位整数(OpenGL 中将这个类型定义为GLshort),
i 表示32位整数(OpenGL 中将这个类型定义为 GLint 和GLsizei ),
f 表示32 位浮点数(OpenGL 中将这个类型定义为GLfloat 和GLclampf),
d 表示 64 位浮点数(OpenGL 中将这个类型定义为GLdouble 和GLclampd )。
v 表示传递的几个参数将使用指针的方式。
*/
//这些函数除了参数的类型和个数不同以外,功能是相同的。例如,以下五个代码段的功能是等效的:
glVertex2i ( 1, 3 );
glVertex2f ( 1.0f, 3.0f );
glVertex3f ( 1.0f, 3.0f, 0.0f );
glVertex4f ( 1.0f, 3.0f, 0.0f, 1.0f );
GLfloat VertexArr3[] = {1.0f, 3.0f, 0.0f}; glVertex3fv ( VertexArr3 );
2.5. 显示相机的位姿

代码及注释如下:(这部分代码,还未完全啃透,留一个坑待填!!!)
#include 2.6 补充Pangolin库使用知识
Pangolin是对OpenGL进行封装的轻量级的OpenGL输入/输出和视频显示的库。可以用于3D视觉和3D导航的视觉图,可以输入各种类型的视频、并且可以保留视频和输入数据用于debug。
使用教程参考:
3D绘图程序库Pangolin安装以及快速入门,使用教程介绍详细
学习参考资料:
【1】Pangolin:
【2】Pangolin安装问题:
【3】examples
【4】Pangolin的使用:
【5】特性:
2.7章节总结
这一章内容讲的就是如何描述物体的刚体运动,也不严谨的描述为:如何描述相机在三维空间中的运动
首先提出了:运动由旋转+平移组成
拆开来看:
首先描述旋转:就提出了 旋转矩阵、旋转向量、欧拉角、四元数。这些方法都可以用来描述旋转
(所以,这四个表示方法之间也是可以相互转化的,尤其是编程下的相互转化,要掌握)
平移比较好描述,一个平移向量
那么,我们如何描述运动?
对一个坐标,先将其旋转(四种方法),再加上平移向量,就得到了其运动后的坐标。
但是,由于这里面要加上平移向量,所以就有一个问题,这个运动变化描述出来不是线性的
所以我们用一些数学技巧(齐次坐标),使得可以用一个矩阵来将旋转+平移包含在一起,这就是变换矩阵。
到此,本讲内容就结束了,我们用一个变换矩阵简洁的解决了描述物体运动的问题。
此部分需要的数学及理论知识转此学习