ECCV2020 Detection DETR 论文解读

End-to-End Object Detection with Transformers

论文链接：https://www.ecva.net/papers/eccv_2020/papers_ECCV/papers/123460205.pdf

论文代码：https://github.com/facebookresearch/detr

Abstract: We present a new method that views object detection as a direct set prediction problem. Our approach streamlines the detection pipeline, effectively removing the need for many hand-designed components like a non-maximum suppression procedure or anchor generation that explicitly encode our prior knowledge about the task. The main ingredients of the new framework, called DEtection TRansformer or DETR, are a set-based global loss that forces unique predictions via bipartite matching, and a transformer encoder-decoder architecture. Given a fixed small set of learned object queries, DETR reasons about the relations of the objects and the global image context to directly output the final set of predictions in parallel. The new model is conceptually simple and does not require a specialized library, unlike many other modern detectors. DETR demonstrates accuracy and run-time performance on par with the well-established and highly-optimized Faster RCNN baseline on the challenging COCO object detection dataset. Moreover, DETR can be easily generalized to produce panoptic segmentation in a unified manner. We show that it significantly outperforms competitive baselines. Training code and pretrained models are available at https://github.com/facebookresearch/detr.

图1 DETR将通用CNN与Transformer架构相结合，直接（并行）预测最终检测集。在训练过程中，二部匹配使用GT唯一地分配预测。不匹配的预测无对象类别

检测中的direct set 预测有两个要素至关重要：1)一组预测损失，强制在prediction和GT之间进行唯一匹配；2)预测（在一次过程中）一组对象并对其关系建模的体系结构。我们在图2中详细描述了我们的体系结构。

1 目标检测的预测损失

DETR在一次过程的decoder阶段，采用一组固定大小的N个预测结果，N设置为明显大于图像中对象的数量。（即当$N=100$，那么DETR最多只能预测图片中100个目标）。训练的主要困难之一是根据地面真实情况对预测对象（类别[class]、位置[position x y]、大小[size w h]）进行评分。我们的损失在predictions和GT之间产生最佳的二部匹配，然后优化特定对象（边界框）的损失。

我们用$y$表示GT的目标，用$\hat{y}=\{{\hat{y}}_i{\}}_{i=1}^N$表示N个predictions结果。需要注意的是设置N的时候，它需要比图像中出现的目标数更大，我们把$y$设置成一组大小为N的GT，不足的用无目标(no object)填充。为了找到$y$集合和$\hat{y}$集合的二部图匹配，我们寻找成本最低的N个元素$\sigma \in {\mathfrak{S}}_N$的组合：
$$\hat{\sigma }=\underset{\sigma \in {\mathfrak{S}}_N}{\mathrm{argmin}}\sum _i^N{\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$$
其中${\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$是$y_i$和$\sigma (i)$的匹配代价。本文依据前人工作，使用匈牙利算法有效地计算了此最优分配。匹配代价考虑了class prediction以及predictions和GT的相似性。每个GT的元素$i$都能看作是$y_i=(c_i,b_i)$，其中$c_i$表示目标的类别标签（包含不是目标的标签），$b_i=[0,1{]}^4$表示定义GT的box在图片中的位置向量，一般是$[x,y,w,h]$的变种和归一化。对于索引$\sigma (i)$的预测，我们定义了类的概率$c_i$为${\hat{p}}_{\sigma (i)}(c_i)$以及预测框的位置${\hat{b}}_{\sigma (i)}$。就是对于每个预测结果，根据其预测的N个结果，对N个GT做匹配，得到$N\times N$的矩阵，用匈牙利算法去解，而构建代价矩阵的信息就是自己的预测类别概率和目标框定位精准程度。

这种寻找匹配的过程与现有检测器中用于将建议或锚与地面真实对象匹配的启发式分配规则起着相同的作用。主要区别在于，我们需要找到一个一对一的匹配机制来进行无重复的直接集预测。

第二步是计算损失函数，即前一步中匹配的所有对的匈牙利损失。我们对损失的定义类似于常见目标检测器的损失，即类预测的负对数似然和后面定义的检测框损失的线性组合
$${\mathcal{L}}_{\text{Hungarian }}(y,\hat{y})=\sum _{i=1}^N\left[-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\text{box }}\left(b_i,{\hat{b}}_{\hat{\sigma }}(i)\right)\right]$$

这里分为两部分：

1. 通过匈牙利算法匹配100个GT（有目标的和没有目标的）与预测结果做二部图匹配，得到一对一结果——类似于anchor和GT的匹配策略
   $$\hat{\sigma }=\underset{\sigma \in {\mathfrak{S}}_N}{\mathrm{argmin}}\sum _i^N{\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$$

2. 通过计算Hungarian loss，做反向传播——类似于目标检测算法的loss构建
   $${\mathcal{L}}_{\text{Hungarian }}(y,\hat{y})=\sum _{i=1}^N\left[-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\text{box }}\left(b_i,{\hat{b}}_{\hat{\sigma }}(i)\right)\right]$$
   $L_{box}$是GIOU loss和L1 loss的集合
   $${\mathcal{L}}_{box}(b_i,{\hat{b}}_{\sigma (i)})={\lambda }_{\text{iou }}{\mathcal{L}}_{\text{iou }}\left(b_i,{\hat{b}}_{\sigma (i)}\right)+{\lambda }_{\mathrm{L}1}{\Vert b_i-{\hat{b}}_{\sigma (i)}\Vert }_1$$

其中$\hat{\sigma }$是第一步计算的最优分配。在实践中，当$c_i=\varnothing$时，我们将对数概率项的权重降低了10倍保证正负样本平衡。且目标和非目标之间的匹配代价不依赖于检测结果，即图中目标数确定，其代价就是固定的。

2 DETR结构

图2 DETR使用CNN作为backbone去学习输入图像的特征。该模型将其展平，并在将其传递到transformer编码器之前使用位置编码对其进行补充。然后，transformer解码器将少量固定数量的已学习位置嵌入作为输入，我们称之为对象查询，并额外处理编码器输出。我们将解码器的每个输出嵌入传递给共享前馈网络（FFN），该网络预测检测（类和边界框）或（无对象类）。

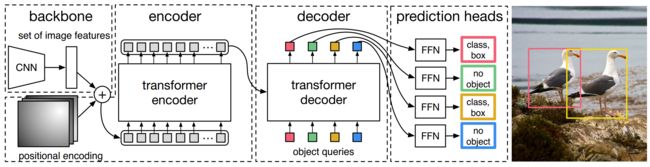
DETR结构如图2所示，它包含三个组件，CNN backbone用来提取图像特征，encoder-decoder网络，feed forward network得到最终预测。

与许多现有检测器不同，DETR可以在任何深度学习框架中实现，该框架提供了一个通用的CNN主干网络和一个只有几百行代码的Transformer架构实现。在PyTorch中，DETR的推理代码可以在不到50行中实现。

2.1 Backbone

初始化的RGB图像中$x_{\mathrm{i}\mathrm{m}\mathrm{g}}\in {\mathbb{R}}^{3\times H_0\times W_0}$，CNN获得低分辨率特征图$f\in {\mathbb{R}}^{C\times H\times W}$。其值我们设置为$C=2048$，$H,W=\frac{H_0}{32},\frac{W_0}{32}$

2.2 Transformer encoder

首先，$1\times 1$卷积将高阶特征$f$的通道维数从C降低到更小的维数d。创建新的特征图$z_0\in {\mathbb{R}}^{d\times H\times W}$。编码器需要一个序列作为输入，因此我们将$z_0$的空间维度压缩为一维，从而生成$d\times HW$特征图。每个编码器层都有一个标准体系结构，由一个多头自注意力模块和一个前馈网络（FFN）组成。由于transformer体系结构是置换不变的，因此我们使用固定位置编码对其进行补充，这些编码被添加到每个注意层的输入中。

2.3 Transformer decoder

解码器遵循转换器的transformer架构，使用多头自注意力和编码器-解码器注意机制转换大小为d的N个嵌入。与原始transformer的不同之处在于，我们的模型在每个解码器层并行解码N个对象，而A使用自回归模型，该模型一次预测一个元素的输出序列。由于解码器也是置换不变的，因此N个输入嵌入必须不同才能产生不同的结果。这些输入嵌入是学习的位置编码，我们称之为对象查询，与编码器类似，我们将它们添加到每个注意层的输入中。解码器将N个对象查询转化为一个输出嵌入。然后，通过前馈网络（在下一小节中描述）将它们独立解码为方框坐标和类标签，从而得到N个最终预测。该模型利用自身和编码器-解码器对这些嵌入的关注，利用对象之间的成对关系对所有对象进行全局推理，同时能够将整个图像用作上下文。

2.4 feed forward networks(FFN)

最终的预测由一个具有ReLU激活函数和隐藏层数为d的三层感知器和一个线性投影层推理。FFN预测输入图像中box的归一化中心坐标、高度和宽度，线性层使用softmax函数预测类别标签。由于我们预测了一个由N个边界框组成的固定大小集，其中N通常比图像中感兴趣对象的实际数量大得多，因此使用了一个额外的特殊类标签$\varnothing$来表示在插槽中未检测到任何对象。该类与标准对象检测方法中的background类起着类似的作用。

2.5 Auxiliary decoding losses

我们发现，在训练过程中，在解码器中使用auxiliary losses很有帮助，尤其是有助于模型输出每个类的正确对象数。每个解码器层的输出都用了共享的layer-norm，然后到共享预测头（分类和框预测）。然后，我们像往常一样将匈牙利损失用于监督。