详解 空域图像增强+频域图像增强

空域图像增强+频域图像增强

---

前言

图像处理基础知识也很重要，不然在matlab里键入代码就是一头雾水，今天是空域图像增强和频域图像增强</font>

---

空域图像增强

空域：指图像平面本身
【频域：对图像进行傅里叶变换等频域变换】
空域图像增强：
直接作用于像素改变其特性的增强方法

• 点操作
• 模板操作/领域操作：板操作则主要通过设计模板系数来实现不同的增强操作

图像的数据结构：uint8 ，uint16 , double

一.灰度映射：点处理

灰度级范围不变

1.图像求反（将灰度值翻转）

反转变换表达式：

						t = (L-1)-s 
		(L为总的灰度级数，s为当前灰度级）

matlab实例如下：

A = imread('circuit.tif');
B = 255 - A;
subplot(121);imshow(A);title('原图');
subplot(122);imshow(B);title('图像求反');

2.对数变换（动态范围压缩）

动态范围压缩：与增强对比度相反

		t = C log( 1 + |s| )

A = imread('circuit.tif');
c = 50
B = c*log(double(A)+1);
subplot(121);imshow(A);title('原图');
subplot(122);imshow(uint8(B));title('对数变换');

用途：扩展暗区

3.幂次变换

			s = c*r^γ

具有对数变换相似的作用，但是更加灵活
γ>1压缩灰度
γ<1扩展灰度

f1 = imread('lena.bmp');
f = rgb2gray(f1);
minvalue = double(min(min(f)));
maxvalue = double(max(max(f)));
range = maxvalue - minvalue;
Min = 0;
Max = 255;
Range = Max - Min;
f = Range * (double(f) - minvalue)/range + Min;
%对图像进行灰度归一化实现f = mat2gray(I,[0,255]);功能
Gamma = 0.9;%设定gamma的值
s1 =double(f).^Gamma;%进行gamma变换
Gamma = 1.2;
s2 =double(f).^Gamma;
figure;
subplot(1,3,1);
imshow(uint8(f));
title('原图');
subplot(1,3,2);
imshow(uint8(s1));
title('伽玛变换（gamma=0.9）');
subplot(1,3,3);
imshow(uint8(s2));
title('伽玛变换（gamma=1.2）');

结果：
γ>1压缩灰度，细节丢失
γ<1扩展灰度

4.阶梯量化

将图像灰度分阶段量化成较少的级数，达到数据量压缩的效果
（将图像灰度分阶段量化成较少的级数，这可在保持原图动态范围的基础上，减少灰度级数，即减少表示灰度所需的比特数，从而获得数据量压缩的效果。这里的映射是多对一的，不仅灰度值s会映射成灰度值t，而且在灰度值s前后一定范围内的灰度值也会映射成灰度值t ）

5.阈值切分（二值化）

大于阈值255
小于阈值 0
对比度最大但是细节全丢失了

f = imread('circuit.tif');
thresh = graythresh(f);     %自动确定二值化阈值
f1 = im2bw(f,thresh);
subplot(121);
imshow(f);
title('原图');
subplot(122);
imshow(f1);
title('二值化');

（有点艺术那味了，喜欢hhh)

6.分段线性变换函数

二.图像运算：集合处理

1.算术运算（对灰度图像）:

加减乘除
上面各运算的含义是指通过算术运算从两个像素的灰度值得到一个新的灰度值，作为对应结果新图像相同位置处像素的灰度值。新灰度值有可能超出原图像的动态范围，此时常需要进行灰度映射，以将运算结果的灰度值限制在或调整到原图像允许的动态范围内

加法：

用图像平均消除随机噪声
（噪声互不相关，且具有零均值）
高斯噪声？

减法：

设有图像f(x, y)和h(x, y)，对它们进行相减运算，显示两幅图像间的差异
——可用于运动检测（照明恒定，差值不为0处表示像素有移动）

2.逻辑运算（二值图，逻辑图）：与/或/非

三.直方图修正：直方图处理

1.图像的直方图：反映了图像的基本灰度级特征（暗，亮，低对比度，高对比度）
借助对图像直方图的修改或变换，可以改变图像像素的灰度分布，从而达到对图像进行增强的目的

直方图均衡化

Aim: 增强动态范围偏小的图像的反差
个方法的基本思想是把原始图的直方图变换为在整个灰度范围内均匀分布的形式，这样就增加了像素灰度值的动态范围，从而可达到增强图像整体对比度的效果
对累计直方图重新量化，形成基本均匀的分布

f = imread('baboon1.bmp');
f = rgb2gray(f);%灰度化
[m,n] = size(f);
GP = zeros(1,256);
for k = 0:255
    GP(k+1) = length(find(f == k))/(m*n);
end
S1=zeros(1,256);
for i = 1:256
    for j = 1:i
        S1(i)=GP(j)+S1(i);
    end
end
S2 =round((S1*256)+0.5);
for i = 1:256
    GPeq(i) = sum(GP(find(S2 == i)));
    end
figure;
subplot(221);
bar(0:255,GP,'b');
title('原图像直方图') 
subplot(222);
bar(0:255,GPeq,'b')
title('均衡化后的直方图')
X = f;
for i = 0:255
    X(find(f==i)) = S2(i+1);
end
subplot(223);
imshow(f);
title('原图像');
subplot(224);
imshow(X);
title('直方图均衡化后的图像');

直方图规定化：
单映射规则SML
组映射规则GML？
咋算的？

四.空域滤波：模板处理

用像素及像素邻域组成的空间进行图像增强的方法

线性滤波——卷积

空域滤波器分类：

按照效果分：

平滑滤波器：消除噪声，减弱或消除图像中高频率分量
锐化滤波器:使图像反差增强，边缘明显，减弱或消除图像中的低频率分量

按运算性质分：

线性：卷积
非线性：逻辑运算，“卷积，算术，逻辑”的混合运算

高斯平滑滤波器

根据高斯概率分布来确定模板的各系数值

中值滤波器

非线性平滑滤波器

中值滤波器的主要功能就是让与周围像素灰度值的差比较大的像素改取与周围像素值接近的值，所以它对孤立的噪声像素的消除能力是很强的。由于它不是简单地取均值，因而产生的模糊比较少。换句话说，中值滤波器既能消除噪声又能保持图像的细节

（相比于均值滤波，中值滤波边缘轮廓比较清晰）

线性锐化滤波器

线性锐化滤波器的模板仅中心系数为正而周围的系数均为负值
在图像处理中一般限制图像的灰度值为正，所以卷积锐化后还需将输出图像灰度值范围通过变换变回到原图像的灰度范围

图像的梯度算子

1.sobel微分算子：

一阶导数最大值寻找边界
需要x方向图像就对y求微分，需要y方向图像就对x求微
分

在学习的时候看到这个写的不错，贴这儿
仔细看看，最好算算

2.拉普拉斯Laplacian算子:

利用二阶导数为0寻找边界

• 课后习题未做

频域图像增强

频域增强：通过改变图像中不同频率分量实现增强，而非逐个像素处理

卷积理论是频域技术的基础。设函数f(x, y)与线性位移不变算子h(x, y)的卷积结果是g(x, y)，即g(x, y) = h(x, y) * f(x, y)
那么根据卷积定理在频域有G(u, v)=H(u, v)F(u, v)，其中G(u, v)，H(u,v)，F(u, v)分别是g(x, y)，h(x, y)，f(x, y)的傅里叶变换。用线性系统理论的话来说，H(u, v)是**转移函数**
这样具有所需特性的g(x, y)就可得到：
g(x, y)=F–1[H(u, v)F(u, v)]
ps: u,v均为频率变量

1.傅里叶变换

傅里叶变换
（1）计算需增强图的傅里叶变换。
（2）将其与一个（根据需要设计的）转移函数相乘。（3）再将结果傅里叶反变换以得到增强的图。

2-D傅里叶变换

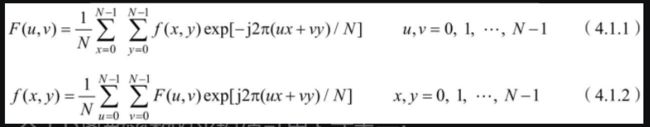
一个2-D离散函数的傅里叶变换在原点的值（零频率分量）与该函数的均值成正比

卷积定理指出：两个函数在空间的卷积与它们的傅里叶变换在频域的乘积构成一对变换，而两个函数在空间的乘积与它们的傅里叶变换在频域的卷积构成一对变换

相关定理指出：两个函数在空间的相关与它们的傅里叶变换（其中一个为其复共轭）在频域的乘积构成一对变换，而两个函数（其中一个为其复共轭）在空间的乘积与它们的傅里叶变换在频域的相关构成一对变换。即[插图]如果f(x)和g(x)是同一个函数，称为自相关；如果f(x)和g(x)不是同一个函数，称为互相关
？？？？？？没懂

f = imread('circuit.tif');
f = im2gray(f);
F1 = fft2(f);%傅里叶变换
F2 = fftshift(F1);%中心化
F1m = abs(F2);
F11 = log(F2);
figure;
imshow(uint8(F1m));

2.频域增强基本概念

图像的傅里叶变换用F(u, v)表示，滤波器的频域函数用H(u, v)表示，增强后图像的傅里叶变换用G(u, v)表示，则要实现低通滤波就需要选择一个合适的H(u, v)以得到能减弱F(u, v)高频分量的G(u, v)

3.低通滤波器——频域平滑

低频通过，高频衰减，用于减少尖锐的细节变化

理想低通滤波器 (ILPF)

		H(u,v) =  1, D(u,v)Do

D(u, v)是从点(u, v)到频率平面原点的距离，D(u, v)=(u2+v2)1/2
大于截止频率Do（D0是一个非负整数）为0，小于等于为1

会出现振铃效应

巴特沃斯低通滤波器（BLPF)

		H（u，v) = 1 / （1 + [D(u,v) / Do]^2n）

一阶无振铃，阶数越高振铃越明显

高斯低通滤波器（GLPF）

高斯低通滤波器没有振铃

4.高通滤波器——频域锐化

傅里叶变换中，低频主要决定图像在平滑区域中总体灰度级的显示，而高频决定图像细节部分，如边缘和噪声

高频通过，低频衰减
使图像更为锐化

滤波器函数：低通滤波器的反操作

	**H**hp(u,v) = 1 - **H**lp(u,v)

理想高通滤波器 (IHPF)

		H(u,v) =  0, D(u,v)Do

大于截止频率Do为1，小于等于为0

会出现振铃效应

巴特沃斯高通滤波器（BHPF)

		H（u，v) =1 / （1 + [ Do / D(u,v) ]^2n）

由于高低频率之间的过渡比较光滑，所以振铃效应不明显

高斯高通滤波器（GHPF）

特殊高通滤波器

高通增强滤波器

通过对频域里高通滤波器的转移函数加一个常数以将一部分（本要滤除的）低频分量加回到滤波结果中，从而获得较好的视觉效果
公式

高频提升滤波器

如果把原始图乘以一个放大系数A再减去低通图就可构成高频提升滤波器
公式

5.带通带阻与同态滤波器

带阻滤波器

组织一定频率范围内的信号通过，而允许其他频率范围内的信号通过
（像把一个带子阻拦在外面）

带通滤波器

（让这一个带子通过）

同态滤波器

一方面减弱图像中的低频分量（压缩了整体的动态范围），另一方面加强高频分量（增加了图像相邻各部分之间的对比度）

总结

空域技术与频域技术

空域	频域
平滑	低通
锐化	高通
平滑滤波器的模板函数的傅里叶变换	低通滤波器的转移函数
锐化滤波器的模板函数的傅里叶变换	高通滤波器的转移函数

以上就是今天学习的内容，本文介绍了一些重要概念，其中关于傅里叶变换，拉普拉斯算子，属于非常重要的内容，大概会在后续再专门写写！ 然后频域图像增强也很重要，后面的带通带阻的公式后续专门写写！并且理解！