Datawhale 李宏毅机器学习 Task2
Regression
- Regression
-
- 实践
Regression
就是找到一个函数 function ,通过输入特征 x,输出一个数值 Scalar。
-
Step1. Model
A set of function f 1 , f 2 , … f_1, f_2, \dots f1,f2,…- linear models : $ y = b + \sum w_ix_i $
- x i x_i xi: feature, $ w_i$: weight, b b b: bias
- linear models : $ y = b + \sum w_ix_i $
-
Step2. Goodness of Function
- Training Data
- Loss function L L L
- Input: a function
- Output: how bad it is
- $ L(f) = L(w, b) $
-
Step3. Best Function
- $ f^* = arg \min_f L(f) $
- Gradient Descent
- Model Selection
- overfitting
- Regularization: $ L = L + \lambda \sum (w_i)^2$
- 思考:为什么Regularization不需要加入bias?
实践
- 导入包
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
# matplotlib没有中文字体,动态解决
plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
- 传入数据
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
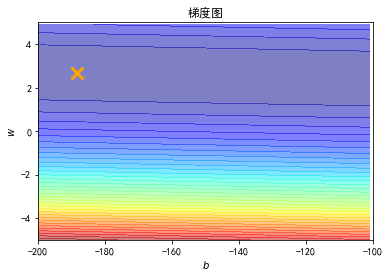
- 计算范围内各个值的loss值,绘制图形
# loss
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
Z[j][i] = 0 # meshgrid吐出结果:y为行,x为列
for n in range(len(x_data)):
Z[j][i] += (y_data[n] - b - w * x_data[n]) ** 2
Z[j][i] /= len(x_data)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("梯度图")
plt.show()
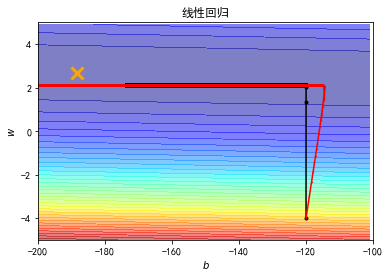
- 手动调整学习率
# linear regression
b = -120
w = -4
iteration = 100000
lr = 0.0000005
b_history = [b]
w_history = [w]
for i in range(iteration):
b_grad=0.0
w_grad=0.0
for n in range(len(x_data)):
b_grad=b_grad-2.0*(y_data[n]-n-w*x_data[n])*1.0
w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
b -= lr * b_grad
w -= lr * w_grad
b_history.append(b)
w_history.append(w)
- 根据 weight 和 bias 定制化学习率
# linear regression
b = -120
w = -4
iteration = 100000
lr = 1
lr_b=0
lr_w=0
b1_history = [b]
w1_history = [w]
for i in range(iteration):
b_grad=0.0
w_grad=0.0
for n in range(len(x_data)):
b_grad=b_grad-2.0*(y_data[n]-n-w*x_data[n])*1.0
w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
lr_b=lr_b+b_grad**2 # 定制化学习率
lr_w=lr_w+w_grad**2 # 定制化学习率
# update param
b -= lr/np.sqrt(lr_b) * b_grad
w -= lr /np.sqrt(lr_w) * w_grad
b1_history.append(b)
w1_history.append(w)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.plot(b1_history, w1_history, 'o-', ms=0.5, lw=1.5, color='red')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()