深度学习入门之从感知机到神经网络

前言

前文介绍了感知机，感知机的优点是即使是非常复杂的函数，感知机也能隐式的表示，但是每一层的权重都是由人工确定，在非常复杂的模型中，这无疑是致命的，因此，产生了神经网络。

---

一、神经网络

1.1 神经网络基本模型

• 隐藏层也叫隐层，中间层

1.2 激活函数的由来

1.2.1 回顾感知机

$$y=\{\begin{array}{l}0,w_1{x}_1+w_2{x}_2+b\le 0\\ 1,w_1{x}_1+w_2{x}_2+b>0\end{array}$$
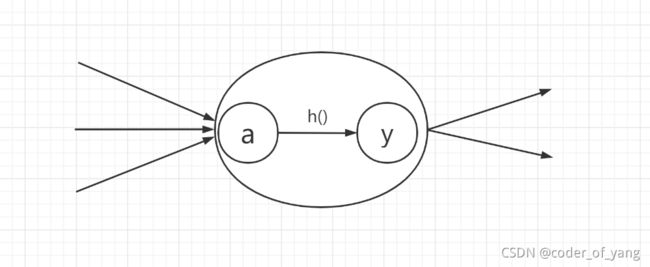
偏置b在上图并没有给出，这里，为了简洁，我们用函数h(x)表示这种分情况的行为

$$y=h(x)=\{\begin{array}{l}0,x\le 0\\ 1,x>0\end{array}$$

这里的h(x)函数会将输入信号转化为输出信号，这样的函数称为激活函数（activation function），激活函数的作用在于如何来激活输入信号的总和。

用a来表示输入信号的总和，那么这一过程可描述如下图

1.3常见激活函数

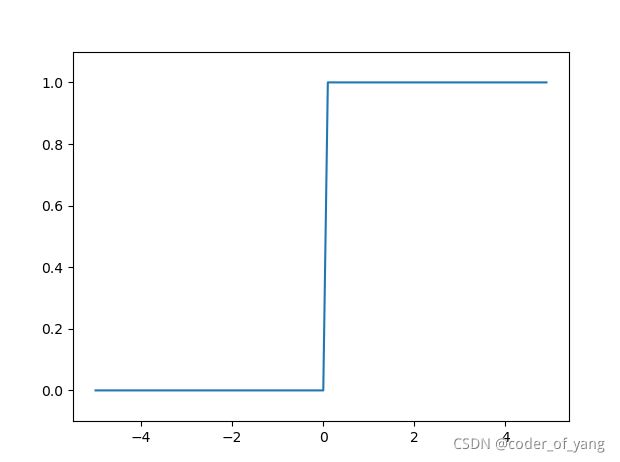
1.3.1 阶跃函数

像上面介绍的，当超过某个值时（也称阈值），就切换输出的激活函数称为阶跃函数

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def step_function(x):
    return np.array(x > 0, dtype=np.int)

X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)  # 指定图中绘制的y轴的范围
plt.show()

可以看出阶跃函数的变化是急剧性的，下面看下常用的sigmoid函数

1.3.2 sigmoid函数

$$h(x)=\begin{array}{r}\frac{1}{1+e^{(-x)}}\end{array}$$

神经网络区别感知机的最大不同就是参数是自己学习的，另一区别就是激活函数的不同

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))    

X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()

sigmoid函数也叫Logistic函数，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。

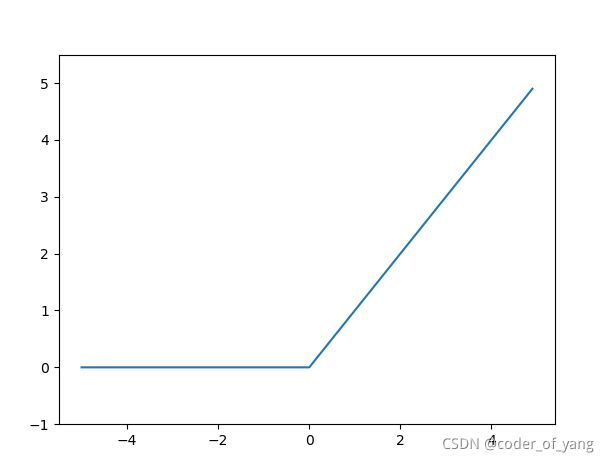
1.3.3 Relu函数

$$h(x)=\{\begin{array}{l}0,x\le 0\\ x,x>0\end{array}$$

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()

Relu函数看上区非常的简单，作为线性函数的鼻祖，Relu具有非常多的变种，广泛应用于神经网络的学习，如带泄露线性整流(Leaky ReLU)， 带泄露随机线性整流(Randomized Leaky ReLU)，以及噪声线性整流(Noisy ReLU)。

总结

本文主要介绍感知机到神经网络的过程以及激活函数的由来和常用激活函数，下节将写到损失函数的由来以及梯度