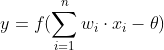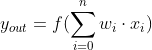深度学习入门——感知机（学习笔记）

目录

感知机概念

感知机学习过程和权值更新规则

多层感知机

感知机案例代码

---

感知机概念

       首先我们需要大致了解生物神经元的工作流程，在生物神经网络中，每个神经元与其他神经元通过突触进行连接。神经元之间的信息传递，属于化学物质的传递。当它兴奋时，就会向与它相连的神经元发送化学物质，从而改变这些神经元的电位。如果某些神经元的电位超过了一个阈值，那么它就会被激活，接着向其他神经元发送化学物质，如此进行层层传播。

        感知机模拟生物神经元的工作流程，通过设置各个神经元的某种连接权重，将神经元接收到的所有输入值按照权重叠加起来，再与当前神经元的阈值进行比较（我理解的阈值是一个临界值，代表了可以上下波动的幅度），最终通过激活函数向外表达输出。其模型可以用以下公式表示（为第i个神经元的输入，为第i个神经元的连接权重，为阈值，f为激活函数，y是最终输出）：

   

       神经元之间的连接权重大小代表了连接的强弱，其实是希望获得不同关注重点的信息。阈值也被称为偏置，表示神经元是否更容易被激活。神经元的工作模型存在激活和抑制两种状态的跳变，所以理想的激活函数是阶跃函数（实际使用中常用sigmoid函数来代替阶跃函数，因为阶跃函数不光滑、不连续，不便于求导、寻找极值）。感知机中激活函数使用的是阶跃函数，这里可以理解为当刺激强度（加权和）大于等于该神经元的阈值时，该神经元表现为兴奋状态，输出y=1;反之则表现出抑制状态，输出y=0。

        感知机最初并不知道正确的权重应该是多少，在一开始只是设置一个随机值，然后根据训练数据计算得到输出，再通过计算误差（实际值与输出值之差）来调整权重，使其修改后计算的误差减小，最终使得输入的每个数据都能计算出正确的结果，这就是感知机的学习过程。所谓的神经网络的学习规则，就是调整神经元之间的连接权值和神经元内部阈值的规则。感知机是一种简单的二分类的线性分类模型（二分类中，一般用y=1表示一类，用y=0表示另一类），对于输入数据是二维的，感知机的几何意义是找一条直线将表示输入数据的平面中的点分开；那么如果输入数据是三个维度的，则相当于找到一个平面，在三维空间中将它们分成两类；对于更高维度的数据，就是寻找对应的超平面。该平面和超平面方程都是由权值参数来确定的。

感知机学习过程和权值更新规则

第一步，随机初始化权值,为了统一描述，用代替 （即代替阈值）。 

第二步，输入一个样本和对应的期望结果y。

第三步，激活函数加工后的感知机输出结果：

第四步，计算误差，以误差为基础对每个权值，按以下规则进行调整（称为学习率，是一个人为设置的常量，一般在 0-1 之间，用来控制每次权重的调整力度。它本身的值是比较难确定的，依赖于人工的经验（属于超参数范畴），如果太小，网络调参的次数较多，收敛会很慢；如果太大，会错过参数的最优解。一般将其初始值设置为一个较小的值，如0.1）：

第五步，循环以上步骤，对所有样本进行训练，直到训练一定轮数或者误差达到最小时停止。

注：

1. 在使用感知机实现分类问题时，根据某个样本的误差，对权值进行调整时，可能引起其他原本分类正确的样本出错。所以每次调整之后，要把所有样本都重新计算一遍。

2. 为了减小每个样本由于误差不同而进行多次调整的问题，可以把所有样本的误差求和，然后再对权值进行一次调整，实现每次调整让总体误差最小。

3. 能线性分割不同样本的直线非常多，根据初始参数和学习率，最终得到的权值参数结果并不唯一。

4. 感知机旨在通过最小化误差，来优化分类超平面，从而达到对新实例实现准确预测。而由于感知机只有输出层神经元可以进行激活函数的处理，即它只拥有单层的神经元，因此它的学习能力是相对有限的。如果这些样本本身不是用一条直线可以分割的（即非线性可分），那么这个学习过程就无法终止。因此，感知机无法解决线性不可分问题。

多层感知机

        随着研究的进行，人们发现在输入层与输出层之间增加隐含层，构成一种多层神经网络结构，每一层神经元仅与下一层的神经元全连接在同一层之内，神经元彼此不连接，而且跨层之间的神经元，彼此也不相连。这样的结构可以解决非线性分类的问题，增强感知机的分类能力，这就是多层感知机（输入层不算入神经网络层次，且隐含层和输出层中的神经元都拥有激活函数）。

       由于当时感知机只给出了最后一层神经元权值的训练方法，所以其他层的参数则只能人为设置。单层感知机能够根据已知数据来学习参数，在线性可分的问题领域具有很好的效果，但它不能处理线性不可分问题。而多层感知机只能训练最后一层参数， 实用性有限。反向传播算法（即BP 算法）的提出，使得多层神经网络的训练变得简单可行，证明了多层神经网络具有很强的学习能力。从而将神经网络的研究推向了新的高潮（BP 算法将会在下一篇学习笔记中涉及）。

感知机案例代码

import matplotlib.pyplot as plt


# 声明了一个感知机类Perception
class Perception():
    # input_para_num输入参数个数 acti_func激活函数
    def __init__(self, input_para_num, acti_func):
        self.activator = acti_func
        # 权重向量初始化
        self.weights = [-1, 1, 1]

    # 针对每个输入向量，输出感知机的计算结果
    def predict(self, row_vec):
        act_values = 0.0
        for i in range(len(self.weights)):
            act_values += self.weights[i]*row_vec[i]
        return self.activator(act_values)

    # 训练权值参数 dataset一组向量、与每个向量对应的label iteration指定迭代次数 rate学习率
    def train(self, dataset, iteration, rate):
        weight = "["
        for i in range(iteration):
            for input_vec_label in dataset:
                # 计算感知机在当前权重下的输出
                prediction = self.predict(input_vec_label)
                print("输出", prediction)
                # 更新权重
                self._update_weights(input_vec_label, prediction, rate)
                weight = weight+str(self.weights)+","
        return weight.strip(",")+"]"

    # 更新权重
    def _update_weights(self, input_vec_label, prediction,rate):
        delta = input_vec_label[-1]-prediction
        print("误差", delta)
        for i in range(len(self.weights)):
            self.weights[i] += rate*delta*input_vec_label[i]
        print("权重", self.weights)


# 定义激活函数f
def func_activator(input_value):
    return 1.0 if input_value >= 0.0 else 0.0


def polt(dataset, i, weight):
    x1, y1, x2, y2, xx, yy = [], [], [], [], [], []
    for row in dataset:
        if row[-1] == 1:
            x1.append(row[1])
            y1.append(row[2])
        if row[-1] == 0:
            x2.append(row[1])
            y2.append(row[2])
    # 设置字体样式
    plt.rcParams['font.family'] = ['sans-serif']
    # 设置字体显示中文
    plt.rcParams['font.sans-serif'] = ['SimHei']
    # 设置绘图的坐标范围
    plt.axis([0, 2, 0, 2])
    # bs是blue squares蓝色方块缩写
    # ro红色圆点 b-蓝色线条 g^绿色三角形
    plt.plot(x1, y1, 'rs', label='原始数据(类别1)')
    plt.plot(x2, y2, 'bs', label='原始数据(类别0)')
    xx.append(0.1)
    xx.append(1.1)
    yy.append((-weight[i][1]*0.1-weight[i][0])/weight[i][2])
    yy.append((-weight[i][1]*1.1-weight[i][0])/weight[i][2])
    plt.plot(xx, yy, 'r', linewidth=2, label='拟合直线')
    # 显示网格线
    plt.grid()
    # 显示图中标签
    plt.legend()
    plt.show()


def get_training_dataset():
    # 构建训练数据
    dataset = [[1, 0.1, 1, 1], [1, 0.2, 0.7, 1], [1, 0.4, 0.8, 1],
               [1, 0.8, 0.3, 0], [1, 0.9, 0.2, 0], [1, 1.0, 0.5, 0],
               [1, 0.1, 1, 1]]
    return dataset


def train_and_perceptron():
    # 创建感知器，输入参数个数为3（虽然是二元函数，把哑元-1算上，是三个），激活函数为func_activator
    p = Perception(3, func_activator)
    # 获取训练数据，迭代1轮, 学习速率为0.6
    dataset = get_training_dataset()
    weight = p.train(dataset, 1, 0.6)
    for i in range(len(dataset)):
        polt(dataset, i, eval(weight))
    # 返回训练好的感知机
    return p


if __name__ == '__main__':
    and_perception = train_and_perceptron()

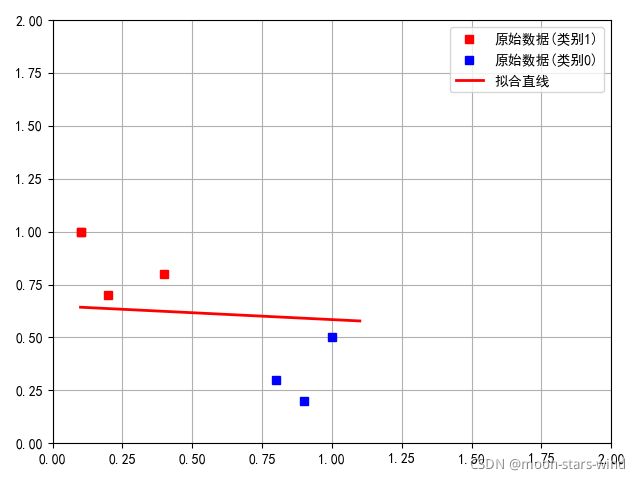
分类结果图示：

 注：如有问题，欢迎批评指正！

（本文参考书目：深度学习之美、人工智能概论）