python实现机器学习算法——K均值聚类算法
文章目录
- 1.序言
- 2.K均值算法
-
- 2.1简介
- 2.2算法过程
- 3.实现代码
-
- 主函数
- 导入数据集
- 初始化聚类中心
- 样本聚类
- 更新聚类中心
- 判断是否更新
- 绘制效果图
- 代码整合
1.序言
本人是一名刚升大二的学生,最近刚接触机器学习,当学到这些算法以后就想试试用自己现有的能力来实现他们,我选择了相对容易理解的K均值聚类算法进行实现,相信很多小伙伴也都有过这种想法,所以决定将我实现算法的过程和代码分享出来,这也是我第一次写博客,希望能给跟我一样正在学习的同学带来帮助,同时也欢迎各路前辈提出优化方案和意见。
2.K均值算法
2.1简介
k均值算法是机器学习中一个经典的分类算法,通过设立中心点,将与之最近的样本归为一类,从而达到分类的效果,再不停地利用均值计算新的中心点,反复如此,直至达到最佳的分类效果。
如图则是实现效果
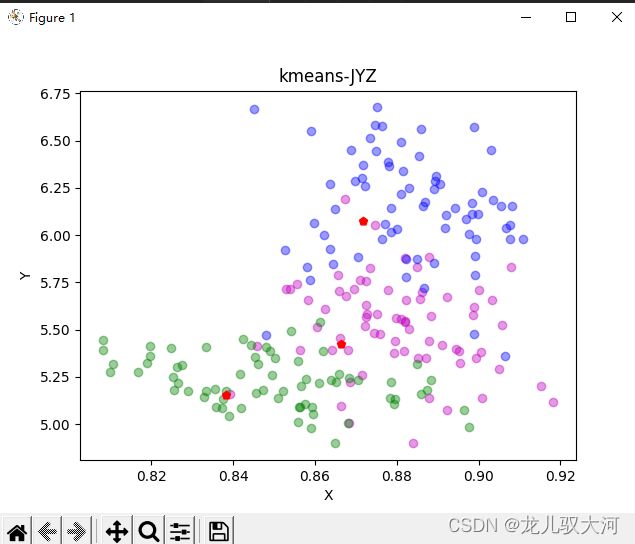
2.2算法过程
想要实现一个算法,了解它的具体流程和原理是必须的,所以在实现之前先了解一下此算法是如何运行的.
第一步:初始化聚类中心在运行整个算法前,需要有一组中心点来作为最初中心点,以便在此基础上进行更新,初始化中心点可以是随机的,具体方法将在代码中讲解
第二步:根据中心点对样本进行分类计算样本与每个中心点的距离,将该样本分给离它最近的中心点那一类,当所有样本计算完后即完成了算法的第一次分类
第三步:计算新的聚类中心因为第二步已经分好了类,现在只用对每个类中的所有样本求均值,将得到的均值作为该类别新的聚类中心
第四步:比较前后聚类中心这里比较前后的聚类中心是为了了解中心点的变化情况以判断是否需要继续更新,刚开始的变化也许会很大,通过不停的重复更新,中心点的前后变化会越来越小,这里我们就可以设定一个程度,当变化程度小于我们设定的程度时,我们就可以认为当前的聚类中心不需要再更新
注:若需要更新中心点,则需要重新进行第二到第四步,直至不需要更新后方可进行第五步
第五步:绘制聚类效果图通过绘制效果图可以更直观地判断自己的的分类个数和设定程度是否合适
以上则是算法实现的大致流程,接下来就来看看用代码将如何对算法进行实现
3.实现代码
主函数
主函数的内容与2.2中的算法过程基本一致就不做过多叙述
if __name__ == '__main__':
k = 3
print("第一步:调用数据集")
sample_data = load_data(file_path="E:\\pythonproject\\clustering-algorethm\\data")
print("第二步:初始化聚类中心")
old_cluster_center = initialize_cluster_center(data=sample_data, k=k)
print("初始化聚类中心如下")
print(old_cluster_center)
print("第三步:聚类并更新中心点")
center_update_pro = center_update()
c = np.shape(sample_data)[1]
true_center = np.mat(np.zeros((k,c)))
count = 0
while True:
#聚类结果
collect_result = center_update_pro.collect(data=sample_data, old_center=old_cluster_center, k=k)
print("聚类结果如下")
print(collect_result)
#计算新的聚类中心
new_cluster_center = center_update_pro.new_point_calculate(collect_result)
#判断是否继续更新
result = center_update_pro.change_judge(last_point=old_cluster_center, now_point=new_cluster_center)
if result == 1:
count += 1
print(f"更新 {count} 次后完成更新")
print("保存最终聚类中心点")
true_center = new_cluster_center
print(f"如下为最终中心点{true_center}")
np.savetxt("E:\\pythonproject\\clustering-algorethm\\finish_data.txt" ,np.c_[collect_result])
print(collect_result)
print("绘制聚类效果图")
center_update_pro.draw( sample_data,true_center, collect_result )
break
else:
#新旧中心点更替
old_cluster_center = new_cluster_center
count += 1
print(f"更新 {count} 次")
continue
导入数据集
该算法用于数据的分类,所以首先要导入准备好的数据集,本章的数据样本来源于UCI上的小麦种子数据集。
#调用数据集
def load_data(file_path):
f = open(file_path)
data = []
for line in f.readlines():
row = []
lines = line.strip().split()
for i in lines:
row.append(float(i))
data.append(row)
f.close()
return np.mat(data)
这里将数据集以矩阵的形式保存是为了后续能利用矩阵的运算规则更方便的进行计算
初始化聚类中心
#初始化聚类中心
def initialize_cluster_center(data , k):
sum = np.shape(data)[1]
my_center = np.mat(np.zeros((k,sum)))#生成零矩阵储存聚类中心信息
for i in range(sum): # 遍历每一个特征,在每个特征上取一个最大值与最小值之间的随机值
xmin = np.min(data[:, i])
xrange = np.max(data[:, i]) - xmin
my_center[:, i] = xmin*np.mat(np.ones((k,1))) + np.random.rand(k, 1) * xrange
return my_center
初始化的方法是遍历每一个特征的所有样本,分别得到每个特征的最大值和最小值,以二者之差作为变化范围,用最小值加上一个0-1的随机值与最大值的乘积方可得到最小值与最大值之间的一个随机值来作为初始值,每个特征均如此便可成功初始化聚类中心
样本聚类
本章分类中所用距离为欧氏距离
![]()
这里将数据分为三部分拼接是为了方便在后续操作中方便分出哪些属于哪个类别
def collect(self , data , old_center,k):#聚类
m, n = np.shape(data) # m为样本个数,n为特征个数
label_1 = np.mat(np.zeros((n)))
label_2 = np.mat(np.zeros((n)))
label_3 = np.mat(np.zeros((n))) # 创造三个零矩阵用于储存分类结果
for i in range(m): # 遍历样本
label = 0
min_distance = np.inf#初始化最小距离为正无穷
for j in range(k): # 分别计算此样本与各个中心的距离并找出最小值
distance = np.power(data[i,] - old_center[j,], 2).sum()
distance = math.sqrt(distance)
if distance < min_distance:
min_distance = distance
label = j + 1
if label == 1:
label_1 = np.row_stack((label_1, data[i, :]))
if label == 2:
label_2 = np.row_stack((label_2, data[i, :]))
if label == 3:
label_3 = np.row_stack((label_3, data[i, :])) # 根据类型填入相应矩阵
# 在每个样本最后加一个类别元素,以方便计算新的聚类中心时将各组分开
label_1 = np.delete(label_1, 0, axis=0)
oth_1 = np.mat(np.ones((np.shape(label_1)[0],1)))
label_1 = np.column_stack((label_1 , oth_1))
label_2 = np.delete(label_2, 0, axis=0)
oth_2 = np.mat(np.ones((np.shape(label_2)[0],1)))*2
label_2 = np.column_stack((label_2 , oth_2))
label_3 = np.delete(label_3, 0, axis=0)
oth_3 = np.mat(np.ones((np.shape(label_3)[0],1)))*3
label_3 = np.column_stack((label_3 , oth_3))
label = np.row_stack((label_1, label_2, label_3))#将三个类垂直拼接为一个矩阵返回
return label
更新聚类中心
获得聚类样本后便通过均值计算新的聚类中心
def new_point_calculate(self, data):
m, n = np.shape(data)
label_1 = np.mat(np.zeros((n)))
label_2 = np.mat(np.zeros((n)))
label_3 = np.mat(np.zeros((n)))#用于放置各类样本
for l in range(m):#分类放置
if data[l,-1] == 1:
label_1 = np.row_stack((label_1, data[l, :]))#将该样本放入对应矩阵
if data[l,-1] == 2:
label_2 = np.row_stack((label_2, data[l, :]))
if data[l,-1] == 3:
label_3 = np.row_stack((label_3, data[l, :]))
#删除类别元素,恢复矩阵格式
label_1 = np.delete(label_1, -1, axis=1)
label_2 = np.delete(label_2, -1, axis=1)
label_3 = np.delete(label_3, -1, axis=1)
m1,n1 = np.shape(label_1)
m2,n2 = np.shape(label_2)
m3,n3 = np.shape(label_3)
center_1 = np.mat(np.zeros((1,n1)))
center_2 = np.mat(np.zeros((1,n2)))
center_3 = np.mat(np.zeros((1,n3)))
for i in range(n1):
sum_1 = label_1[:,i].sum()/m1
center_1[0,i] = sum_1#计算中心点1的第i个特征
for i in range(n2):
sum_2 = label_2[:,i].sum()/m2
center_2[0,i] = sum_2
for i in range(n3):
sum_3 = label_3[:,i].sum()/m3
center_3[0,i] = sum_3
new_point = np.row_stack((center_1, center_2, center_3))
return new_point
判断是否更新
本章判断更新是以前后几个中心的欧式距离的平均值来作为判断依据,可以通过更改代码中最后一个if条件来调整变化范围
def change_judge(self, last_point, now_point):#判断是否继续更新中心
m,n = np.shape(last_point)
distance = 0
for i in range(m):#计算第i个中心的距离
distance += np.power(last_point[i,:] - now_point[i,:], 2).sum()
distance += math.sqrt(distance)
distance = distance/m #m个中心点前后距离差的平均值作为中心点变化的整体变化距离
if distance < 0.05:#通过调整该值来设置中心点最低变化距离
return 1#完成
else:
return 0#未完成
绘制效果图
调用matplotlib中的scatter函数进行绘制
def draw(self,point_data, center, sub_center):
Myfig = plt.figure()
axes = Myfig.add_subplot(111)
length = len(point_data)
print(length)
for a in range(length):
if sub_center[a, -1] == 1:
axes.scatter(point_data[a, 2], point_data[a, 3], color='m', alpha=0.4)
if sub_center[a, -1] == 2:
axes.scatter(point_data[a, 2], point_data[a, 3], color='b', alpha=0.4)
if sub_center[a, -1] == 3:
axes.scatter(point_data[a, 2], point_data[a, 3], color='g', alpha=0.4)
for i in range(len(center)):
axes.scatter(center[i, 2], center[i, 3], color='red', marker='p')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('kmeans-JYZ')
plt.show()
代码整合
import matplotlib.pyplot as plt
import numpy as np
import math
#调用数据集
def load_data(file_path):
f = open(file_path)
data = []
for line in f.readlines():
row = []
lines = line.strip().split()
for i in lines:
row.append(float(i))
data.append(row)
f.close()
return np.mat(data)
#初始化聚类中心
def initialize_cluster_center(data , k):
sum = np.shape(data)[1]
my_center = np.mat(np.zeros((k,sum)))#生成零矩阵储存聚类中心信息
for i in range(sum): # 遍历每一个特征,在每个特征上取一个最大值与最小值之间的随机值
xmin = np.min(data[:, i])
xrange = np.max(data[:, i]) - xmin
my_center[:, i] = xmin*np.mat(np.ones((k,1))) + np.random.rand(k, 1) * xrange
return my_center
class center_update(object):#创造中心点更新类
def draw(self,point_data, center, sub_center):
Myfig = plt.figure()
axes = Myfig.add_subplot(111)
length = len(point_data)
print(length)
for a in range(length):
if sub_center[a, -1] == 1:
axes.scatter(point_data[a, 2], point_data[a, 3], color='m', alpha=0.4)
if sub_center[a, -1] == 2:
axes.scatter(point_data[a, 2], point_data[a, 3], color='b', alpha=0.4)
if sub_center[a, -1] == 3:
axes.scatter(point_data[a, 2], point_data[a, 3], color='g', alpha=0.4)
for i in range(len(center)):
axes.scatter(center[i, 2], center[i, 3], color='red', marker='p')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('kmeans-JYZ')
plt.show()
def change_judge(self, last_point, now_point):#判断是否继续更新中心
m,n = np.shape(last_point)
distance = 0
for i in range(m):#计算第i个中心的距离
distance += np.power(last_point[i,:] - now_point[i,:], 2).sum()
distance += math.sqrt(distance)
distance = distance/m#m个中心点前后距离差的平均值作为中心点变化的整体变化距离
if distance < 0.05:#通过调整该值来设置中心点最低变化距离
return 1#完成
else:
return 0#未完成
def new_point_calculate(self, data):
m, n = np.shape(data)
label_1 = np.mat(np.zeros((n)))
label_2 = np.mat(np.zeros((n)))
label_3 = np.mat(np.zeros((n)))#用于放置各类样本
for l in range(m):#分类放置
if data[l,-1] == 1:
label_1 = np.row_stack((label_1, data[l, :]))#将该样本放入对应矩阵
if data[l,-1] == 2:
label_2 = np.row_stack((label_2, data[l, :]))
if data[l,-1] == 3:
label_3 = np.row_stack((label_3, data[l, :]))
#删除类别元素,恢复矩阵格式
label_1 = np.delete(label_1, -1, axis=1)
label_2 = np.delete(label_2, -1, axis=1)
label_3 = np.delete(label_3, -1, axis=1)
m1,n1 = np.shape(label_1)
m2,n2 = np.shape(label_2)
m3,n3 = np.shape(label_3)
center_1 = np.mat(np.zeros((1,n1)))
center_2 = np.mat(np.zeros((1,n2)))
center_3 = np.mat(np.zeros((1,n3)))
for i in range(n1):
sum_1 = label_1[:,i].sum()/m1
center_1[0,i] = sum_1#计算中心点1的第i个特征
for i in range(n2):
sum_2 = label_2[:,i].sum()/m2
center_2[0,i] = sum_2
for i in range(n3):
sum_3 = label_3[:,i].sum()/m3
center_3[0,i] = sum_3
new_point = np.row_stack((center_1, center_2, center_3))
return new_point
def collect(self , data , old_center,k):#聚类
m, n = np.shape(data) # m为样本个数,n为特征个数
label_1 = np.mat(np.zeros((n)))
label_2 = np.mat(np.zeros((n)))
label_3 = np.mat(np.zeros((n))) # 创造三个零矩阵用于储存分类结果
for i in range(m): # 遍历样本
label = 0
min_distance = np.inf#初始化最小距离为正无穷
for j in range(k): # 分别计算此样本与各个中心的距离并找出最小值
distance = np.power(data[i,] - old_center[j,], 2).sum()
distance = math.sqrt(distance)
if distance < min_distance:
min_distance = distance
label = j + 1
if label == 1:
label_1 = np.row_stack((label_1, data[i, :]))
if label == 2:
label_2 = np.row_stack((label_2, data[i, :]))
if label == 3:
label_3 = np.row_stack((label_3, data[i, :])) # 根据类型填入相应矩阵
# 在每个样本最后加一个类别元素,以方便计算新的聚类中心时将各组分开
label_1 = np.delete(label_1, 0, axis=0)
oth_1 = np.mat(np.ones((np.shape(label_1)[0],1)))
label_1 = np.column_stack((label_1 , oth_1))
label_2 = np.delete(label_2, 0, axis=0)
oth_2 = np.mat(np.ones((np.shape(label_2)[0],1)))*2
label_2 = np.column_stack((label_2 , oth_2))
label_3 = np.delete(label_3, 0, axis=0)
oth_3 = np.mat(np.ones((np.shape(label_3)[0],1)))*3
label_3 = np.column_stack((label_3 , oth_3))
label = np.row_stack((label_1, label_2, label_3))#将三个类垂直拼接为一个矩阵返回
return label
if __name__ == '__main__':
k = 3
print("第一步:调用数据集")
sample_data = load_data(file_path="E:\\pythonproject\\clustering-algorethm\\data")
print("第二步:初始化聚类中心")
old_cluster_center = initialize_cluster_center(data=sample_data, k=k)
print("初始化聚类中心如下")
print(old_cluster_center)
print("第三步:聚类并更新中心点")
center_update_pro = center_update()
c = np.shape(sample_data)[1]
true_center = np.mat(np.zeros((k,c)))
count = 0
while True:
#聚类结果
collect_result = center_update_pro.collect(data=sample_data, old_center=old_cluster_center, k=k)
print("聚类结果如下")
print(collect_result)
#计算新的聚类中心
new_cluster_center = center_update_pro.new_point_calculate(collect_result)
#判断是否继续更新
result = center_update_pro.change_judge(last_point=old_cluster_center, now_point=new_cluster_center)
if result == 1:
count += 1
print(f"更新 {count} 次后完成更新")
print("保存最终聚类中心点")
true_center = new_cluster_center
print(f"如下为最终中心点{true_center}")
np.savetxt("E:\\pythonproject\\clustering-algorethm\\finish_data.txt" ,np.c_[collect_result])
print(collect_result)
print("绘制聚类效果图")
# center_update_pro.draw(data = collect_result , center = true_center)
center_update_pro.draw( sample_data,true_center, collect_result )
break
else:
#新旧中心点更替
old_cluster_center = new_cluster_center
count += 1
print(f"更新 {count} 次")
continue
以上便是我这次实现算法的全部过程,欢迎指导。
初始化思路借鉴于 https://blog.csdn.net/weixin_41744192/article/details/113736788
绘制图像借鉴于https://blog.csdn.net/weixin_41744192/article/details/113736788