Python机器学习之k-means聚类算法

1 引言

所谓聚类,就是按照某个特定的标准将一个数据集划分成不同的多个类或者簇,使得同一个簇内的数据对象的相似性尽可能大,同时不再一个簇内的数据对象的差异性也尽可能大,聚类算法属于无监督学习算法的一种.

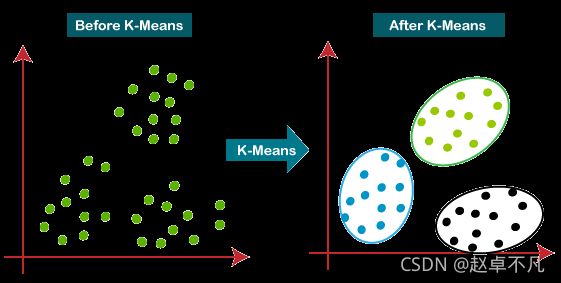
k-均值聚类的目的是：把 n个点（可以是样本的一次观察或一个实例)划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准。

2 K-Means

k-均值聚类算法属于最基础的聚类算法,该算法是一种迭代的算法,将规模为n的数据集基于数据间的相似性以及距离簇内中心点的距离划分成k簇.这里的k通常是由用户自己指定的簇的个数,也就是我们聚类的类别个数.

该算法的一般步骤如下:

• step1 选择k,来指定我们需要聚类的类别数目.参考上图a,这里k=2.
• step2 从数据集中随机选择k个样本作为我们不同类别的类内的中心点.参考图b中红色和蓝色x字
• step3 对数据集中的每一个样本,计算该样本到k个中心点的距离,选择距离该样本最近的中心点的类别作为该样本的类别.参考上图c.
• step4 根据上一步重新指定的样本的类别,计算每个类别的类内中心点.图d所示,重新计算的类内中心点为红色和蓝色x字.
• step5 重复步骤3,为数据集中的每个样本重新分配距离其最近的中心点的类别.图e所示.
• step6 如果给每个样本分配的类别发生改变,则进入step4,否则进入step7
• step7 算法结束.图f所示.

3 K值确定

通过上述描述,我们基本理解了k-means算法工作的原理,但是遗留给我们的问题是这个k值要如何确定呢?由于这个值是算法的输入,需要用户自行指定,当然不可以随便拍脑袋想了.这里介绍一种常用的WCSS方法来进行k值的选择.

WCSS算法是Within-Cluster-Sum-of-Squares的简称,中文翻译为最小簇内节点平方偏差之和.白话就是我们每选择一个k,进行k-means后就可以计算每个样本到簇内中心点的距离偏差之和, 我们希望聚类后的效果是对每个样本距离其簇内中心点的距离最小,基于此我们选择k值的步骤如下:

• step1 选择不同的k值(比如1-14),对数据样本执行k-means算法
• step2 对于每个k值,计算相应的WCSS值
• step3 画出WCSS值随着k值变化的曲线
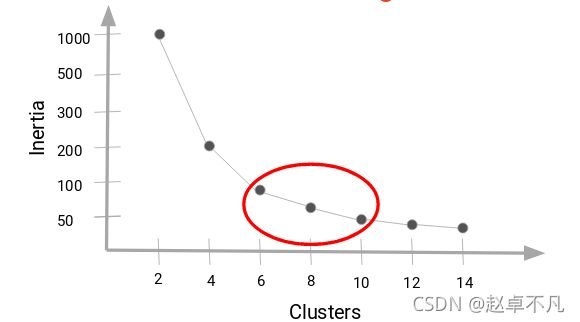
• step4 一般来说WCSS值应该随着K的增加而减小，然后趋于平缓，选择当WCSS开始趋于平衡时的K的取值.上图中可以选择6-10之间的值作为k值.

4 代码实现

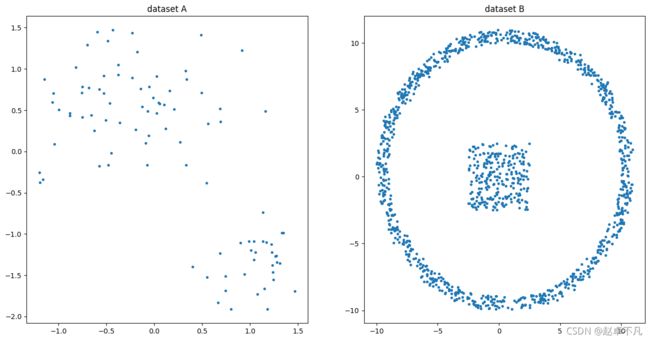
4.1 样例数据分布

我们使用python生成我们的数据代码如下:

from clustering__utils import *
x1, y1, x2, y2 = synthData()
X1 = np.array([x1, y1]).T
X2 = np.array([x2, y2]).T

结果如下:

4.2 实现K-means

参考上述原理,我们来实现kMeans,我们将其封装成类,代码如下:

class kMeans(Distance):
    def __init__(self, K=2, iters=16, seed=1):
        super(kMeans, self).__init__()
        self._K = K
        self._iters = iters
        self._seed = seed
        self._C = None
    
    def _FNC(self, x, c, n):
        # for each point,
        # find the nearest center
        cmp = np.ndarray(n, dtype=int)
        for i, p in enumerate(x):
            d = self.distance(p, self._C)
            cmp[i] = np.argmin(d)
        return cmp
    
    def pred(self, X):
        # prediction
        n, dim = X.shape
        np.random.seed(self._seed)
        sel = np.random.randint(0, n, self._K)
        self._C = X[sel]
        cmp = self._FNC(X, self._C, n)
        for _ in range(self._iters):
            # adjust position of centroids
            # to the mean value
            for i in range(sel.size):
                P = X[cmp == i]
                self._C[i] = np.mean(P, axis=0)
            cmp = self._FNC(X, self._C, n)
        return cmp, self._C

上述代码中:

• FNC函数中x为输入样本,c为聚类中心点,n为样本数目,该函数为每个样本计算其最近的中心点
• pred函数首先重新计算样本中心点,然后基于此给样本数据重新分配所属类别.返回值为n个样本所属中心点以及中心点的位置.

4.3 确定k

我们使用以下代码,计算不同k值下的WCSS的值

# elbow method
Cs = 12
V1 = np.zeros(Cs)
V2 = np.zeros(Cs)
D = Distance()
for k in range(Cs):
    kmeans = kMeans(K=k + 1, seed=6)
    fnc1, C1 = kmeans.pred(X1)
    fnc2, C2 = kmeans.pred(X2)
    for i, [c1, c2] in enumerate(zip(C1, C2)):
        d1 = D.distance(c1, X1[fnc1 == i])**2
        d2 = D.distance(c2, X2[fnc2 == i])**2
        V1[k] += np.sum(d1)
        V2[k] += np.sum(d2)

结果如下:
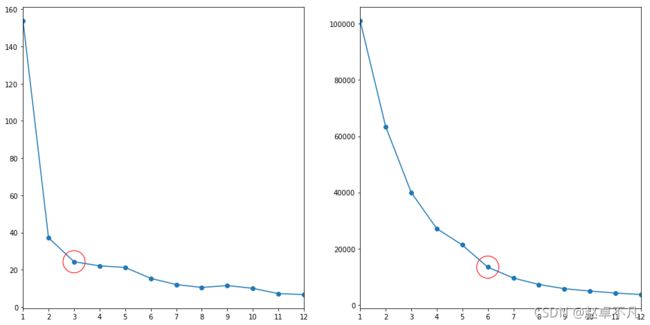这里我们对第一组数据,选择k=3,针对第二组数据选择k=6,示例如上图红色圆圈所示.

4.4 最终效果

我们根据上述选定的k值,可视化两组数据迭代过程,代码如下:

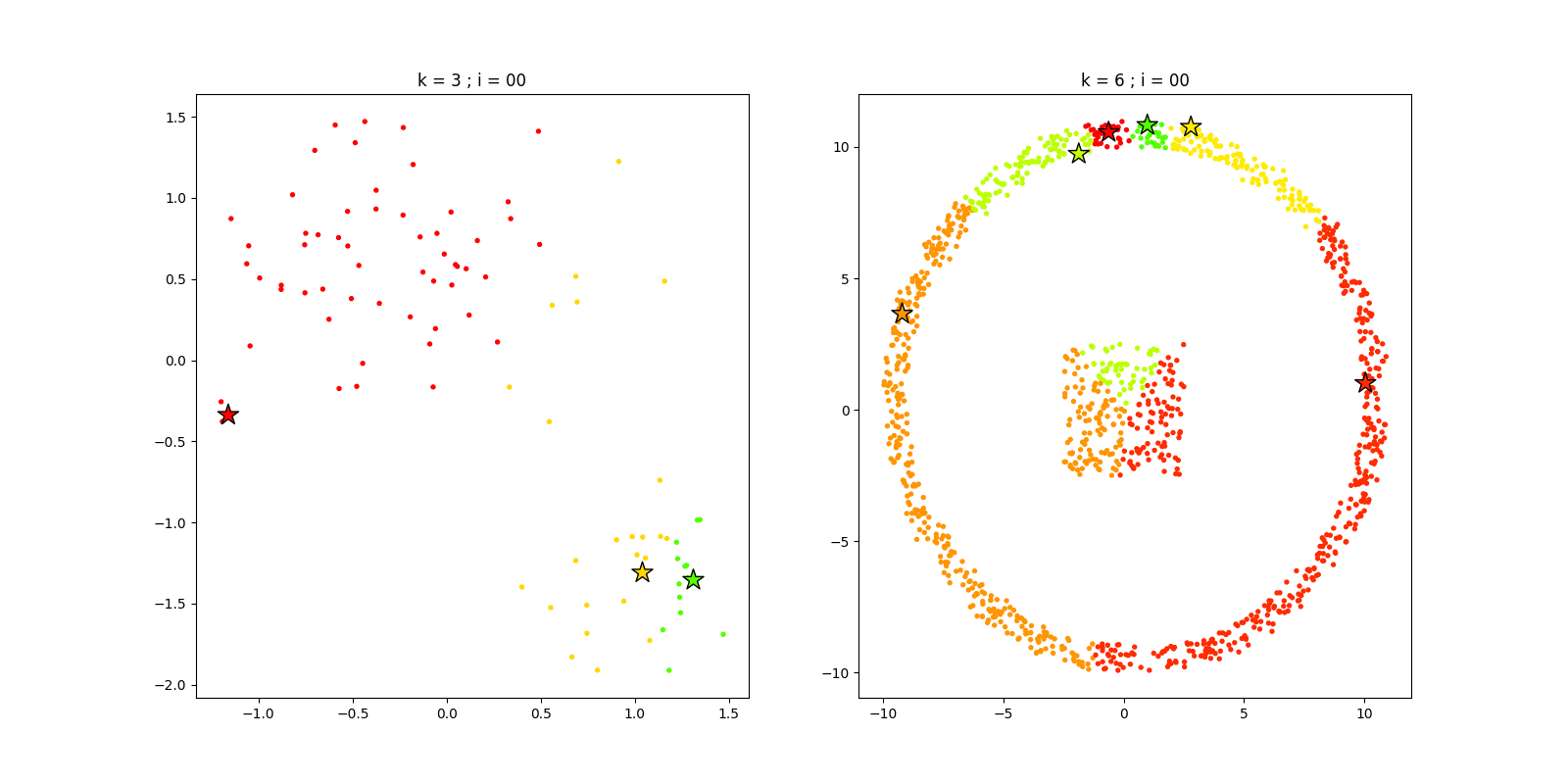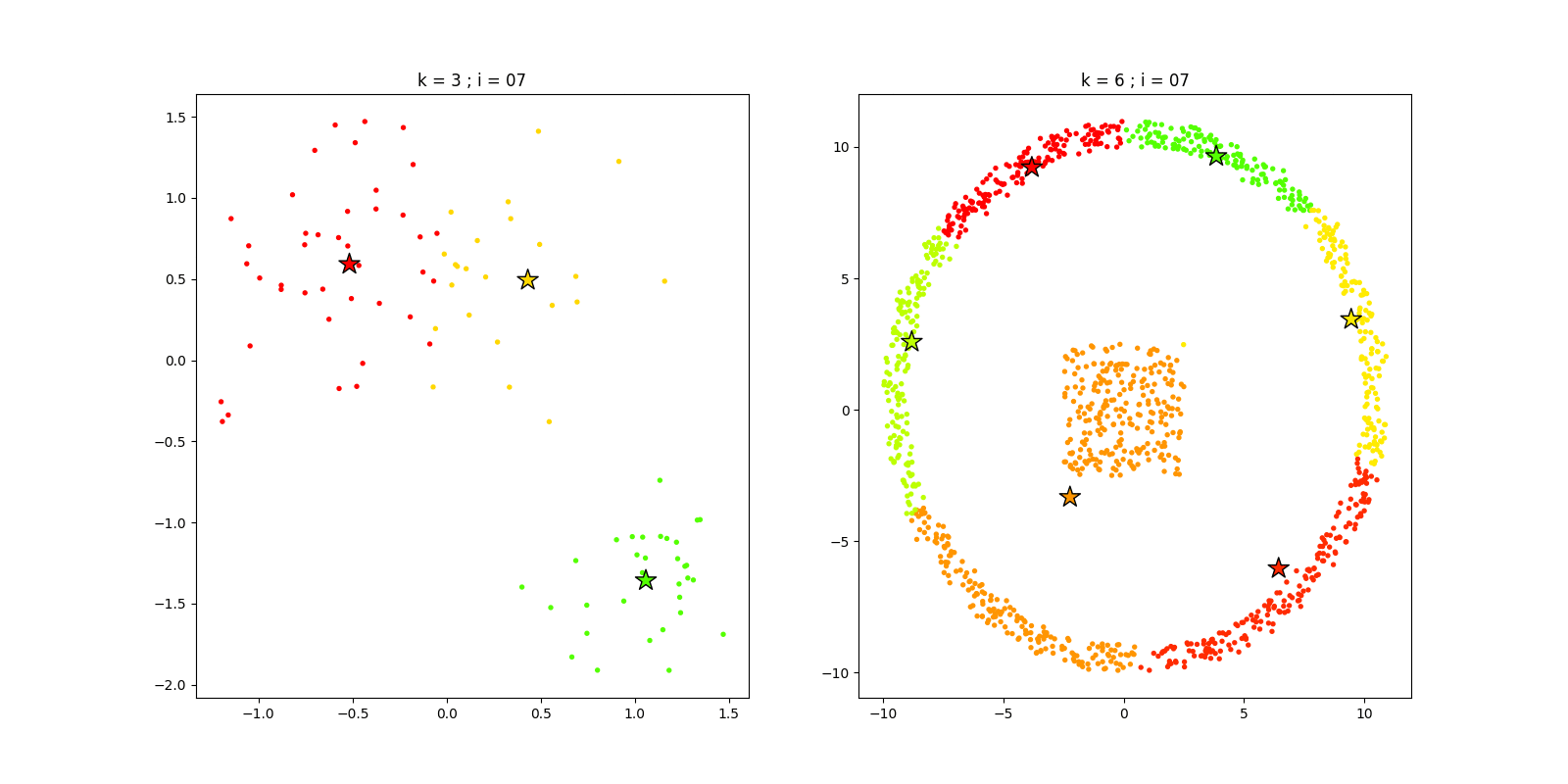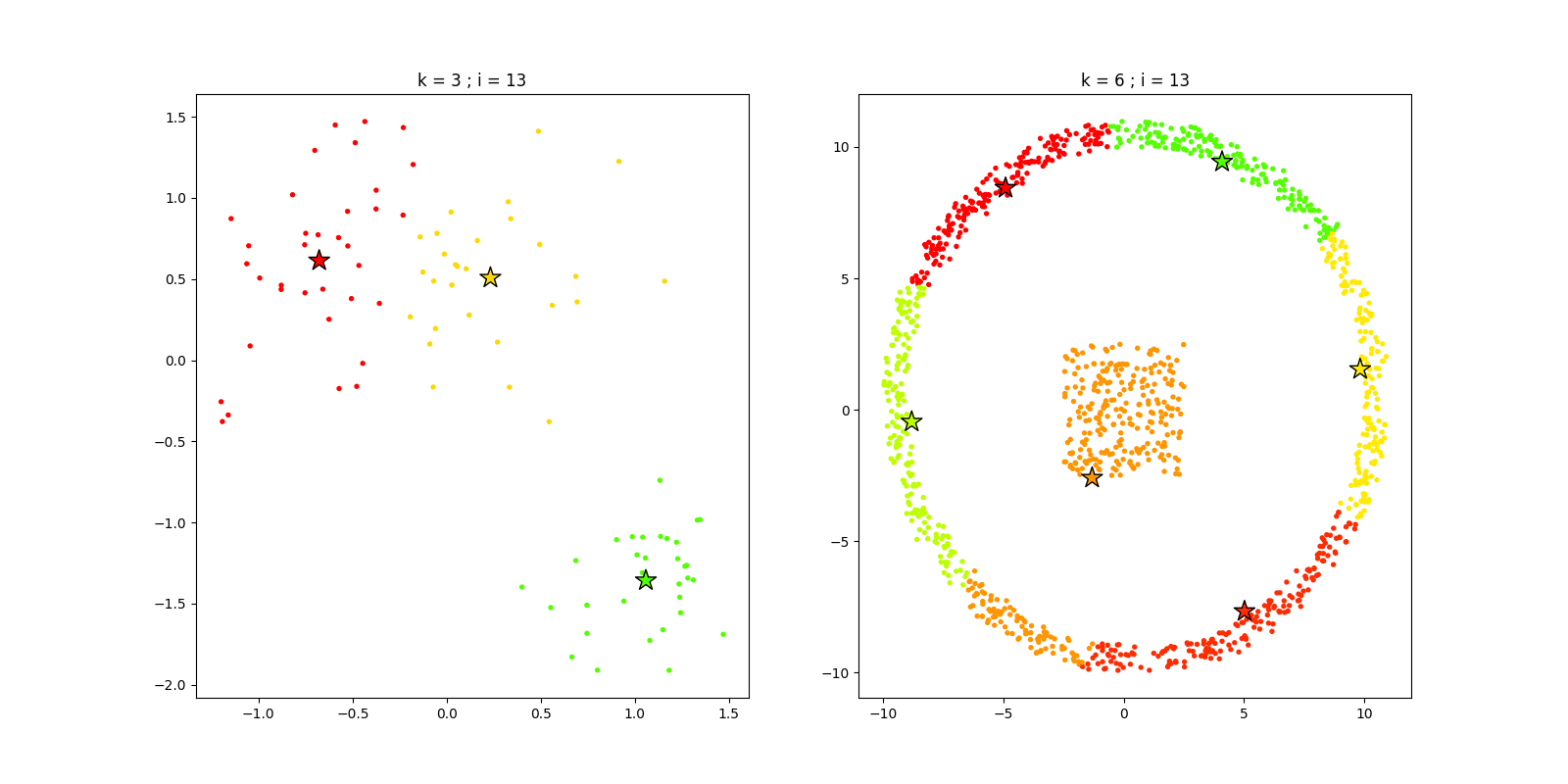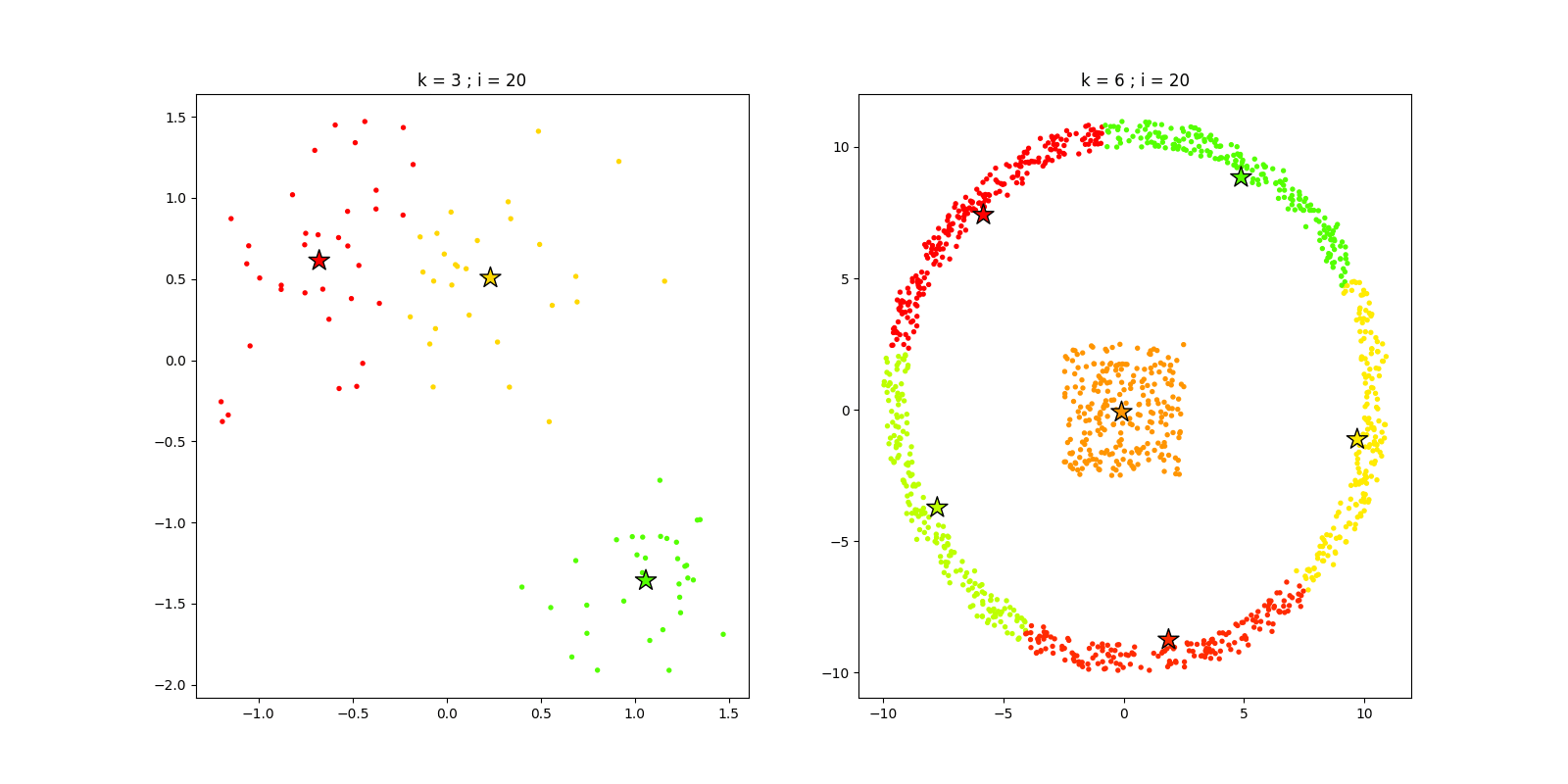
iters = 20; seed = 6
K1 = 3
kmeans1 = kMeans(K1, iters, seed)
fnc1, C1 = kmeans1.pred(X1)
K2 = 6
kmeans2 = kMeans(K2, iters, seed)
fnc2, C2 = kmeans2.pred(X2)

运行结果如下:

5 总结

本文介绍了机器学习领域中k-means进行聚类的原理以及相应的代码实现,并给出了完整的代码示例.

您学废了吗?

6 参考

参考
链接一
链接二

关注公众号《AI算法之道》，获取更多AI算法资讯。

注： 完整代码，关注公众号，后台回复 kMeans , 即可获取。