【控制工程1】弹簧系统运动控制方案及simulink仿真

一、题目描述

如图 ，物块和滑轮的质量分别为 m1 和 m2，两弹簧的弹性系数分别为 k1 和 k2，滑轮的半径为 r；物块位移和滑轮的角位移分别为x和θ。绳与圆盘无相对滑动，滑轮所在的圆平面平行于水平面（位移x非重力方向）。
问题 1：列写该系统的运动方程；
问题 2：现对滑块位移 x 进行运动控制，需获取滑轮角度和滑块位移等信息或数据，请自行设计运动控制系统方案。

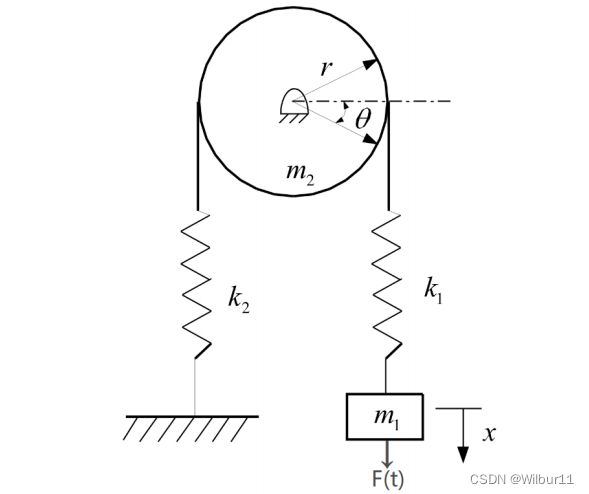
二、弹簧系统运动方程求解

解：设两弹簧弹力分别为${\mathrm{f}}_1$、${\mathrm{f}}_2$，对应的伸长量分别为${\mathrm{x}}_1$、${\mathrm{x}}_1$（拉伸正，压缩负)，物体初始位移为0 ，滑轮初始转动角度为 0（顺时针为正，逆时针为负）由牛顿第二定律 $\sum F_i=ma$ 和转动定律 $\sum M_i=J\alpha$ 可得下列方程：$$F_t-k_1{x}_1=m_1{a}_1=m_1\frac{d^{2}x}{d{t}^2}\text{\hspace{1em}(1)}$$$$k_1{x}_{1}r-k_2{x}_{2}r=\frac{m_2{r}^2}{2}{\alpha }_2=\frac{m_2{r}^2}{2}\frac{d^2\theta }{d{t}^2}\text{\hspace{1em}(2)}$$且有：$$x=x_1+x_2\text{\hspace{1em}(3)}$$$$x_2=r\theta \text{\hspace{1em}(4)}$$则由式(1)、(3)、(4)得：$$\theta =\frac{x-x_1}{r}=\frac{1}{r}\left(x-\frac{F_t}{k_1}+\frac{m_1}{k_1}\frac{d^{2}x}{d{t}^2}\right)\text{\hspace{1em}(5)}$$将式(1)、(4)、(5)带入式(2)，化简即可得弹簧系统的运动方程：$$\frac{m_2}{2k_1}\frac{d^2{F}_t}{d{t}^2}+\frac{k_1+k_2}{k_1}{F}_t=\frac{m_1{m}_2}{2k_1}\frac{d^{4}x}{d{t}^4}+\left(\frac{m_2{k}_1+2m_1{k}_1+2m_1{k}_2}{2k_1}\right)\frac{d^{2}x}{d{t}^2}+k_{2}x\text{\hspace{1em}(6)}$$

三、弹簧系统运动控制方案分析

3.1 弹簧系统传递函数

对式(6)进行拉氏变换：$$\left[\frac{m_2}{2k_1}{s}^2+\frac{k_1+k_2}{k_1}\right]F_t(s)=\left[\frac{m_1{m}_2}{2k_1}{s}^4+\left(\frac{m_2{k}_1+2m_1{k}_1+2m_1{k}_2}{2k_1}\right)s^2+k_2\right]X(s)\text{\hspace{1em}(7)}$$即可得弹簧系统位置与控制力的传递函数：$$G(s)=\frac{X(s)}{F_t(s)}=\frac{m_2{s}^2+2k_1+2k_2}{m_1{m}_2{s}^4+\left(m_2{k}_1+2m_1{k}_1+2m_1{k}_2\right)s^2+2k_1{k}_2}\text{\hspace{1em}(8)}$$

3.2 弹簧系统稳定性分析

首先定义弹簧系统的物理参数，以便后续simulink仿真与系统分析：

那么， 弹簧系统的传递函数可以写出来：

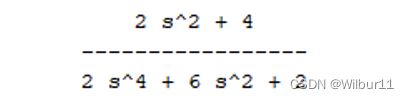
用matlab的函数判断弹簧系统稳定性：

输出1，说明弹簧系统本身是稳定的（可以想象到静态无外力下，弹簧系统自身保持稳定，但也许吹弹可破…）。

3.3 弹簧系统运动控制闭环框图

问题2要求对物块位置进行控制，也就是位置控制。一般闭环控制系统包括控制器、执行器、被控对象三部分组成，此问题弹簧系统就是我们的被控对象，那么系统运动控制闭环框图如下：

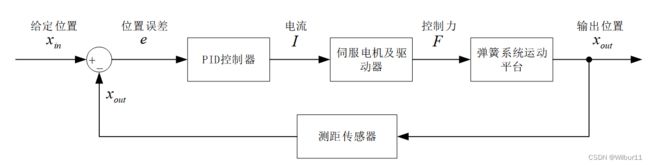
3.4 伺服电机选型

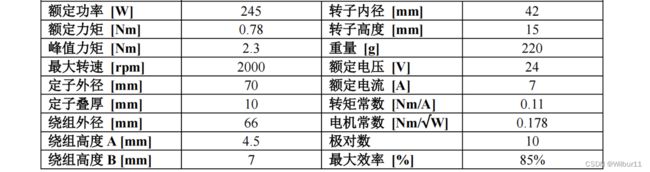
为了将控制力加在物块上，我们需要选择一个能够输出力的控制装置，这里我选择直流力矩电机（百度图片搜索的，侵权请联系删除）：

它的输出力与输入电流成正比，即正常工作时转矩=转矩常数×电流$$M={\mathrm{K}}_t\cdot I\text{\hspace{1em}(9)}$$重要参数如下（与上图无关）：

四、simulink仿真

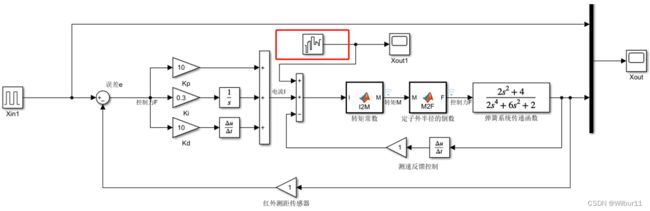
4.1 基于PID控制的simulink连线框图

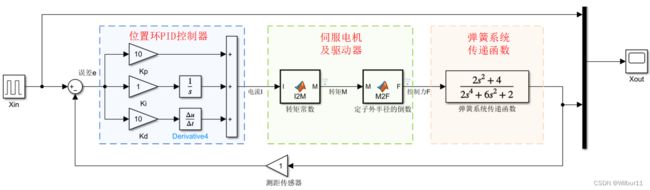
其中，I2M.m函数将PID控制器输出的电流 I 转化为电机的转矩 M，且根据峰值转矩限制了电流的大小：

M2F.m函数将电机转矩 M 转化为输出力 F：

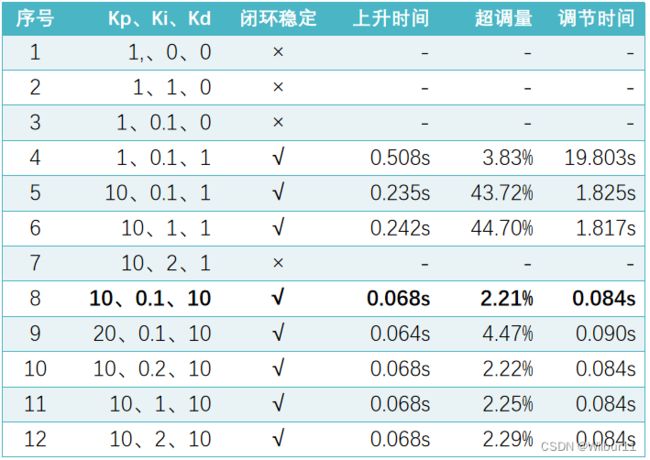
4.2 PID调参结果及位置跟踪曲线

调整PID参数，测试闭环系统的阶跃响应，此部分在matlab下写代码完成：

在simulink中，测试效果如下：

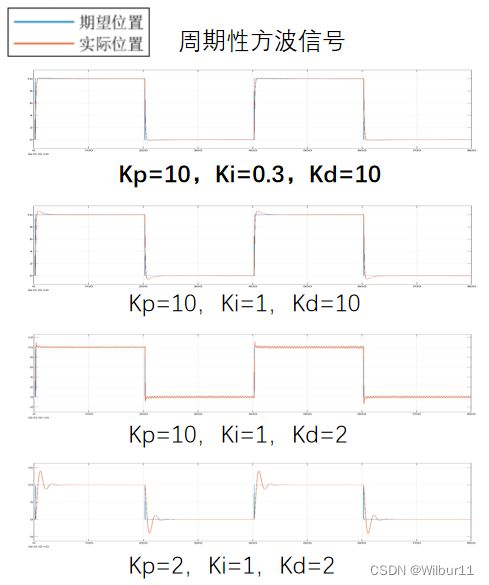
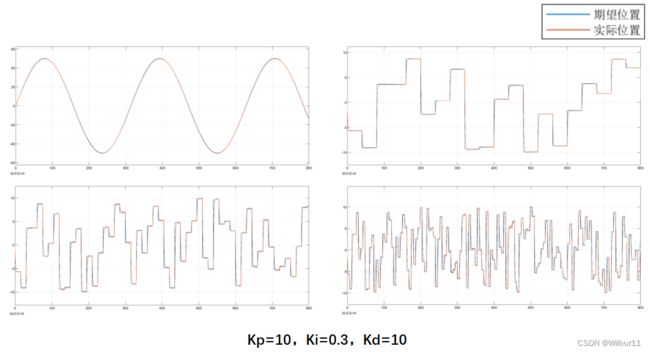
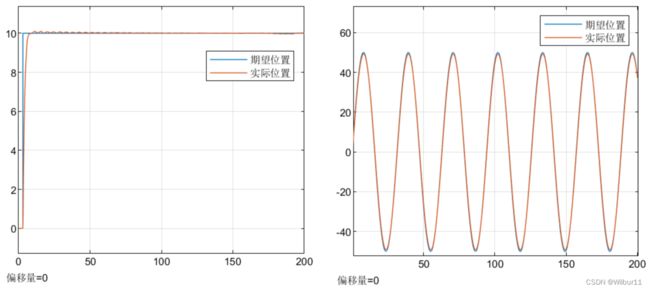
可以看出，通过合理的设置PID参数，闭环系统能够较好的跟踪输入的位置信号。

4.3 加入测速反馈控制的simulink框图

测速反馈控制将输出量的速度信号采用负反馈的形式反馈到输入端并与误差信号比较，构成的回路称为速度反馈控制（velocity feedback control）。如果输出量是机械位移，可采用测速装置将机械量转换成正比于输出速度的电信号，从而获得速度反馈，即通过引入速度反馈来改善系统性能。它具有的如下特点

• 可以有效地抑制作用在内回路各元件上的各种扰动，减小元件参数变化和非线性特性对系统性能的影响
• 可以分别调整前向通道和反馈通道的参数，以期单独改变系统某一方面的性能
• 由于反馈校正信号是从高功率点向低功率点传递，通常可不必另加放大器

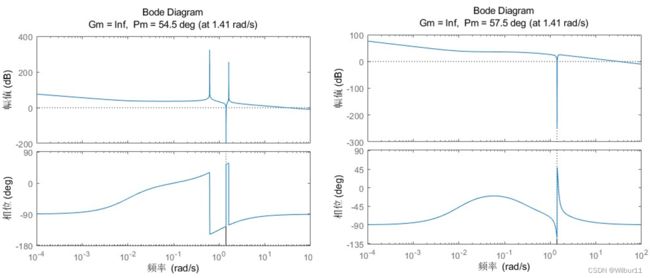
我们可以对比加入测速反馈控制前后系统Bode图，加入测速反馈控制后，相角裕度有所提升，动态性能更好：

4.4 PID控制结果对比

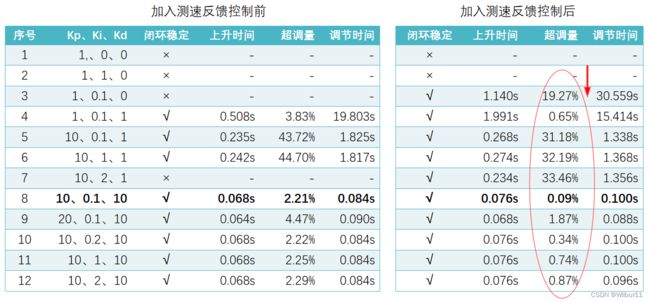
可以看出，加入测速反馈控制后，系统阶跃响应的超调量有明显下降。

4.5 测试系统在噪声下的响应

我们可以在simulink中加入Band-Limited White Noise，它是模块服从正态分布N(μ,σ)的随机数，它的能量可以视为σ2（即它的方差）：

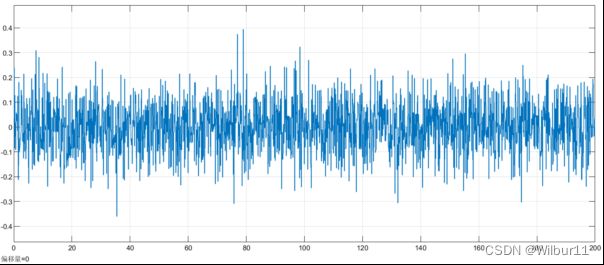
噪声在示波器的显示：

加入噪声以后的闭环系统框图 ：

系统在噪声干扰下的跟踪效果（有可能会跟踪失效，需要调整PID参数）：

总结

1. 建模并求解弹簧系统的运动方程及传递函数
2. 分析并设计弹簧系统闭环运动控制方案
3. 运用matlab和simulink对闭环系统建模和仿真，调优PID参数以提高系统性能，并对比了位置环控制和位置环＋测速反馈控制方案的效果，且验证了系统在有噪声环境下也能实现位置跟踪。

至此完成了弹簧系统运动控制方案的设计及simulink仿真，希望能对读者有一点点帮助。由于笔者学识尚浅，文中不正当之处欢迎指出！