K-means
6.1 聚类算法简介
学习目标
- 知道聚类算法的概念
- 了解聚类算法和分类算法的最大区别
1 认识聚类算法
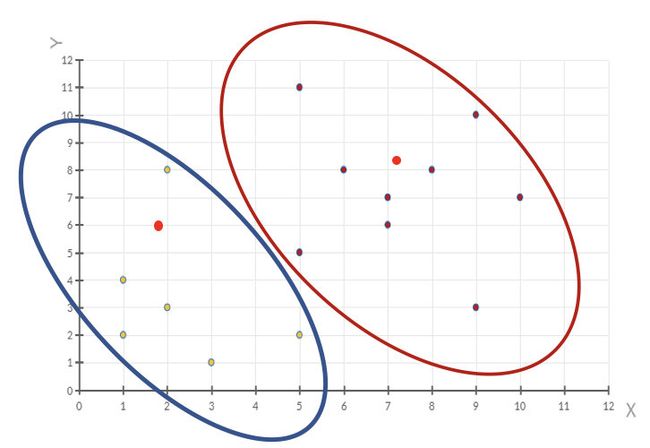
使用不同的聚类准则,产生的聚类结果不同。
1.1 聚类算法在现实中的应用
- 用户画像,广告推荐,Data Segmentation,搜索引擎的流量推荐,恶意流量识别
- 基于位置信息的商业推送,新闻聚类,筛选排序
- 图像分割,降维,识别;离群点检测;信用卡异常消费;发掘相同功能的基因片段
1.2 聚类算法的概念
聚类算法:
一种典型的无监督学习算法,主要用于将相似的样本自动归到一个类别中。
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算方法,会得到不同的聚类结果,常用的相似度计算方法有欧式距离法。
1.3 聚类算法与分类算法最大的区别
聚类算法是无监督的学习算法,而分类算法属于监督的学习算法。
6.2 聚类算法实现流程
学习目标
- 掌握K-means聚类的实现步骤
- k-means其实包含两层内容:
- K : 初始中心点个数(计划聚类数)
- means:求中心点到其他数据点距离的平均值
1 k-means聚类步骤
- 1、随机设置K个点作为初始的聚类中心
- 2、对于其他每个点计算到K个中心的距离,其它的点距离哪个中心点近,就归为哪一类。
- 3、对于属于同一个类的数据,计算平均值作为新的聚类中心点。
- 4、如果计算得出的新中心点与上一次的中心点一样(质心不再移动),那么结束,否则重新进行第二步过程
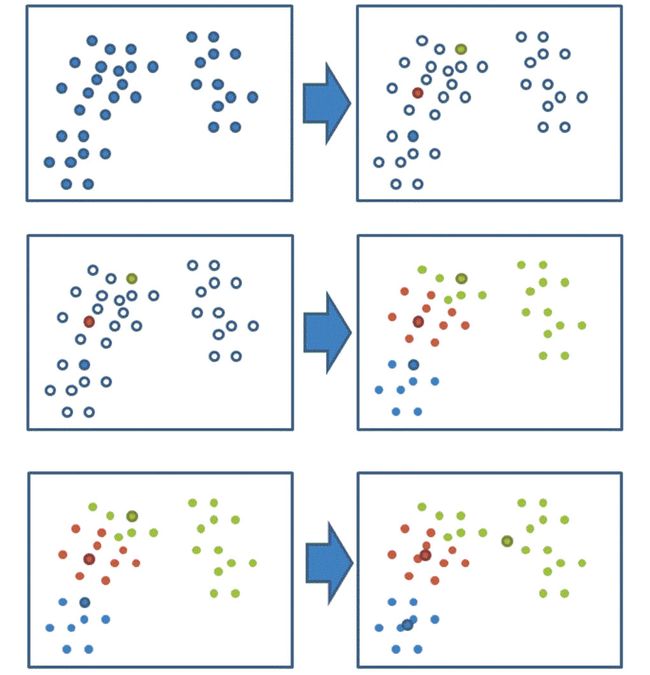
通过下图解释实现流程:
2 案例练习
- 案例:
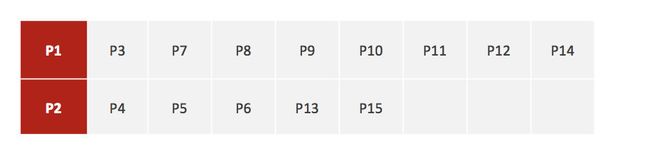
- 1、随机设置K个特征空间内的点作为初始的聚类中心(本案例中设置p1和p2)
2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
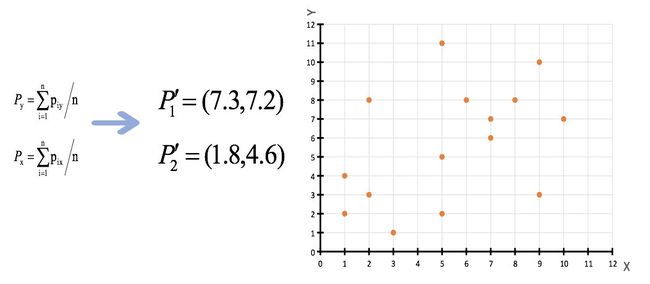
3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
4、如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程【经过判断,需要重复上述步骤,开始新一轮迭代】
5、当每次迭代结果不变时,认为算法收敛,聚类完成,K-Means一定会停下,不可能陷入一直选质心的过程。
3 小结
-
K-means聚类实现流程
【掌握】
-
事先确定常数K,常数K意味着最终的聚类类别数;
-
随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,
-
接着,重新计算每个类的质心(即为类中心),重复这样的过程,直到质心不再改变,
-
最终就确定了每个样本所属的类别以及每个类的质心。
-
注意
:
- 由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
-
6.3模型评估
学习目标
- 知道模型评估中的SSE、“肘”部法、SC系数和CH系数的实现原理
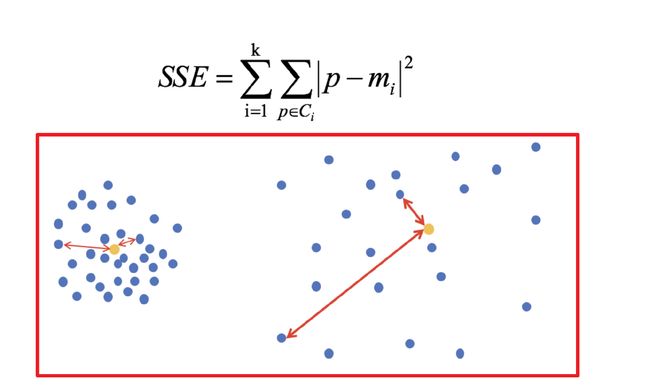
1 误差平方和(SSE,残差平方和):
举例:(下图中数据-0.2, 0.4, -0.8, 1.3, -0.7, 均为真实值和预测值的差)
在k-means中的应用:
公式各部分内容:
上图中: k=2
-
SSE随着聚类迭代,其值会越来越小,直到最后趋于稳定:
-
如果质心的初始值选择不好,SSE只会达到一个不怎么好的局部最优解.
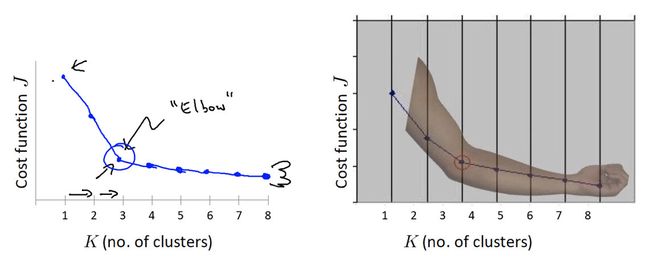
2 “肘”方法 (Elbow method) — K值确定
(1)对于n个点的数据集,迭代计算k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和;
(2)平方和是会逐渐变小的,直到k==n时平方和为0,因为每个点都是它所在的簇中心本身。
(3)在这个平方和变化过程中,会出现一个拐点也即“肘”点,下降率突然变缓时即认为是最佳的k值。
6.4 聚类算法api初步使用
学习目标
- 知道聚类算法API的使用
1 api介绍
- sklearn.cluster.KMeans(n_clusters=8)
- 参数:
- n_clusters:开始的聚类中心数量
- 整型,缺省值=8,生成的聚类数,即产生的质心(centroids)数。
- n_clusters:开始的聚类中心数量
- 方法:
- estimator.fit(x)
- estimator.fit_predict(x)
- 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)
- estimator.label_:模型的预测值
- estimator.inertia_:sse的值
- 参数:
2 案例
随机创建不同二维数据集作为训练集,并结合k-means算法将其聚类,你可以尝试分别聚类不同数量的簇,并观察聚类效果:(聚类参数n_cluster传值不同,得到的聚类结果不同)
2.1 代码实现
1.创建数据集
import matplotlib.pyplot as plt
#from sklearn.datasets.samples_generator import make_blobs
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
#KMeans:k-mean算法
#calinski_harabaz_score:值越大,聚类效果越好
#make_blobs: 创建用于聚类的数据集
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本2个特征,共4个簇,
# 簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
# 数据集可视化
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
2.使用k-means进行聚类,并使用sse方法评估
model = KMeans(n_clusters=3, random_state=9).fit(X)
# 分别尝试n_cluses=2\3\4,然后查看聚类效果
plt.scatter(X[:, 0], X[:, 1], c=model.labels_)
plt.show()
# 用sse评估的聚类分数
print(model.inertia_)
3 小结
- api:sklearn.cluster.KMeans(n_clusters=8)【知道】
- 参数:
- n_clusters:开始的聚类中心数量
- 方法:
- estimator.fit_predict(x)
- 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)
- estimator.fit_predict(x)
- 参数:
6.5 案例:探究用户对物品类别的喜好
学习目标
- 应用pca和K-means实现instacart公司的用户对物品类别的喜好细分划分
- 连接:https://www.kaggle.com/competitions/instacart-market-basket-analysis/data
数据如下:
- order_products__prior.csv:订单与商品信息
- 字段:order_id, product_id, add_to_cart_order, reordered
- products.csv:商品信息
- 字段:product_id, product_name, aisle_id, department_id
- orders.csv:用户的订单信息
- 字段:order_id,user_id,eval_set,order_number,….
- aisles.csv:商品所属具体物品类别
- 字段: aisle_id, aisle
1 需求
预测出用户下次想购买什么商品?
2 分析
- 1.获取数据
- 2.数据基本处理
- 2.1 合并表格
- 2.2 交叉表合并
- 2.3 数据截取
- 3.特征工程 — pca
- 4.机器学习(k-means)
- 5.模型评估(确定k值)
3 完整代码
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
- 1.获取数据
order_product = pd.read_csv("./data/instacart/order_products__prior.csv")
products = pd.read_csv("./data/instacart/products.csv")
orders = pd.read_csv("./data/instacart/orders.csv")
aisles = pd.read_csv("./data/instacart/aisles.csv")
-
2.数据基本处理
- 2.1 合并表格
# 2.1 合并表格 table1 = pd.merge(order_product, products, on="product_id")#使用内连接,连接两张表,只返回两个表中联结字段相等的数据 table2 = pd.merge(table1, orders, on="order_id") table = pd.merge(table2, aisles, on="aisle_id")- 2.2 交叉表合并
table = pd.crosstab(table["user_id"], table["aisle"]) #crosstab:交叉表,第一个是列明,第二个是行名,表示计算一列数据对于另外一列数据的分组个数(统计个数) #该交叉表表示用户购买的134种类别的个数。- 2.3 数据截取
data = table[:5000]#这个是因为电脑内存小,不是技巧 -
3.特征工程 — pca
transfer = PCA(n_components=0.96)#n_components=0.9保留96%的数据信息,是特征向量对应的特征值所占的比例
data = transfer.fit_transform(data)
- 4.机器学习(k-means)
labels = {}
sse = {}
for k in range(2, 10):
kmeans = KMeans(n_clusters=k, random_state=22).fit(data)
label = kmeans.labels_
labels[k] = label
sse[k] = kmeans.inertia_
- 5.k值可视化
plt.figure()
plt.plot(list(sse.keys()), list(sse.values()))
plt.xlabel("Number of cluster")
plt.ylabel("SSE")
plt.show()
6.确定k值等于3
kmeans = KMeans(n_clusters=3, random_state=22).fit(data)
label = kmeans.labels_
print(label)
kmeans.labels_
labels[k] = label
sse[k] = kmeans.inertia_
- 5.k值可视化
```python
plt.figure()
plt.plot(list(sse.keys()), list(sse.values()))
plt.xlabel("Number of cluster")
plt.ylabel("SSE")
plt.show()
6.确定k值等于3
kmeans = KMeans(n_clusters=3, random_state=22).fit(data)
label = kmeans.labels_
print(label)