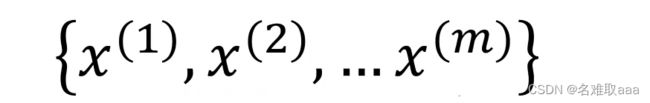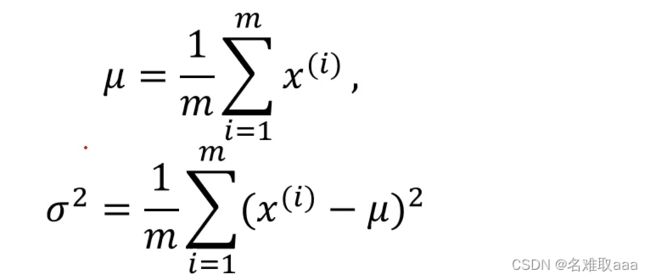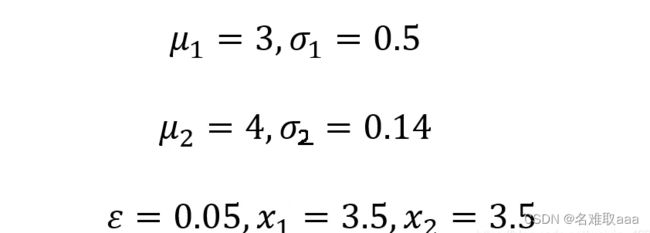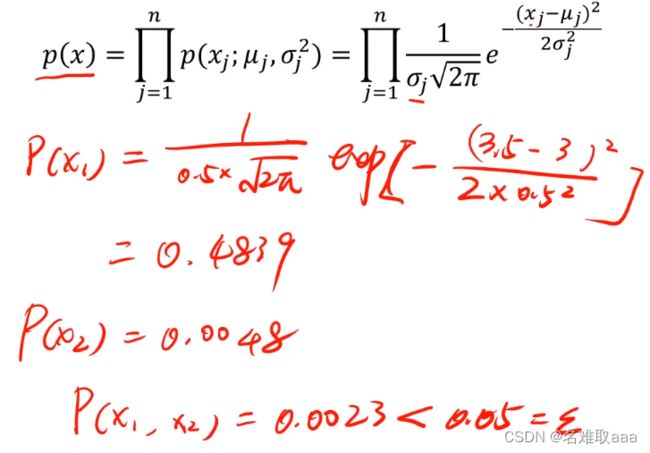机器学习之异常检测
文章目录
- 前言
- 異常檢測是什麽?
-
- 三大類異常檢測方法
- 热门方法
- 應用
- 異常點有哪幾種類型?
-
- 在异常检测中经常遇到哪些困难?
- 异常检测算法的分类
-
- 时序相关 VS 时序独立
- 全局检测 VS 局部检测
- 输出形式:标签 VS 异常分数
- 根据不同的模型特征
- 异常检测经典模型思想
-
- 统计检验方法
- 基于深度的方法
- 基于偏差的方法
- 基于密度的方法
- 深度学习方法
- 统计检验方法的過程
- 實戰
- 總結
前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容之異常檢測
異常檢測是什麽?
在数据挖掘中,异常检测(英语:anomaly detection)对不匹配预期模式或数据集中其他项目的项目、事件或观测值的识别。 通常异常项目会转变成银行欺诈、结构缺陷、医疗问题、文本错误等类型的问题。异常也被称为离群值、新奇、噪声、偏差和例外。
三大類異常檢測方法
- 在假设数据集中大多数实例都是正常的前提下,无监督异常检测方法能通过寻找与其他数据最不匹配的实例来检测出未标记测试数据的异常。
- 监督式异常检测方法需要一个已经被标记“正常”与“异常”的数据集,并涉及到训练分类器(与许多其他的统计分类问题的关键区别是异常检测的内在不均衡性)。
- 半监督式异常检测方法根据一个给定的正常训练数据集创建一个表示正常行为的模型,然后检测由学习模型生成的测试实例的可能性。
热门方法
- 基于密度的方法(最近邻居法、局部异常因子及此概念的更多变化)。
- 基于子空间与相关性的高维数据的孤立点检测。
- 一类支持向量机。
- 复制神经网络。
- 基于聚类分析的孤立点检测。
- 与关联规则和频繁项集的偏差。
- 基于模糊逻辑的孤立点检测。
- 运用特征袋、分数归一化与不同多样性来源的集成方法。
不同方法的性能在很大程度上取决于数据集和参数,比较许多数据集和参数时,各种方法与其他方法相比的系统优势不大。
應用
异常检测技术用于各种领域,如入侵检测、欺诈检测、故障检测、系统健康监测、传感器网络事件检测和生态系统干扰检测等。它通常用于在预处理中删除从数据集的异常数据。在监督式学习中,去除异常数据的数据集往往会在统计上显著提升准确性
在工业上的应用:
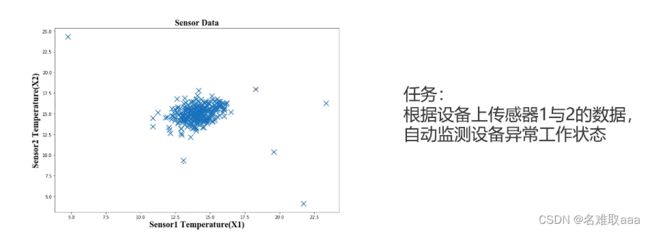
当检测设备是否处于异常工作状态时,可以由上图分析得到:那些零散的点对应的数据是异常数据。因为设备大多数时候都是处于正常工作状态的,所以数据点应该比较密集地集中在一个范围内,而那些明显偏出正常范围内的数据点就是我们要找的异常数据了,此时就可以自动监测到设备处于异常工作状态,就可以即使检查维修设备以避免不必要的损失。
在图像里的应用:

通过异常检测,我们也可以检测到图像中的异常图像。(如上图中的小红鱼)
此外,异常检测的应用还有很多,比如:
金融领域:从金融数据中识别”欺诈案例“,如识别信用卡申请欺诈、虚假信贷等;
网络安全:从流量数据中找出”入侵者“,并识别新的网络入侵模式;
电商领域:从交易数据中识别”恶意买家“,如羊毛党、恶意刷屏团伙;
生态灾难预警:基于对风速、降雨量、气温等指标的预测,判断未来可能出现的极端天气;
工业界:可通过异常检测手段进行工业产品的瑕疵检测,代替人眼进行测量和判断。
以下為整理網上資料做的筆記
異常點有哪幾種類型?
目前比较公认的分类方式是分为三种:
- 单点异常(Global Outliers):也可以称为全局异常,即某个点与全局大多数点都不一样,那么这个点构成了单点异常。例如,和三只小黄人相比,海绵宝宝的混入就可以算作是单点异常。
-
上下文异常(Contextual Outliers):这类异常多为时间序列数据中的异常,即某个时间点的表现与前后时间段内存在较大的差异,那么该异常为一个上下文异常点。例如,在某个温带城市夏天的气温时序数据中,其中有一天温度为10℃,而前后的气温都在25-35℃的范围,那么这一天的气温就可以说是一个上下文异常。
-
集体异常(Collective Outliers):这类异常是由多个对象组合构成的,即单独看某个个体可能并不存在异常,但这些个体同时出现,则构成了一种异常。集体异常可能存在多种组成方式,可能是由若干个单点组成的,也可能由几个序列组成。想象这样一个场景,某小区某天有一户人家搬家了,这是一件很正常的事,但如果同一天有10户同时搬家了,那就构成了集体异常,显然这不是一个正常小区会时常发生的事情。
在异常检测中经常遇到哪些困难?
- 在大多数实际的场景中,数据本身是没有标签的,也存在一些数据集有标签,但标签的可信度非常低,导致放入模型后效果很差,这就导致我们无法直接使用一些成熟的有监督学习方法。
- 常常存在噪音和异常点混杂在一起的情况,难以区分。
- 在一些欺诈检测的场景中,多种诈骗数据都混在一起,很难区分不同类型的诈骗,因为我们也不了解每种诈骗的具体定义。
由于没有准确的标签,也没有对具体诈骗类型的理解,就导致我们陷入鸡生蛋 or 蛋生鸡的循环之中。要解决这种情况,目前比较常用的手段是,将无监督学习方法和专家经验相结合,基于无监督学习得到检测结果,并让领域专家基于检测结果给出反馈,以便于我们及时调整模型,反复进行迭代,最终得到一个越来越准确的模型
异常检测算法的分类
异常检测涉及的场景非常丰富,那么异常检测算法可以从哪些角度进行分类呢?一般可以从以下四个角度作区分:
- 时序相关 VS 时序独立
- 全局检测 VS 局部检测
- 输出形式:标签 VS 异常分数
- 根据不同的模型特征
时序相关 VS 时序独立
首先可以根据该场景的异常是否与时间维度相关。在时序相关问题中,我们假设异常的发生与时间的变化相关,比如一个人平时的信用卡消费约为每月5000元,但11月的消费达到了10000元,那这种异常的出现就明显与时间维度相关,可能是因为”万恶“的双十一。
而在时序独立问题中,我们假设时间的变化对异常是否发生是无影响的,在后续的分析建模中,也就不会代入时间维度。
全局检测 VS 局部检测
在全局检测方法中,针对每个点进行检测时,是以其余全部点作为参考对象的,其基本假设是正常点的分布很集中,而异常点分布在离集中区域较远的地方。这类方法的缺点是,在针对每个点进行检测时,其他的异常点也在参考集内,这可能会导致结果可能存在一定偏差。
而局部检测方法仅以部分点组成的子集作为参考对象,基于的假设是,正常点中可能存在多种不同的模式,与这些模式均不同的少数点为异常点。该类方法在使用过程中的缺点是,参考子集的选取比较困难。
输出形式:标签 VS 异常分数
这种分类方式是根据模型的输出形式,即直接输出标签还是异常分数。输出标签的方法比较简单直观,可以直接根据模型输出的结果判断每个点是否为异常点。
使用可以输出异常得分的模型,我们可以进一步看哪些点的异常程度更高,也可以根据需要设定阈值,比如设定百分比,找出异常程度排在前10%的异常点。
根据不同的模型特征
还可以根据模型本身的特点进行分类,大致可以分为以下几种:
- 统计检验方法
- 基于深度的方法
- 基于偏差的方法
- 基于距离的方法
- 基于密度的方法
- 深度学习方法
异常检测经典模型思想
统计检验方法
使用这类方法基于的基本假设是,正常的数据是遵循特定分布形式的,并且占了很大比例,而异常点的位置和正常点相比存在比较大的偏移。
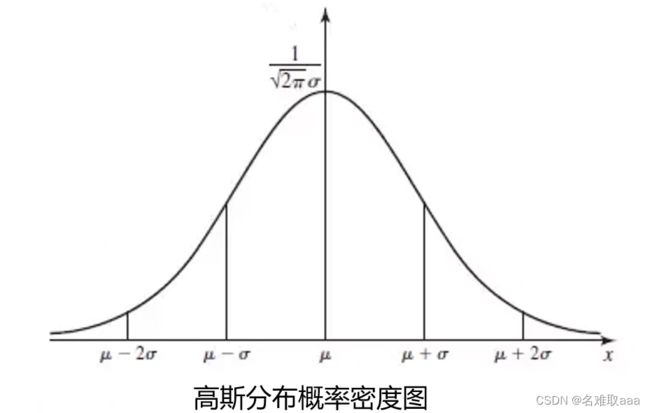
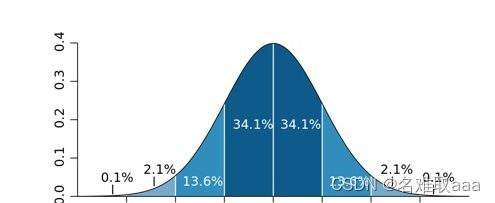
比如高斯分布,在平均值加减3倍标准差以外的部分仅占了0.2%左右的比例,一般我们把这部分数据就标记为异常数据。
使用这种方法存在的问题是,均值和方差本身都对异常值很敏感,因此如果数据本身不具备正态性,就不适合使用这种检测方法。
基于深度的方法
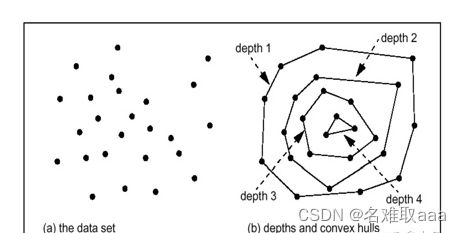
基于深度的方法,即从点空间的边缘定位异常点,按照不同程度的需求,决定层数及异常点的个数。如下图所示,圆中密密麻麻的黑点代表一个个数据点,基于的假设是点空间中心这些分布比较集中、密度较高的点都是正常点,而异常点都位于外层,即分布比较稀疏的地方。

如下图,最外层点的深度为1,再往内几层深度一次为2、3、4…… 若我们设置阈值k=2,那么深度小于等于2的点就全部为异常点。这一方法最早由 Tukey 在1997年首次提出。
但这个基础模型仅适用于二维、三维空间。现在有很多流行的算法都借鉴了这种模型的思想,但通过改变计算深度的方式,已经可以实现高维空间的异常检测,如孤立森林算法
基于偏差的方法
这是一种比较简单的统计方法,最初是为单维异常检测设计的。给定一个数据集后,对每个点进行检测,如果一个点自身的值与整个集合的指标存在过大的偏差,则该点为异常点。
具体的实现方法是,定义一个指标 SF(Smooth Factor),这个指标的含义就是当把某个点从集合剔除后方差所降低的差值,我们通过设定一个阈值,与这些偏差值进行比较来确定哪些点存在异常。这个方法是由 Arning 在1996年首次提出的。
之后基于最初这个模型,又出现了基于嵌套循环、基于网格的距离模型,再之后就是我们熟知的 kNN、KMeans,都可以通过计算距离来做异常检测。
基于密度的方法
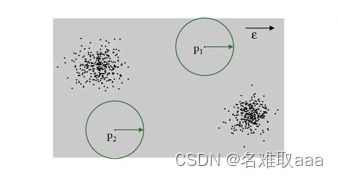
与基于距离的方法类似,该类方法是针对所研究的点,计算它的周围密度和其临近点的周围密度,基于这两个密度值计算出相对密度,作为异常分数。即相对密度越大,异常程度越高。基于的假设是,正常点与其近邻点的密度是相近的,而异常点的密度和周围的点存在较大差异。
设计这种方法的动机是,基于距离的异常检测方法不能很好地处理一些密度存在差异的数据集。如下图中的数据点分布,如果使用基于距离的模型,半径和比例已经设定好了,点 o2 很容易被识别为异常点,因为右上的 C1 子集中很多点与周围点的距离要比 o2 还小,其中很多点就会被标为正常点。但如果从密度的角度来看,o2 更像是一个正常点。所以无论单从哪个角度看,我们都可能会忽略另一个维度上的特征,因此还是要根据具体场景和目标任务,以及数据集本身的特点来进行算法的选择,或是进行算法的结合。
深度学习方法
目前最常用于异常检测的深度学习方法要非 Autoencoder 莫属了。
Autoencoder 的中文名叫自编码器,由 Encoder(编码器)和 Decoder(解码器)两部分构成,如下图:
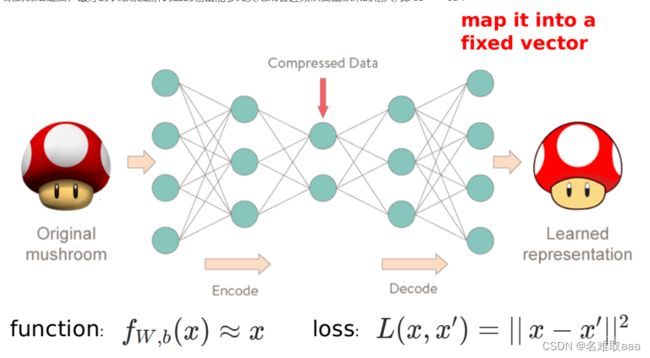
左边部分为编码器,它可以把高维的输入压缩成低维的形式来表示,在此过程中,神经网络会尽量留下有用的信息,去除掉一些不重要的信息和噪声。右边部分为解码器,它负责把压缩了的数据再进行还原,努力恢复成原本的样子。妥妥的自己训练自己,是一个自力更生的模型!
统计检验方法的過程
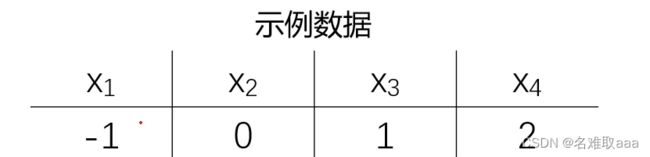
假设我们有一个一维的数据集,在这个数据集中有m个样本:
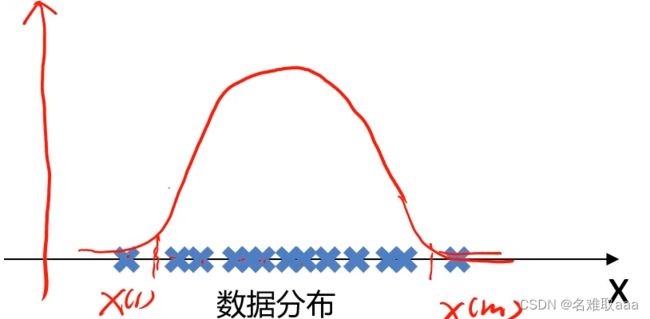
数据在x轴的分别如下图:
我们的目标是自动地找出这上面的异常样本,就可以根据样本在坐标轴上分布的数量多少,计算出坐标轴上各点对应的样本的概率密度,可以设定当概率密度小于某个值时,这时其对应的样本就是我们要找的异常样本。
概率密度:概率密度函数是一个描述随机变量在某个确定的取值点附近的可能性的函数
这里说一下高斯分布的概率密度函数:
了解了高斯分布概率密度函数后,怎样通过高斯分布概率密度函数去解决异常检测问题呢?这里仍以上述的一维数据为例。
在我们知道X1、X2……Xm这些数据后,就可以进行相应计算了。
- 计算数据均值u,标准差σ
- 计算对应的高斯分布概率密度函数
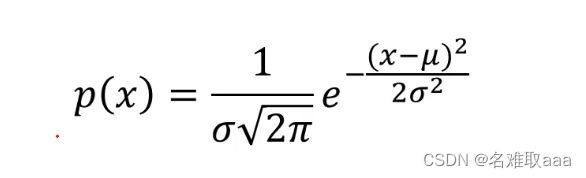
计算出来后,数据对应的高斯分布概率密度函数如下图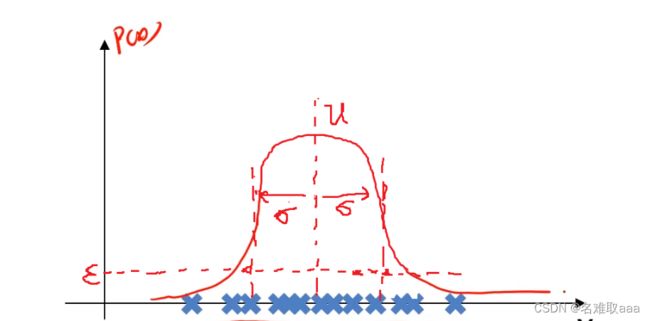
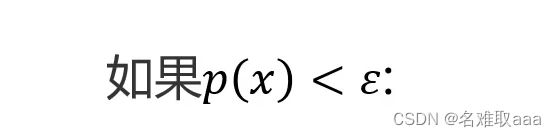
如果高于一维怎么办?
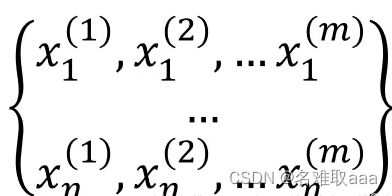
比如这里n维的数据,每一个维度都有m个样本。若要计算其高斯分布概率密度函数,可按如下步骤:
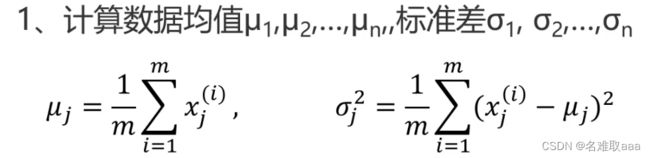
先计算出每一个维度下对应的均值和标准差了,这样就可以计算每个维度下的概率密度函数

我们将计算出的每个维度下的概率密度函数相乘就可以计算出总的概率密度函数了
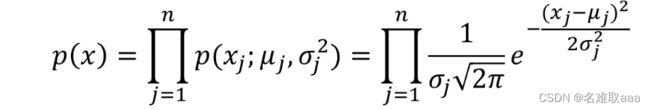
這個符號為累乘
最后再根据高维下的概率密度函数判断其是否小于预期就可以判断异常点了
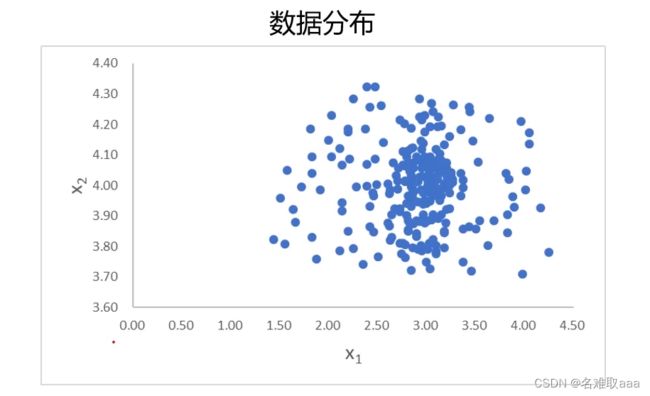
下面给出一组二维数据,来判断当x1=3.5,x2=3.5时,对应的点是不是异常点
经计算可判断该点为异常点
下图是二维数据下的一个概率密度函数图
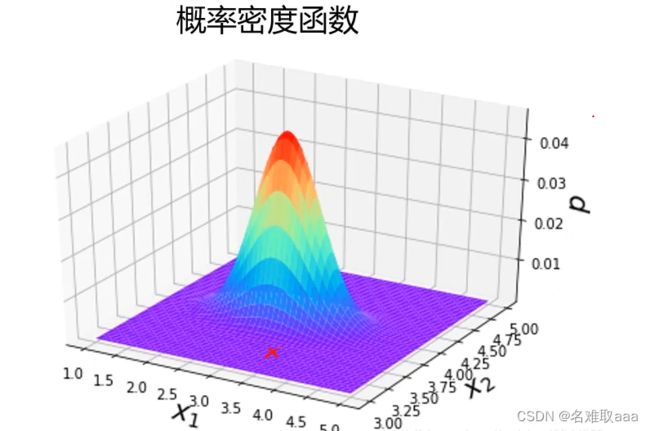
此时异常点在图中的位置大概是这样的
可以看出该点明显异常
實戰
異常檢測實戰task:
- 基於anomaly_data.csv數據,可視化數據分佈情況,及其對應高斯分佈的概率密度
- 建立模型,實現異常數據點預測
- 可視化異常檢測處理結果
- 修改概率分佈閾值EllipticEnvelope(contamination=0.1)中的contamination,查看閾值改變對結果的影響
#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('anomaly_data.csv')
data.head()
預覽看看數據加載正常嗎
#visualize the data
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(10,5))
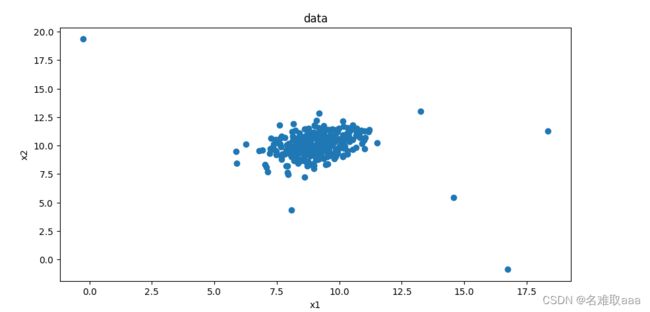
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'])
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
定義參數
#define x1 and x2
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']
fig2 = plt.figure(figsize=(20,5))
plt.subplot(121)
plt.hist(x1,bins=100)
plt.title('x1 distribution')
plt.xlabel('x1')
plt.ylabel('counts')
plt.subplot(122)
plt.hist(x2,bins=100)
plt.title('x2 distribution')
plt.xlabel('x2')
plt.ylabel('counts')
plt.show()
在一個畫布可視化看看
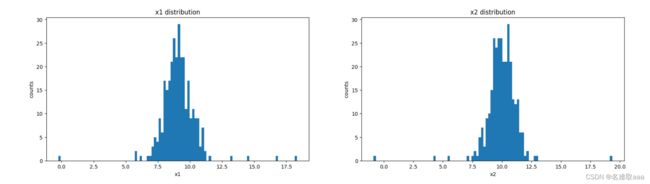
也可以修改 bins 的參數看看差別,大一點就細緻一點
#calculate the mean and sigma of x1 and x2
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean,x1_sigma,x2_mean,x2_sigma)
计算x1和x2的平均值和標準差
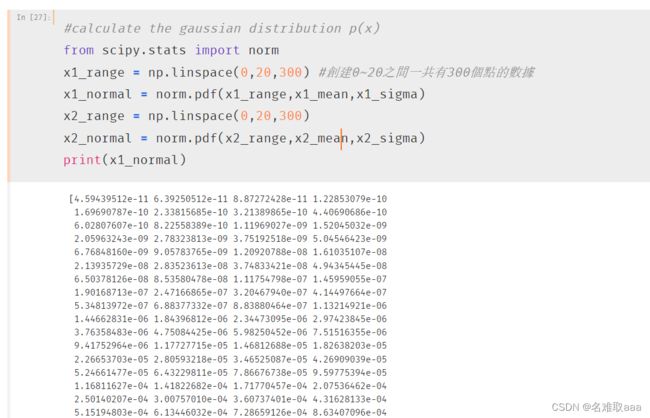
#calculate the gaussian distribution p(x)
from scipy.stats import norm
x1_range = np.linspace(0,20,300) #創建0~20之間一共有300個點的數據
x1_normal = norm.pdf(x1_range,x1_mean,x1_sigma)
x2_range = np.linspace(0,20,300)
x2_normal = norm.pdf(x2_range,x2_mean,x2_sigma)
print(x1_normal)
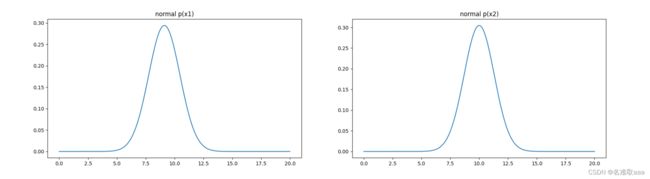
#visualize the p(x)
fig2 = plt.figure(figsize=(20,5))
plt.subplot(121)
plt.plot(x1_range,x1_normal)
plt.title('normal p(x1)')
plt.subplot(122)
plt.plot(x2_range,x2_normal)
plt.title('normal p(x2)')
plt.show()
可視化概率密度函數
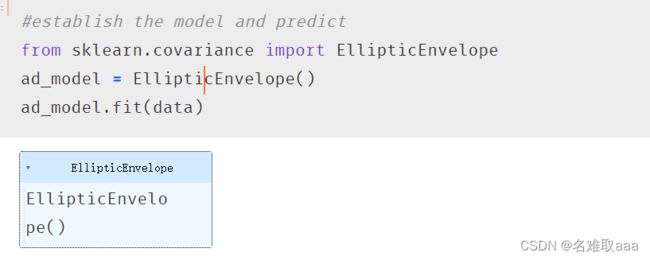
#establish the model and predict
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope()
ad_model.fit(data)
#make prediction
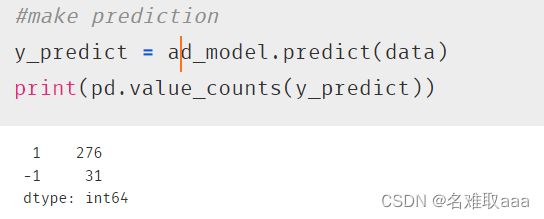
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
做出預測,看一下分佈大概是10%這樣,-1就是異常點的數據
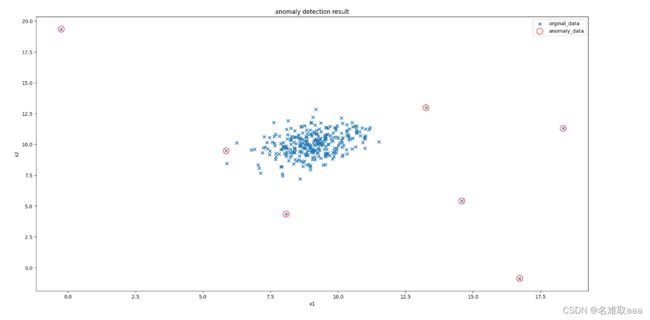
#visualize the result
fig4 = plt.figure(figsize=(20,10))
orginal_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x') #marker 修改標記樣子
anomaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1]
,marker='o',facecolor='none',edgecolors='red',s=150) #facecolor填充色,edgecolors顔色,s尺寸
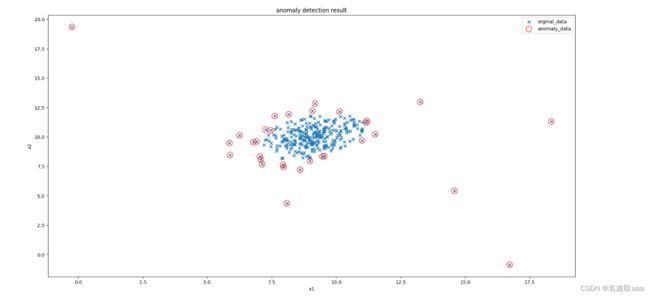
plt.title('anomaly detection result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((orginal_data,anomaly_data),('orginal_data','anomaly_data'))
plt.show()
可視化看一下,效果還可以的
ad_model = EllipticEnvelope(contamination=0.02)
ad_model.fit(data)
y_predict = ad_model.predict(data)
fig5 = plt.figure(figsize=(20,10))
orginal_data=plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],marker='x') #marker 修改標記樣子
anomaly_data=plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1]
,marker='o',facecolor='none',edgecolors='red',s=150) #facecolor填充色,edgecolors顔色,s尺寸
plt.title('anomaly detection result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((orginal_data,anomaly_data),('orginal_data','anomaly_data'))
plt.show()
將參數 contamination 修改為0.02,可以對比起上面看出在比較密集的地方就少了一些異常點少了誤判,更好了一點
總結
通過計算數據各維度對應的搞事分佈概率密度函數,可用於尋找到數據中的異常點
通過修改概率密度閾值contamination,可調整異常點檢測的靈敏度
這就是本次學習異常檢測的筆記
附上本次實戰的數據集和源碼:
鏈接:https://github.com/fbozhang/python/tree/master/jupyter