R-CNN 详解
文章目录
- 测试流程
-
- Selective Search
- Warp
- CNN
- SVM
- NMS
- Bounding-box Regression
- 训练过程
-
- 准备样本
- CNN Pre-training
- CNN Fine-tuning
- SVM Training
- Bounding-box Regression Training
- 缺点
- 参考文献
- 附录
2014 CVPR 录用了 Ross Girshick 的论文《Rich feature hierarchies for accurate object detection and semantic segmentation 》,文章提出了经典目标检测模型——区域卷积神经网路(R-CNN, Regions with CNN features)。R-CNN 是一种两阶段(two-stage)的目标检测模型,即先在图片上生成候选区域(region proposals),而后对候选区域进行识别。
测试流程
R-CNN 在图片上进行目标检测的测试流程大致如下:
- 使用选择性搜索算法(Selective Search, SS)算法在一张图片上生成众多候选区域。
- 将尺寸各异的候选区域缩放(warp)成固定大小的区域。
- 将扭曲后的候选区域送入 CNN 提取出特征向量。
- 依据特征向量,使用 SVM 对候选区域进行分类并打分。
- 结合各候选区域及其打分情况,使用非极大值抑制(Non-Maximum Suppression, NMS)算法挑选出最终的预测区域。
- 使用边框回归(Bounding-box regression, BBS)对预测区域进行修正。
Selective Search
SS 算法来自于 J. Uijlings 在 IJCV 2013 上的论文《Selective search for object recognition》。算法首先将图片划分成很多小区域,而后计算区域之间的相似度进行合并。不了解 SS 算法并不影响对 R-CNN 的理解,所以我们在此不进行详细讨论。
R-CNN 使用 SS 算法为每张图片生成 2000 2000 2000 个候选区域(region proposal)。
Warp
R-CNN 使用的 CNN 限制输入的图片必须是固定的尺寸 227 × 227 227\times227 227×227,由于候选区域的比例和大小各异,所以必须必须对其进行缩放操作。作者提出了两种缩放方法:
- 各项异性缩放:各向异性缩放就是不管候选区域比例如何,直接将其缩放为 227 × 227 227\times227 227×227,如下图中第 3 3 3 行 D D D 列所示。作者又尝试了先对候选区域进行填充(padding)而后再各向异性缩放。填充的内容是候选区域外部的像素,如 p a d d i n g = 16 padding=16 padding=16 即各向向外扩张 16 16 16 个像素。下图中第 4 4 4 行 D D D 列就是 p a d d i n g = 16 padding=16 padding=16 各向异性缩放的结果。
- 各项同性缩放:各向同性缩放就是保持原始比例进行的缩放。该方法又细分为了两种情况:
- 先扩充后裁剪:较窄的两侧向外扩充至整个区域变为正方形,而后进行缩放,如下图中第 3 3 3 行 B B B 列所示。该操作也可加入 padding,如下图中第 4 4 4 行 B B B 列所示。需要注意的是,如果扩充到图片的边界仍然没有变为正方形,那么将对空缺的区域进行填色,所填颜色的色度为整个区域的平均值,下图第 4 4 4 行 B B B 列的图片中左侧的灰条即为填色的结果。
- 先裁剪后扩充:按照候选区域进行裁剪,而后对空缺的地方进行填色,如下图中第 3 3 3 行 C C C 列所示。加入 padding 操作的结果如下图中第 4 4 4 行 C C C 列所示。
作者发现:各项异性缩放且 p a d d i n g = 16 padding=16 padding=16 的效果最好。
CNN
R-CNN 使用了 AlexNet8 作为 CNN。 AlexNet8 包含了 5 5 5 层卷积、 2 2 2 层全连接隐层和 1 1 1 层使用 softmax 的输出层,其中每层卷积后都有一个最大池化层。R-CNN 并未使用 AlexNet 的 softmax 输出层作为分类器,而是将其替代为多个 SVM 二分类器。换句话说,应用在 R-CNN 上的 CNN 只有 5 5 5 层卷积和 2 2 2 层全连接层。作者为什么不使用 softmax 层而使用 SVM 作分类器?这个问题,我们将在下文的训练过程中讨论。
网络的输入格式是 227 × 227 227\times227 227×227 RGB 图像,输出的是 4096 4096 4096 维的特征向量。
SVM
作者为每一类事物都训练了一个 SVM 二分类器。假如要检测 n n n 类事物,那么就需要 n + 1 n+1 n+1 个 SVM 二分类器,其中一个用于检测图片中的背景。每个 SVM 分类器都会输出一个概率,如果某类输出的概率值大于或等于阈值(常设为 0.5 0.5 0.5),那么该候选区域会被留在该类并记录其概率值;小于则被抛弃。
NMS
每个类别独立地运行 NMS 算法,进一步筛选被留在本类的候选区域。算法的运行过程大致如下:
- 找出所有候选区域的集合 D D D 中概率值最大的一个区域 a a a 并为其打上标记。
- 找出 D D D 中未被标记的区域 b b b。
- 令 b b b 与 a a a 做 IoU 运算,若数值大于等于 0.5 0.5 0.5,则将 b b b 从 D D D 中剔除并抛弃;否则保留在 D D D 中并打上标记。
- 若 D D D 中元素未全部被打上标记,则返回 2 继续运行。
- 将 a a a 从 D D D 中剔除并作为一个最终的预测区域输出。
- 若 D D D 中还有元素,则将所有元素的标记清除,然后返回 1 继续运行。
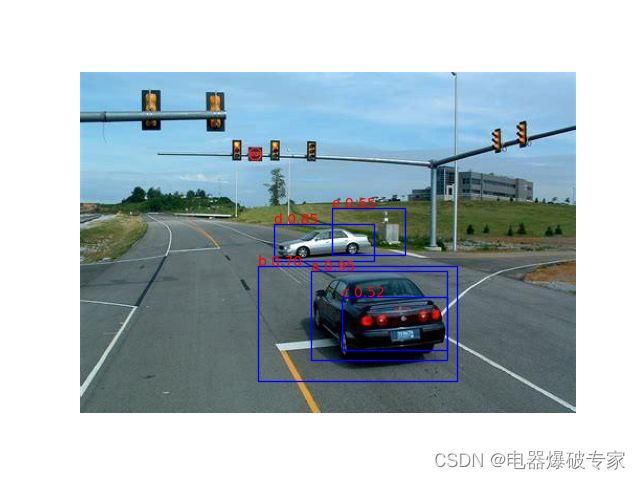
交并比(Intersection-over-Union, IoU):两个区域交叉的面积与合并的面积之比
- 第一轮:选择区域 a 并抛弃区域 b 和 c ,而后将 b 输出。
- 第二轮:选择区域 d 并抛弃区域 e,而后将 d 输出。
Bounding-box Regression
上一步输出的预测框(包围预测区域的框)与真实框(ground truth bounding-box)之间仍然存在些许差距,因此作者使用 Bound-box regression 来对预测框进行修正,使之尽可能的接近真实框。不同类事物的修正方式也是不同的,所以每个类别的事物都有其特定的 BBR。如下图, P P P 是预测框, G G G 是真实框, G ^ \widehat{G} G 是 BBR 对 P P P 修正后生成的预测真实框。

BBR 底层使用了 4 4 4 个线性回归模型,它们都以预测区域在 CNN 中第 5 5 5 个池化层的输出( 9216 9216 9216 维的向量)作为输入,分别预测 d x ( P ) d_x(P) dx(P)、 d y ( P ) d_y(P) dy(P)、 d w ( P ) d_w(P) dw(P) 和 d h ( P ) d_h(P) dh(P) 四个量。这四个量分别与预测框的水平平移、垂直平移、水平缩放和垂直缩放有关。我们将预测框的水平坐标、垂直坐标、水平边长和垂直边长记作 P x P_x Px、 P y P_y Py、 P w P_w Pw 和 P h P_h Ph,预测真实框的对应数据记作 G ^ x \widehat{G}_x G x、 G ^ y \widehat{G}_y G y、 G ^ w \widehat{G}_w G w 和 G ^ h \widehat{G}_h G h,则 BBR 的修正公式如下:
G ^ x = P x + P w d x ( P ) G ^ y = P y + P h d y ( P ) G ^ w = P w exp [ d w ( P ) ] G ^ h = P h exp [ d h ( P ) ] (1) \begin{aligned} & \widehat{G}_x = P_x + P_w d_x(P) \\ & \widehat{G}_y = P_y + P_h d_y(P) \\ & \widehat{G}_w = P_w \exp{[d_w(P)]} \\ & \widehat{G}_h = P_h \exp{[d_h(P)]} & \end{aligned} \tag{1} G x=Px+Pwdx(P)G y=Py+Phdy(P)G w=Pwexp[dw(P)]G h=Phexp[dh(P)](1) 不同预测框的尺寸不一定相同,所以对其进行修正时的位移量也不一定相同,尺寸大的位移量大一些,尺寸小的位移量小一些。所以,作者将 d x ( P ) d_x(P) dx(P) 和 d y ( P ) d_y(P) dy(P) 分别乘以 P w P_w Pw 和 P y P_y Py 作为位移量,这相当于是针对预测框的尺寸做了一个适应性变换。
图像尺寸的缩放系数必须是个正数,而 e x e^x ex 具有恒正和单调递增的特性,所以作者将 d w ( P ) d_w(P) dw(P) 和 d h ( P ) d_h(P) dh(P) 做了指数运算。
训练过程
R-CNN 模型并不是整体进行训练的,而是分模块、分步骤进行训练。模型中需要训练的有 CNN、SVM 和 BBR 三个模块。训练过程按照如下顺序进行:准备正负样本、CNN 预训练(pre-training)、CNN 微调(fine-tuning)、SVM 训练、BBR 训练。
准备样本
针对训练集中的所有图片使用 Selective Search 算法在每张图片上生成 2000 2000 2000 个候选区域(region proposal)。在每张图片上,令所有候选区域分别与真实区域(ground truth)做 IoU 运算,而后记录下来。在训练过程中,作者以 IoU 值作为划分依据,来为不同的模型创造训练样本集。
CNN Pre-training
CNN 模型大、参数多,如果训练集较小,将会导致训练不充分,易发生过拟合。所以作者使用大型的图像分类数据集(ImageNet 比赛数据集)对 CNN 进行预训练,然后将训练好的参数值保存下来。需要注意的是,在训练中 CNN 中的 softmax 输出层并未被 SVM 替换,而是按照一个完整的 CNN 图像分类器进行训练。
CNN Fine-tuning
在完成预训练的基础上,使用我们之前准备的样本再对 CNN 进行训练(仍然不替换 softmax),并使用一个极低的学习率 0.001 0.001 0.001(这是预训练时学习率的十分之一)。这也就是针对我们当前需要的分类任务进行的一个网络微调。
对于训练需要的样本,作者将 I o U ⩾ 0.5 IoU \geqslant 0.5 IoU⩾0.5 的候选区域打上与真实区域相同的类别标签,这被作者称为正样本;其余的被打上背景标签,这被作者称为负样本。 需要注意的是,这些样本需要经过 warp 操作后才能送入网络进行训练。
SVM Training
对于 SVM 的训练样本,作者仅将 I o U = 1 IoU = 1 IoU=1 即真实区域作为正样本;仅将 I o U < 0.3 IoU < 0.3 IoU<0.3 的作为负样本。这些样本需要先经过 warp 操作,再经过 CNN 提取出 4096 4096 4096 维的特征向量,才能用于 SVM 的训练。
下面我们先来回答一下为什么使用 SVM 作为分类器。其实归根结底就是使用 softmax 做分类的效果不理想。首先,softmax 输出层是跟随 CNN 一同进行训练的,CNN 的正负样本划分标准是 I o U ⩾ 0.5 IoU \geqslant 0.5 IoU⩾0.5 和 I o U < 0.5 IoU < 0.5 IoU<0.5,而 SVM 的标准是 I o U = 1 IoU = 1 IoU=1 和 I o U < 0.3 IoU < 0.3 IoU<0.3,所以 CNN 样本的区分度不如 SVM 的区分度大,训练出的效果自然不好。那我们难道不可以将 CNN 的样本区分度做的也大一点?一方面,区分度做大的同时,样本数量也随之减少;样本数量减少,CNN 整体的效果也会被拉低。另一方面,SVM 就是为了小样本集而生的,SVM 在小样本集上的泛化性能要优于其它模型。所以区分度做大,样本集变小是适合于 SVM 的。
此外,作者为了增强分类能力,在训练 SVM 时使用了难负例挖掘(hard negetive mining)方法。
难负例挖掘的基本思路是:在目标检测中负样本的数量是相对较多的,分类器很容易将负样本预测成正样本。所以我们需要挖掘出具有代表性的负样本,即容易让分类器犯错的负样本(难负例),然后让机器反复学习这些负样本。难负例挖掘的过程大致如下:
- 使用正样本集和负样本集的一个子集(负样本训练集)对分类器进行初始训练。
- 让分类器对负样本集进行预测,将分类器预测错误那些负样本加入负样本训练集。
- 使用正样本集和新的负样本训练集再次对分类器进行训练。
- 返回到 2,直到准确率不再提升。
Bounding-box Regression Training
作者仅选用了 I o U ⩾ 0.6 IoU \geqslant 0.6 IoU⩾0.6 的候选框和真实框来训练 BBR。因为只有预测框和真实框十分接近时,我们才可以近似的认为预测框到真实框的修正是线性变换。我们继续使用上文中的符号,并增加 G x G_x Gx、 G y G_y Gy、 G w G_w Gw 和 G h G_h Gh 代表真实框的四个参数。通过上文我们知道,BBR 预测 d x ( P ) d_x(P) dx(P)、 d y ( P ) d_y(P) dy(P)、 d w ( P ) d_w(P) dw(P) 和 d h ( P ) d_h(P) dh(P) 四个量,所以在训练过程中我们需要给出这四个量的目标值 t x ( P ) t_x(P) tx(P)、 t y ( P ) t_y(P) ty(P)、 t w ( P ) t_w(P) tw(P) 和 t h ( P ) t_h(P) th(P),以完成监督训练。下面给出表达式:
t x ( P ) = G x − P x P w t y ( P ) = G y − P y P h t w ( P ) = ln ( G w P w ) t h ( P ) = ln ( G h P h ) (2) \begin{aligned} & t_x(P) = \frac{G_x-P_x}{P_w} \\ & t_y(P) = \frac{G_y-P_y}{P_h} \\ & t_w(P) = \ln{\left( \frac{G_w}{P_w} \right)} \\ & t_h(P) = \ln{\left( \frac{G_h}{P_h} \right)} & \end{aligned} \tag{2} tx(P)=PwGx−Pxty(P)=PhGy−Pytw(P)=ln(PwGw)th(P)=ln(PhGh)(2) 不难看出 ( 2 ) (2) (2) 式实际上就是将 ( 1 ) (1) (1) 式中 G ^ \widehat{G} G 代换成 G G G 并反推 d ∗ ( P ) d_*(P) d∗(P) 的过程。
缺点
- 训练过程复杂。需要分别训练三个模块。
- 训练耗费存储空间。由于三个模块是递进训练的,需要将大量的中间数据存储在硬盘上,作为训练集。
- 处理速度慢。一张图片上有 2000 2000 2000 个候选区域。
- warp 操作使图像失真,降低识别率。
参考文献
R-CNN 《Rich feature hierarchies for accurate object detection and semantic segmentation 》
《目标检测概述》博客
《目标检测算法之R-CNN》博客
《边框回归:BoundingBox-Regression(BBR)》博客
《R-CNN中的SVM理解》博客
《什么是hard negative mining》博客
附录
以下是生成 NMS 章节中示意图的代码:
import matplotlib.pyplot as plt
import matplotlib.image
image = matplotlib.image.imread(r'1.jpeg')
ax = plt.gca()
ax.axis(False)
ax.imshow(image)
def box(axes, x, y, width, height, text):
rect = plt.Rectangle((x, y), width, height, fill=False, color='blue')
axes.text(x, y, text, color='red')
axes.add_patch(rect)
box(ax, 220, 190, 130, 85, 'a 0.95')
box(ax, 170, 185, 190, 110, 'b 0.70')
box(ax, 250, 215, 100, 50, 'c 0.52')
box(ax, 185, 145, 95, 35, 'd 0.85')
box(ax, 240, 130, 70, 45, 'e 0.65')
plt.show()
以下是生成 BBS 章节中示意图的代码:
from matplotlib import pyplot as plt
ax = plt.gca()
ax.axis(False)
rect = plt.Rectangle((0.10, 0.10), 0.60, 0.60, fill=False, color='red')
ax.text(0.4, 0.7, '$P$', color='red')
ax.add_patch(rect)
rect = plt.Rectangle((0.15, 0.15), 0.65, 0.65, fill=False, color='green')
ax.text(0.475, 0.8, r'$\widehat{G}$', color='green')
ax.add_patch(rect)
rect = plt.Rectangle((0.20, 0.20), 0.70, 0.70, fill=False, color='blue')
ax.text(0.55, 0.9, '$G$', color='blue')
ax.add_patch(rect)
plt.show()