datawhale 11月学习——水很深的深度学习：循环神经网络

前情回顾

1. 深度学习概述和数学基础
2. 机器学习基础
3. 前馈神经网络

概述

本次学习结合了李宏毅机器学习的相关章节进行学习，从首先补充了计算图的相关知识，随后，学习了RNN的结构，训练，及可能遇到的梯度消失的问题；再进步学习了LSTM的结构，和例子。同时简单使用torch进行了代码实现。还了解了其他经典的循环神经网络，及其主要应用。

1 计算图

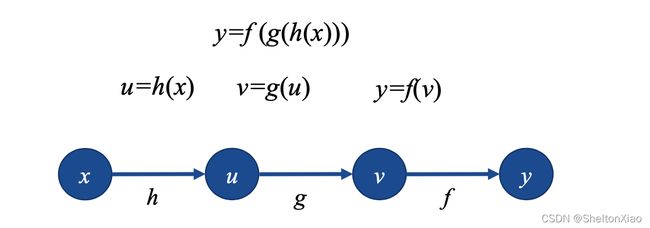
计算图（computation graph）表述了计算过程中各个变量的传递关系及计算过程。

计算图是描述计算结构的一种图，它的元素包括节点(node)和边(edge)，节点表示变量，可以是标量、矢量、张量等，而边表示的是某个操作，即函数。

下图表示复合函数

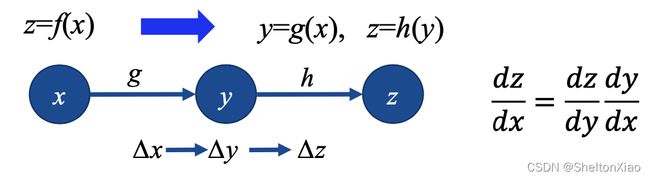
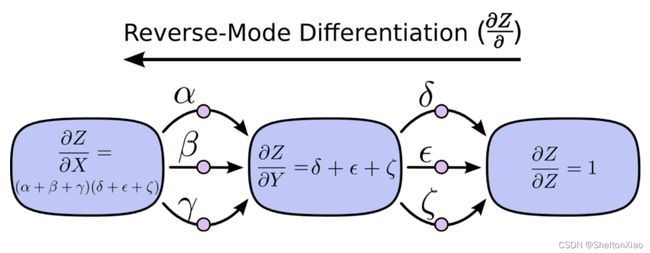
由于反向传播关注求导，我们讨论计算图的求导，可以用链式法则表示，有下面两种情况。

• 情况1
  
• 情况2
  

下图给出了计算图的一个案例

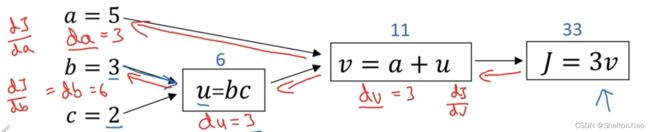
教程里的另一个案例也很好地说明了计算图的传递

前向传播

反向传播

2 RNN

2.1 为什么需要RNN

假设我们现在想要让机器处理一个句子，我们首先要考虑把句子变成向量。

词汇在放入神经网络前，先经过了embedding，变成了一个向量。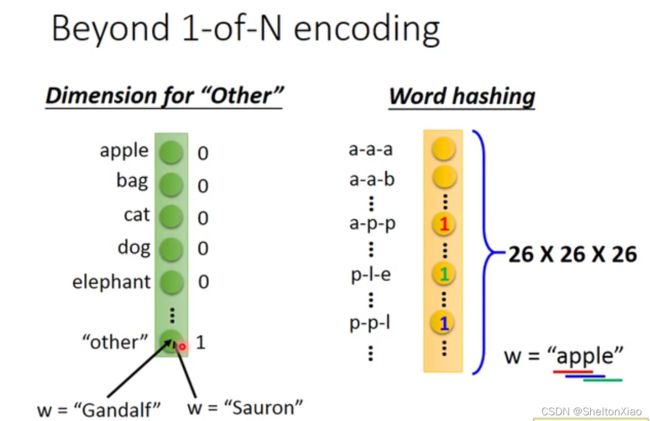
但是，在自然语言处理中，我们容易发现，对于同一个词汇，有可能在不同的句子里代表不同的含义。

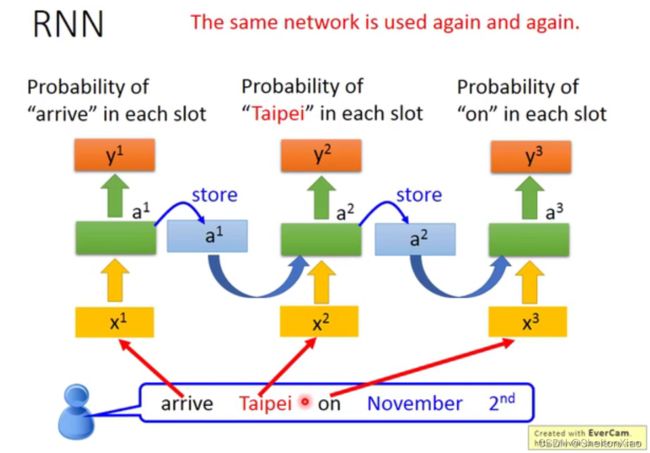
如下图，在第一个句子中，Taipei是目的地，在第二个句子中，Taipei是出发地。

对于一般的神经网络来说，同一个输入对应的输出是一样的，显然不能满足我们的要求。

我们希望我们的神经网络有记忆，根据上下文来判断词性。

循环神经网络由此而生。

循环神经网络的发展历程由下图所示

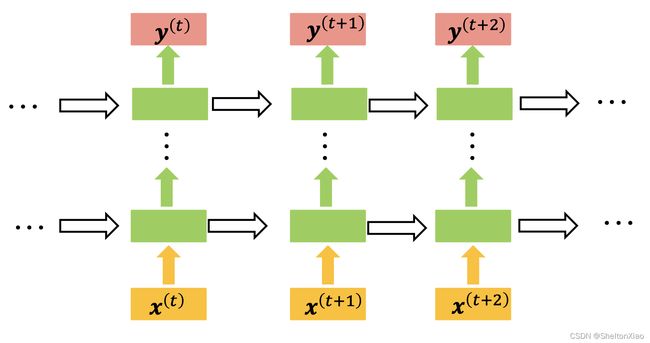
循环神经网络是一种人工神经网络，它的节点间的连接形成一个遵循时间序列的有向图，它的核心思想是，样本间存在顺序关系，每个样本和它之前的样本存在关联。通过神经网络在时序上的展开，我们能够找到样本之间的序列相关性。

RNN的一般结构如下图所示

其中各个符号的表示：$x_t$,$s_t$,$o_t$ 分别表示的是$t$时刻的输入、记忆和输出，$U$,$V$,$W$是RNN的连接权重，$b_s$,$b_o$ 是RNN的偏置，$\sigma$,$\phi$是激活函数，$\sigma$通常选$tanh$或$sigmoid$，$\phi$通常选用$softmax$。

2.2 RNN的简单案例

下图展示了RNN的过程，绿色的会存入蓝色内存中

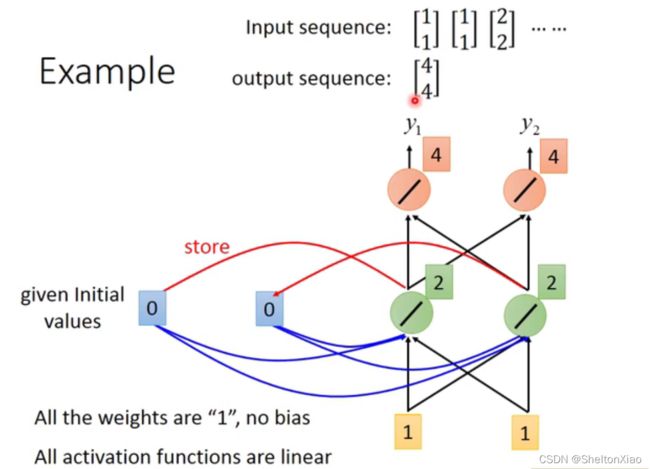
22被存入内存，则此时再输入（1，1），绿色的单元得到1+1+2+2 = 6，就是（6，6）。则输出就是（12，12）。

66被存入内存，洗掉了原来的22，再输入（2，2），此时绿色的单元得到2+2+6+6=16，就是（16，16）。则输出就是（32，32）。

同一个网络在不同的时刻被多次使用。

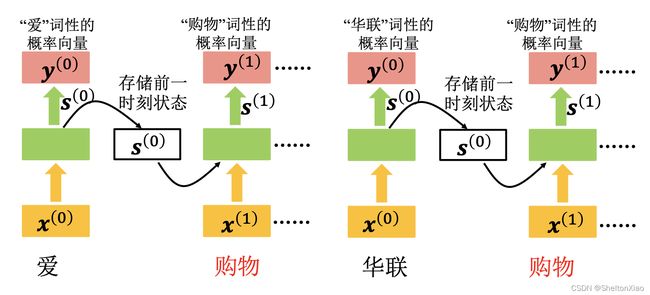
教程里则给出了另一个案例，词性标注的案例。

下图表示了word embedding，词嵌入的过程：

将神经元的输出存到memory中，memory中值会作为下一时刻的输入。在最开始时刻，给定 memory初始值，然后逐次更新memory中的值。

2.3 基础的RNN结构

基础的RNN结构有两种

• Elman Network
  存储的是每个时刻的中间值
  
• Jordan Network
  存储的是上一个时刻的输出
  

各种不同的RNN结构

此外，RNN还可以是双向的

2.4 RNN的训练

是在BP算法的基础上，损失函数对所有t时刻求和。

我们先来回顾一下BP算法，就是定义损失函数 Loss 来表示输出 $\hat{y}$ 和真实标签 y 的误差，通过链式法则自顶向下求得 Loss 对网络权重的偏导。沿梯度的反方向更新权重的值， 直到 Loss 收敛。而这里的 BPTT 算法就是加上了时序演化，后面的两个字母 TT 就是 Through Time。

把所有的损失函数$E$叠加起来，然后分别求对$U$、$V$、$W$的梯度。

$E$对$U$，$V$，$W$的梯度等于每一个$E_1$，$E_2$，…，$E_n$对$U$，$V$，$W$的梯度叠加起来。

其中，求E对W的梯度时，由于不同时刻的$s$之间相互依赖，所以，依赖关系会一直传递到$t=0$的时刻，不能够把上一个时刻的$s$看作是常数项。

2.5 梯度消失

由于损失函数是很多个时刻的叠加，整体的损失函数对于参数的偏导的曲面是很不平整的，会出现很多断崖

会出现好几种情况
第一种：1→2→3跳跃到悬崖上
第二种：1→2→4踩到墙脚
第三种：1→2→4→5加大学习率后直接飞出去

改变w的值就会有使得output的影响变得平缓。

3 长短时记忆网络LSTM

LSTM可以有效解决RNN梯度消失的问题

LSTM和RNN在处理memory cell里面的值的方式不一样：
RNN每次都把新的值存到memory cell里面，旧的值被替换；
LSTM则用了input gate的计算结果与输入相乘后的值累加到memory cell里面。

3.1 LSTM的结构

事实上LSTM的cell对应一个神经元。

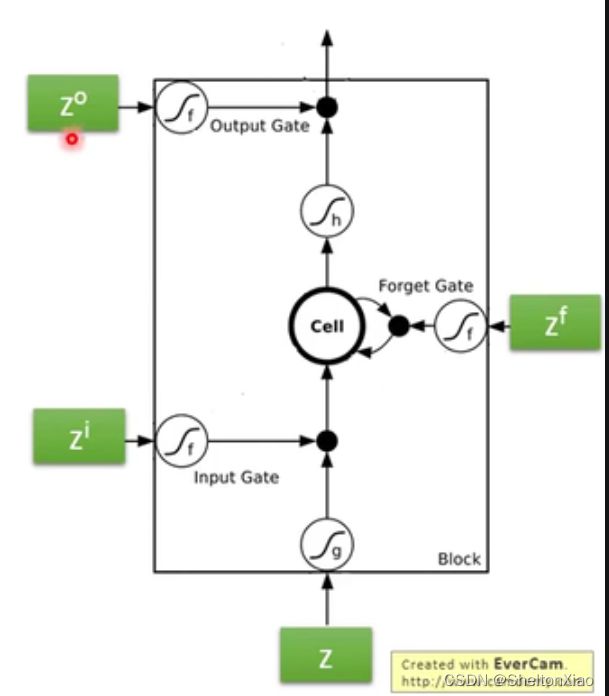
LSTM，即长短时记忆网络，于1997年被Sepp Hochreiter 和Jürgen Schmidhuber提出来，LSTM是一种用于深度学习领域的人工循环神经网络（RNN）结构。一个LSTM单元（cell）由输入门、输出门和遗忘门组成，三个门控制信息进出单元。

由一个输入，三个控制信号输入，和一个输出构成。

• input gate乘以权重，代表当前输入信息的接受权重

• forget gate打开时代表记得，关闭时代表遗忘

• output gate乘以权重，代表当前输出信息的认可权重

LSTM通过门的机制，对状态进行添加或删除，由此实现长时记忆。

3.2 LSTM的例子

对下面这一系列的输入向量，当x2为1时，将x1添加到记忆里；x2为-1时，记忆重设；x3为1时，将记忆里的值输出。

那么下面的图蓝色对应的是记忆中的值，红色对应的是输出值。

对每一个cell，假设有以下场景：

其中，输入门和输出门是常闭的，遗忘门是常开的。（下图中的绿色框是用于乘以权重的输入值）

则对于第一个输入（3，1，0），input gate打开，同时forget gate打开（记住），而output gate关闭，因此3会被存入内存，但不会被输出。

再仔细看一下这个原理

• x2对应的是input gate乘以权重的位置，而input gate是常关的，只有x2为正值时，input gate 会被打开
• x2对应的是forget gate乘以权重的位置，而forget gate是常开的，当x2为负值时，forget gate会被关闭，然后遗忘
• x3对应的是output gate乘以权重的位置，只有当x3有正输入时，output gate才会被打开，才可以输出

3.3 进一步理解LSTM

LSTM需要的参数是一般的四倍



LSTM随着时间是这样变化的

3.4 代码实现

首先实现一个RNN网络

import torch
from torch import nn

#构造RNN网络，x的维度5，隐层的维度10,网络的层数2
rnn_seq = nn.RNN(5,10,2)

可以随机一个输入

#构造一个输入序列，长为6，batch是3，特征是5
x = torch.randn(6,3,5)

out,ht = rnn_seq(x) # h0可以指定或者不指定

可以看一下out和ht的维度

[IN]: out.shape
[OUT]: torch.Size([10, 3, 100])
[IN]: ht.shape
[OUT]: torch.Size([2, 3, 10])

其中rnn输入含义是

Inputs: input, h_0

• input: tensor of shape :math:(L, N, H_{in}) when batch_first=False or
  :math:(N, L, H_{in}) when batch_first=True containing the features of
  the input sequence. The input can also be a packed variable length sequence.
  See :func:torch.nn.utils.rnn.pack_padded_sequence or
  :func:torch.nn.utils.rnn.pack_sequence for details.
• h_0: tensor of shape :math:(D * \text{num\_layers}, N, H_{out}) containing the initial hidden
  state for each element in the batch. Defaults to zeros if not provided.

输出含义是

Outputs: output, h_n

• output: tensor of shape :math:(L, N, D * H_{out}) when batch_first=False or
  :math:(N, L, D * H_{out}) when batch_first=True containing the output features
  (h_t) from the last layer of the RNN, for each t. If a
  :class:torch.nn.utils.rnn.PackedSequence has been given as the input, the output
  will also be a packed sequence.
• h_n: tensor of shape :math:(D * \text{num\_layers}, N, H_{out}) containing the final hidden state
  for each element in the batch.

同样也可以实现一个LSTM网络

#输入维度50，隐层100维，两层
lstm_seq = nn.LSTM(50,100,num_layers=2)

可以随机一个输入

#输入序列seq= 10，batch =3，输入维度=50
lstm_input = torch.randn(10,3,50)

out,(h, c) = lstm_seq(lstm_input)#使用默认的全0隐藏状态

其中lstm的输入含义是

input, (h_0, c_0)

• input: tensor of shape :math:(L, N, H_{in}) when batch_first=False or
  :math:(N, L, H_{in}) when batch_first=True containing the features of
  the input sequence. The input can also be a packed variable length sequence.
  See :func:torch.nn.utils.rnn.pack_padded_sequence or
  :func:torch.nn.utils.rnn.pack_sequence for details.
• h_0: tensor of shape :math:(D * \text{num\_layers}, N, H_{out}) containing the
  initial hidden state for each element in the batch.
  Defaults to zeros if (h_0, c_0) is not provided.
• c_0: tensor of shape :math:(D * \text{num\_layers}, N, H_{cell}) containing the
  initial cell state for each element in the batch.
  Defaults to zeros if (h_0, c_0) is not provided.

输出含义是

output, (h_n, c_n)

• output: tensor of shape :math:(L, N, D * H_{out}) when batch_first=False or
  :math:(N, L, D * H_{out}) when batch_first=True containing the output features
  (h_t) from the last layer of the LSTM, for each t. If a
  :class:torch.nn.utils.rnn.PackedSequence has been given as the input, the output
  will also be a packed sequence.
• h_n: tensor of shape :math:(D * \text{num\_layers}, N, H_{out}) containing the
  final hidden state for each element in the batch.
• c_n: tensor of shape :math:(D * \text{num\_layers}, N, H_{cell}) containing the
  final cell state for each element in the batch.

可以看一下维度

[IN]: out.shape
[OUT]: torch.Size([6, 3, 10])
[IN]: h.shape
[OUT]: torch.Size([2, 3, 100])
[IN]: c.shape
[OUT]: torch.Size([2, 3, 100])

3.5 其他经典的循环神经网络

• Gated Recurrent Unit (GRU)
• Peephole LSTM
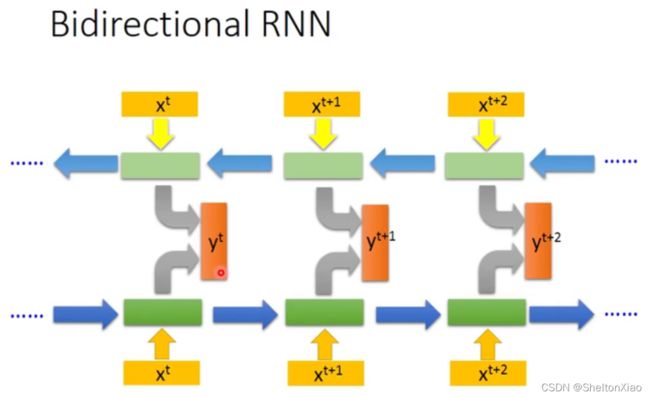
• Bi-directional RNN (双向RNN)
• Continuous time RNN(CTRNN)

3.6 循环神经网络的主要应用

• 语言模型：预测、问答
• 自动作曲
• 机器翻译
• 自动写作
• 图像描述

参考阅读

1.Recurrent Neural Network