生活不如意？不如来学习一下GAN(Generative Adversarial Nets) 论文精读

说明：论文原文Generative Adversarial Nets (nips.cc)，文中图片均来自该论文。

ABS

提出了一种框架（GAN），该框架通过对抗过程来评估生成模型。

框架中有两个模型：生成模型$G$和辨别模型$D$，$G$用来提取数据的分布从而生成人造数据，$D$用来评估样本来自训练数据集的可能性（即样本是真实的可能性）。$G$的目标是让$D$尽可能犯错误（类似于博弈游戏）。在最优情况下，$G$完全吻合原始数据的特性，此时$D$输出的概率全部是$50$。该框架不需要任何的马尔可夫链（条件概率相互依赖）。

1 Intro

基于反向传播的识别算法已经取得了巨大的成功。而深度生成模型因为种种原因并没有取得很好的进展。作者提出了一种能够跨过现有困难的框架的生成模型评估方法——对抗网络（adversarial nets）。

作者举了一个例子：将生成模型$G$比作是一个假币制造者，而把辨别模型$D$比做一个警察。$G$需要尽可能制造难以辨别的假币，$D$需要尽可能的识别假币。两者之间的竞争关系使得$G$的“造假”水平和$D$的辨别能力都能得到提升，在最终情况会期望达到一种平衡（博弈论中叫做纳什均衡，但这里的平衡似乎并那么那是平衡：警察最终无法辨别，而Faker却获得成功）。

$G$和$D$最简单的情况下都是是MLP（多层感知机），文中的$G$将的输入初始是一个随机的高斯分布，通过训练让$G$（通过调整MLP的参数）能使输出数据尽可能的接近真实数据。过程中使用了反向传播和dropout。

2 Related work

其他工作中大多数都是基于最大似然估计进行推理。

而生成随机网络（不需要马尔科夫链）可以生成想要的样本。

作者指出自己的工作与VAEs（variational autoencoders）有一定的相似之处，但是不完全相同。

NCE（Noise-contrastive estimation）也训练识别模型，但是识别模型由噪声分布和模型分布的概率密度的比率来定义（这样定义需要能够同时对两个模型进行评估和反向传播）。

predictability minimization中也有两个网络，但是不同于GAN，第一个网络中的隐藏单元会尽可能的输出与另一个网络不同的输出，而另一个网络的隐藏层会尽可能地输出与第一个网络相同的输出。

3 Adversarial nets

以标量为例，来说明两个网络需要做的事情，首先我们需要定义一些符号：

• $x$表示真实数据；
• $p_{data}$表示真实数据的概率密度；
• $p_g$表示$G$最终学习到的概率密度；
• $p_z$表示$G$初始概率密度（一般是一个高斯分布）；
• $G(z;{\theta }_g)$表示生成网络的输出（本文使用MLP，${\theta }_g$是MLP的参数，$D$中参数同理）；
• $D(x;{\theta }_d)$表示辨别网络的输出，该输出表示$x$（这里的$x$仅仅表示$D$的输入）来自真实数据的概率。

正如前面介绍的，两个网络有着各自的目标：

• 辨别网络$D$的目标：当输入是真实数据是，输出应该尽可能靠近$1$；当输入是人造数据时，输出应该尽可能的靠近0。
• 生成网络$G$的目标是：生成的数据让辨别网络的输出尽可能的靠近$1$，这里我们转换成最大化：$log(1-D(G(z)))$，也就是让$D(G(z))$尽可能的靠近$1$。

对于$D$和$G$的目标可以用一个方程来表示：

$\underset{G}{\min }\underset{D}{\max }V(D,G)=E[logD(x)]+E[log(1-D(G(z)))](1)$

上述公式需要拆开来看：

• 对于$G$，需要$min(E[logD(x)]+E[log(1-D(G(z)))])=min(E[log(1-D(G(z)]$，这是因为对于$G$来说能产生联系的是$z$而不用关心$x$；
• 对于$D$，需要$max(E[logD(x)]+E[log(1-D(G(z)))])$。

实际的训练：

• 直接最优化$D$是行不通的，这很容易导致过拟合，作者提出了一种训练方法通过对$D$进行$k$次优化的同时加入对$G$进行一次优化，这样让两个网络同时进行训练，只要$G$更新的足够慢，$D$就会收敛到最优解，整个算法过程如Algorithm 1所示。
• 在训练一开始由于$G$生成的数据非常不好，$D$有很大的概率直接让$log(1-D(G(z)))$等于0，这样进行反向传播的时候，$G$会非常难训练（梯度一开始会非常小），所以采用了一种转换：在训练的时候让$G$去最大化$log(D(G(z)))$。

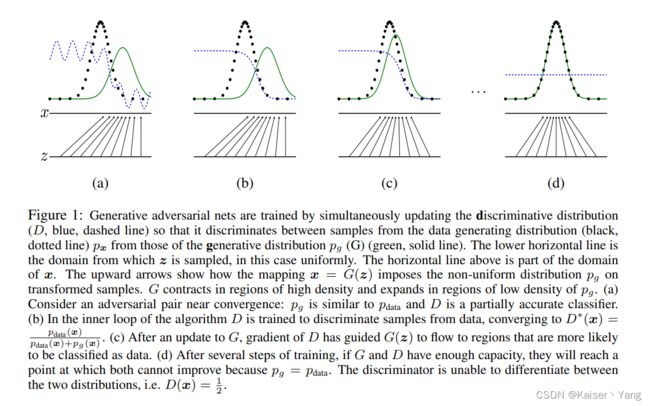Figure 1是Algorithm 1的一个简单情况的可视化：

• 绿色的线代表$G$生成的数据，黑色的点代表真实的数据，蓝色虚线代表$D$的输出；
• 在一开始$G$会生成一个高斯分布这个分布与真实数据差距较远，而$D$的能力较差，预测结果存在震荡情况，如（a）所示；
• 此时对$D$进行$k$次的优化，理想情况下$D$会收敛（收敛的具体值在下一小节中证明），如（b）所示；
• 此时对$G$进行$1$次优化，会使得输出更加靠近真实值，如（c）所示；
• 在最终的情况下，两者会到一种平衡状态，此时$D$的输出始终是$\frac{1}{2}$而$G$的输出与真实值完全一样，如（d）所示。

4 Theoretical Results

4.1 Global Optimality of $p_g=p_{data}$

存在全局的最优解$p_g=p_{data}$，下面进行详细的说明。

Proposition 1：当$G$固定时，对于$D$存在最优解：
$$D_G^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}(2)$$
上面的公式很好理解，下面进行证明：

最优解就是让$V(G,D)$最大的点，而：
$$\begin{array}{rl}V(G,D)& ={\int }_x{p}_{data}(x)log(D(x))dx+{\int }_z{p}_z(z)log(1-D(G(z)))dz\\ & ={\int }_x{p}_{data}(x)log(D(x))+p_g(x)log(1-D(x))dx(将z看成x的函数z(x))(3)\end{array}$$
而$p_{data}(x)log(D(x))+p_g(x)log(1-D(x))$的最大值在$D(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$处取得（因为$alog(y)+blog(1-y)$的最大值在$y=\frac{a}{a+b}$处取得，其中$0\le y\le 1,a+b\ne 0,a\ge 0,b\ge 0$）。

将（2）带入（1）中我们可以得到：
$$\begin{array}{rl}C(G)& =\underset{D}{m}axV(G,D)\\ & =E_{p_{data}}[log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E_{p_g}[\frac{p_g(x)}{p_{data}(x)+p_g(x)}](4)\end{array}$$
Theorem 1：当且仅当$p_g=p_{data}$时$C(G)$取最小值$-log4$，即$G$此时达到最优。

证明需要用到一些统计的知识：K-L散度和J-S散度
$$\begin{array}{rl}C(G)& =-log4+E(log2)+E_{p_{data}}[log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E(log2)+E_{p_g}[\frac{p_g(x)}{p_{data}(x)+p_g(x)}]\\ & =-log4+KLD(p_{data}||\frac{p_{data}+p_g}{2})+KLD(p_g||\frac{p_{data}+p_g}{2})\\ & =-log4+2JSD(p_{data}||p_g)\end{array}$$
J-S散度是一个非负数，当且仅当$p_{data}=p_g$时取$0$所以上式的最小值位$-log4$（G的目标是取最小值）。

注：
$$\begin{array}{rl}& KLD的定义：KLD(p||q)=E_p(log\frac{p}{q})=\int p(x)(logp(x)-logq(x))dx\\ & KLD性质：（1）非负；（2）非对称性：KLD(p||q)\ne KLD(q||p)\\ & JSD的定义：JSD(p||q)=\frac{1}{2}(KLD(p||m)+KLD(q||m))其中m=\frac{p+q}{2}\\ & JSD性质：（1）非负；（2）对称性\end{array}$$

4.2 Convergence of Algorithm 1

Proposition 2：在算法1的过程中只要$D$在过程能够到达最优解，那么$p_g$会收敛于$p_{data}$，证明略。

即使在实际的训练中我们并没有更新$p_g$而是更新MLP的参数，但是这同样可以获得不错的表现。

5 Experiments

在MNIST，TFD，CIFAR-10上做了实验。实验结果如Table 1所示（表格中的数字越大，效果越好）：

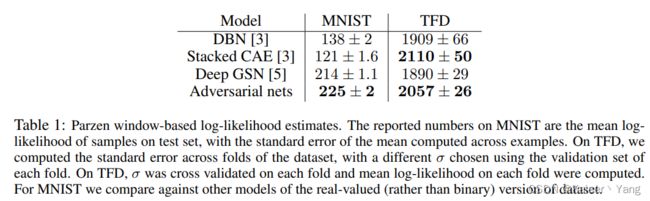
Figure 2展示了生成的图片（最右边应该是真实数据）。

Figure 3表示：两张图的的最左边和最右边的数字时真实的，中间的数字是通过线性插值生成的。

6 Advantages and disadvantages

缺点：

• 并没有直接给出$p_{data}$；
• 训练过程中要求$D$和$G$同步更新，对于调参来说不太容易；

优点：

• 不需要马尔可夫链；
• 在训练过程不需要推理；
• G的反向传播并不依照真实数据进行而是根据D来进行；
• 能拟合退化的分布（或噪声比较强）。

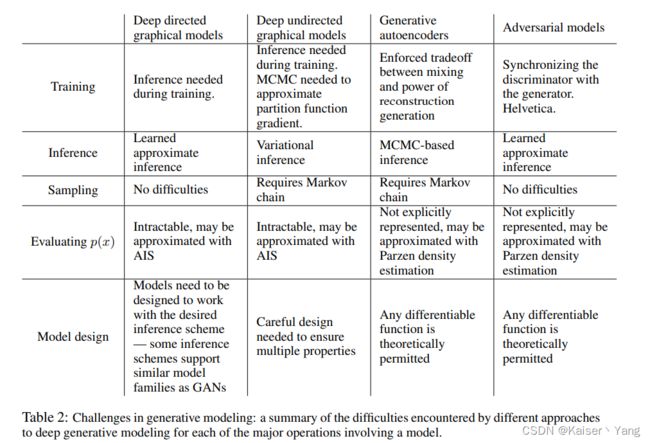
Table 2是一份详细的总结，第一行是模型名称，第一列是方面。

7 Conclusion and future work

可以增加的拓展：

• 可以通过对$G$和$D$增加输入来训练条件概率分布；
• 可以通过训练一个备用网络对于给定的$x$预测$z$来进行近似推理（approximate inference）；
• 可以训练多个条件下的条件概率分布；
• 当有标记的数据有限时，辨别器所识别的特点能够提升分类的效果；
• 通过更好的方法来协调$G,D$可以加快训练速度。