DeepWalk究竟是什么?为什么图神经网络要学习它?DeepWalk论文精读
本文是精读DeepWalk后做出了一些简略说明与解读。
原文链接:DeepWalk: Online Learning of Social Representations。
文章中的图片均来自论文原文。
ABS
依据NLP和Random-Walk提出了一种对社交关系网络进行隐编码的方法:DeepWalk。
DeepWalk利用随机游走形成的局部信息(将每一次游走得到的信息看成是一个句子)来学习网络的表示。
作者通过DeepWalk做了一些图的多分类问题,得到的效果非常好。
该算法有以下几个优点:
- 可以扩展
- 可以增量学习
- 可以很容易地实现并行。
1 INTRO
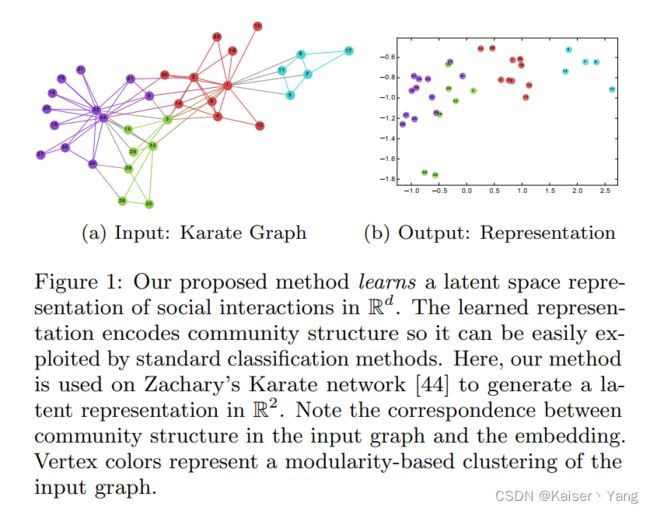
通过随机游走结合NLP相关的处理,提出了DeepWalk,将该方法运用到Karate network(一个空手道俱乐部的人员关系网络)中,将每个节点编码成一个二维的向量,可以得到Figure 1的结果,(a)代表输入的网络,不同的颜色代表不同的类别,(b)代表的是将节点的向量表示绘制到一个平面图上,可以看到同一类节点的编码在图中相对比较密集。
文章进行了一些实验,实验中作者将DeepWalk应用到大量不同图的多分类问题上。
在关系分类(Relational Classification)问题中,之前的方法违背了i.i.d.(独立同分布)假设,解决方法一般是使用近似推理(Approximate Inference,进行近似推理的原因是:Exact Inference是NP-hard问题)。而Deep Walk并不使用近似推理,而是学习图的标签独立表示。
当被标记的节点是稀疏的时候,DeepWalk能够取得特别好的效果(通过后续的实验可以看到,当DeepWalk仅获得部分信息时能够获得很好的效果)。同时Deep Walk可以很容易的和其他的分类算法进行混合使用,同时可以很容易的实现并行。
本文的贡献:
- 通过使用深度学习来分析图从而建立起图中结点“靠谱”的编码。
- 将本文模型用于多分类问题。性能提升明显。
- 通过建立web-scale图(注1)的表示来展示该方法的可拓展性。
注1:文章并没有说明什么是web-scale,只是举例YouTube是web-scale图,这里网上也没有找到定义。
2 PROBLEM DEFINITION
考虑二分类或者多分类问题。首先给出一些定义:
-
V V V:代表图的顶点;
-
E E E:代表图的连接关系(边);
-
G = ( V , E ) G=(V,E) G=(V,E):代表一张图,顶点为 V V V边为 E E E;
-
X X X: X ∈ R ∣ V ∣ × S X\in R^{|V|\times S} X∈R∣V∣×S(其中 S S S是特征的维度)是属性(features);
-
Y Y Y: Y ∈ R ∣ V ∣ × ∣ y ∣ Y \in R^{|V| \times |y|} Y∈R∣V∣×∣y∣(其中 y y y是输出(labels)的集合)代表输出;
-
G L = ( V , E , X , Y ) G_L=(V,E,X,Y) GL=(V,E,X,Y):一个带有标记的社交网络。
该分类问题即关系分类,传统的解决方法是通过将问题看成一个非直连的马尔可夫网络,使用迭代近似推理或者根据给定的网络计算输出的后验分布。
本文采用的方法不需要考虑输出的分布,能够直接从图的结构中学习到特征(无监督学习)。
目标:学习 X E ∈ R ∣ V ∣ × d X_E \in R^{|V|\times d} XE∈R∣V∣×d,其中 d d d是一个比较小的数。可以用该向量和各类分类算法一起完成分类任务。
3 LEARNING SOCIAL REPRESENTATIONS
模型学习遵循的特点:
- 适用性:社交网络一直在变化,因此不希望一点变化就让模型重新学习(模型可以增量学习);
- 能够发觉到强关联的点:两个顶点学习出来的向量的距离应该能够评估两个人的社会相关性;
- 低纬度:学习出来的向量维度应该较低,这样在标签缺少的情况下,效果会更好;
- 连续性:学习到的向量应该属于连续空间,连续性使得边界处更加平滑能够适应更多的分类问题。
3.1 Random Walks
随机游走(Random Walk):从一个起始结点开始,随机地到达邻居结点,一共执行 k k k次叫做 k k k-随机游走,期间会形成顶点序将此顶点序列记作: W v i = [ W v i 1 , W v i 2 , . . . , W v i k ] W_{v_i} = [W_{v_i}^1,W_{v_i}^2,...,W_{v_i}^k] Wvi=[Wvi1,Wvi2,...,Wvik]其中 v i v_i vi为起始节点。
使用随机游走的好处:
- 多次随机游走很容易并行;
- 当图发生微小的改变时,可以不用全部重新计算,只需要在改变的区域进行随机游走即可。
3.2 Connection: power laws
power law distribution(i.e. scale-free):某个量是另一个量的幂次方,文章这里指的是平时所熟知的二八定律,以经济占有为例:即 20 % 20\% 20%(少量)的人掌握了 80 % 80\% 80%(大量)的财富,剩下 80 % 80\% 80%(大量)的人掌握了剩下 20 % 20\% 20%(少量)的财富。
作者发现:如果节点度数的分布符合power law分布(指某些少量节点的度数很大,而大量节点的度数很小),那么一个节点在随机游走中出现的频率也符合power law分布(少量节点的出现次数很多,大量节点出现次数很少),这一点与自然语言中词语使用频率类似。
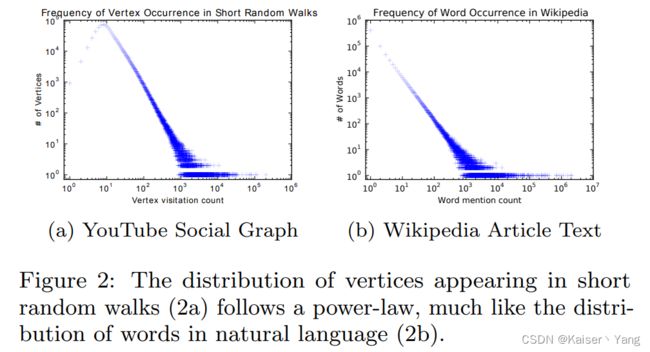
Figure 2展现了随机游走序列中的二八定律与NLP中的二八定律类似(纵坐标代表出现的频率,可以看到少部分的点(词语)出现的频率很高,而大部分的点(词语)出现的频率很低)。
本文的重要贡献之一就是发现了NLP利用“二八定律”的方法可以被用在处理社交网络中。
3.3 Language Modeling
语言模型的目标是评估对于给定一个序列下一个单词的可能性(例如翻译模型就是给定一个序列根据输出的可能性,选择下一个词语)。
而本文中作者将随机游走序列转换成一个语言处理模型:给定一个随机游走序列,需要计算出到达每个节点的可能性。
除了需要计算可能性之外,还需要学习每个节点的表示,于是作者提出了一个映射函数 Φ \Phi Φ: v ∈ V − > R ∣ V ∣ × d v\in V->R^{|V|\times d} v∈V−>R∣V∣×d(将顶点映射成一个向量,该函数通过矩阵乘法实现),上面提到的预测问题变为给定顶点向量预测下一个顶点向量的可能性。
近期语言模型发生了改变:由原来的的给定上下文预测单词,变成了给定单词预测上下文(此处的上下文包括上文和下文)。对应在随机游走中的预测就是给定一个点,改点作为随机游走中的一个节点预测整个随机游走序列,即:
m i n i m i z e Φ { − l o g P r ( { v i − w , . . . , v i + w \ v i } ∣ Φ ( v i ) ) } ( 3 ) \underset {\Phi}{minimize}\{ -logPr(\{v_{i-w},...,v_{i+w}\backslash v_i\}|\Phi(v_i))\}\quad (3) Φminimize{−logPr({vi−w,...,vi+w\vi}∣Φ(vi))}(3)
这样的任务非常适用于社交网络,这是因为:
- 顺序独立性假设能够更好的捕捉随机游走提供的近似关系;
- 能够加速训练(可以构件很小的模型,因为每次只有一个节点作为输入)。
4 METHOD
4.1 OVERVIEW
需要的输入是语义表(或者词汇) V V V。DeepWalk将顶点看成是词汇。作者指出一开始知道每个词语的频率(在随机游走序列中的频率)是有好处的,但是本文的算法可以在不知道频率的情况下进行。
4.2 Algorithm: DeepWalk
算法由两部分组成:随机游走生成器和更新的过程。
实际中进行 γ \gamma γ轮的随机游走,每一轮都在每个节点开始长度为 t t t的随机游走。

算法过程如Algorithm 1所示。
4.2.1 SkipGram
LIne 3的概率通过Hierarchical Softmax获取概率。
4.2.2 Hierarchical Softmax
这里实际上不需要掌握Hierarchical Softmax具体怎么计算,文章直接给出整个过程中使用的详细公式。
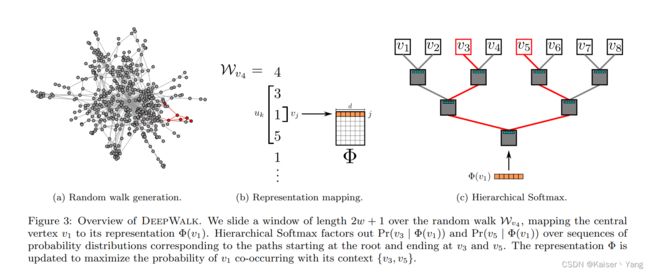
Figure 3是整个DeepWalk的过程,(a)是随机游走的过程,(b)对随机游走产生的序列进行处理,(c)是通过Hierarchical Softmax计算条件概率。
本文提到使用Hierarchical Softmax将上下文问题转换成在路径上走向某个叶节点的概率(每个叶节点代表一个顶点,组成一课完全二叉树)。直接按照如下公式即可获得概率:
P r ( b l ∣ Φ ( v j ) ) = Π l P r ( b l ∣ Φ ( v j ) ) l 表示树上路径经过的点 P r ( b l ∣ Φ ( v j ) ) = 1 1 + e − Φ ( v j ) Ψ ( b l ) Ψ ( b l ) ∈ R d 代表 b l 的父亲的向量表示 \begin{align*} &Pr(b_l|\Phi(v_j)) = \Pi_lPr(b_l|\Phi(v_j))\\ &l表示树上路径经过的点\\ &Pr(b_l|\Phi(v_j))=\frac 1 {1 + e^{-\Phi(v_j)\Psi(b_l)}}\\ &\Psi(b_l)\in R^d代表b_l的父亲的向量表示 \end{align*} Pr(bl∣Φ(vj))=ΠlPr(bl∣Φ(vj))l表示树上路径经过的点Pr(bl∣Φ(vj))=1+e−Φ(vj)Ψ(bl)1Ψ(bl)∈Rd代表bl的父亲的向量表示
这样做可以将复杂度变成 l o g ∣ V ∣ log|V| log∣V∣级别。
同时为了进一步提升速度可以使用哈夫曼编码树(将出现频率作为编码依据)。
4.2.3 Optimization
使用SGD和反向传播,初始学习率是0 . 025 .025 .025,学习率随着已知节点(迭代过程中会逐渐遍历到节点)的增加而减少。
4.3 Parallelizability
可以使用异步SGD,由于更新会很稀疏(因为power law的原因,大部分节点出现的次数很少)在访问共享参数时可以不需要锁。
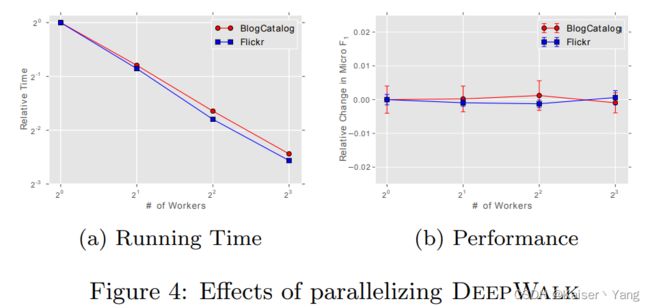
Figure 4展现了并行的结果,不同颜色的线条代表不同的任务;(a)的横坐标代表线程数(可以认为处理器数量大于线程数量)随着线程数量的增加,训练时间下降;(b)代表使用并行后的效果和串行的效果对比,图像表示效果基本没有变化。
4.4 Algorithm Variants
4.4.1 Streaming
在获得随机游走序列时立即进行概率的计算和更新而不是知道整张图的随机游走序列再进行更新。
该方法与Algorithm 1的不同之处:
- 该方法要求一开始知道顶点的个数,所以学习率采用线性下降就没有必要,而是应该固定在一个比较小的值。
- 由于是依次获得随机游走序列,一般情况下不能再使用哈弗曼编码,但是如果一开始能够评估每个节点的出现频率(例如根据节点的度数进行评估),依然可以使用哈弗曼编码。
4.4.2 Non-random walks
不再使用随机游走,而是按照某些提示进行特定的跳动获取序列。这样做能够提取网页中的特定信息,同时该方法可以和Streaming进行结合。
5 EXPERIMENTAL DESIGN
5.1 Datasets
介绍本文使用的数据集:
- BLOG CATALOG:一个社交网络,每个节点代表一个作者,标签代表作者类型;
- FLICKR:一个照片网站的用户关系,标签代表用户的喜好照片类型;
- YOU TUBE:用户和创作者之间的关系。标签代表用户喜欢的视频类型。
5.2 Baseline Methods
作者将自己的方法和以下的方法进行的对比(注2):
- Spectral Clustering
- Modularity
- Edge Cluster
- wvRN
- Majority:输出出现最多的标签
注2:这些方法不是本篇论文的重点,这里不做介绍。
6 EXPERIMENTS
6.1 Multi-label Classification
直接给出在三个数据集上不同的方法训练结果:
(表格中Labeled Nodes表示将图中多少的数据用于训练,剩下的数据用于测试;图中的Micro-F1与Macro-F1均是越高代表效果越好)
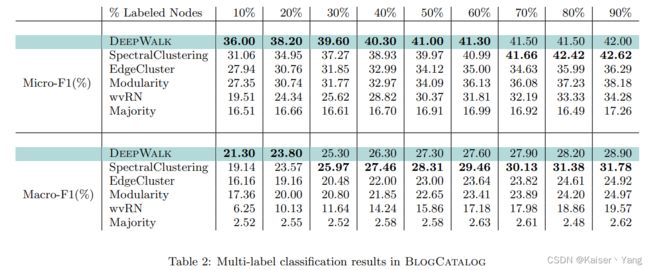
Table 2表示在Blob Catalog上的训练结果,可以看到DeepWalk在获得 10 10% 10数据的时候训练结果比一些模型获得 90 90% 90数据的训练结果还好。
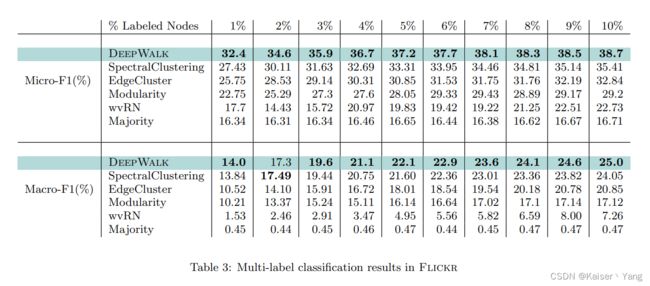
Table 3表示在Flickr上的训练结果。
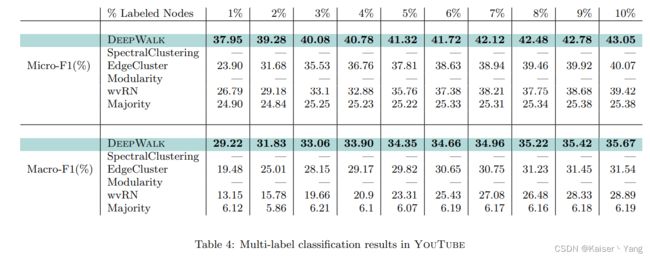
Table 4表示在YouTube上的训练结果。
6.2 Parameter Sensitivity
该部分说明参数的不同对实验效果的影响。
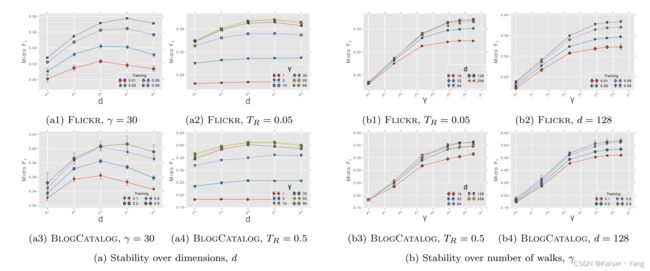
Figure 5是改变参数后的实验结果。
d d d代表的是表示向量的维度, γ \gamma γ是Algorithm 1中的迭代次数。
图中的Training和 T R T_R TR代表用于训练的样本占比。
从图中可以看出来该算法对于 d d d不那么敏感而对于迭代次数 γ \gamma γ是比较敏感的。
7 RELATED WORK
本文的方法与之前方法不同可以总结为以下几点:
- 通过训练获取特征,而不是依照统计的方法获取;
- 没有尝试拓展分类的过程;
- 仅仅使用局部信息的在线算法,大多数其他算法需要全局信息;
- 使用无监督学习。
7.1 Relational Learning
介绍了一下Relational Learning使用的方法。
7.2 Unsupervised Feature Learning
介绍了无监督学习近年来在CV,speech recognition,NLP的应用。
8 CONCLUSIONS
总结了文章提出的方法的特点:在线,可扩展,NLP模型,随机游走。
未来打算的工作:提升语言处理,加强该方法的理论的证明。
