LSTM为什么晦涩难懂？Long Short-term Memory 万字解析 论文精读 LSTM的提出

说明：本文是自己阅读Long Short-term Memory期间，发现论文中的公式复杂，于是写了这篇文章进行梳理，同时给出自己的总结方法。
文中的非手绘图片均来自论文Long Short-term Memory。

注意：此篇文章提出的LSTM并不是现在所熟知的LSTM（现在是指2022年），现在的LSTM拥有Forget Gate，但是这篇文章并没有遗忘门，而带遗忘门的LSTM是出自Learning to Forget Continual Prediction with LSTM(LSTM with Forget Gate)，这篇文章发表自1999年，是对Long Short-term Memory的改进。

ABS

文章说明由于梯度爆炸、（特别是）梯度消失的原因，RNN在记录长期记忆，进行反向传播时耗时巨大、效果差。于是提出了LSTM解决这个长期记录的问题。LSTM训练的更快，能够更好的解决复杂问题和长延时(输出依赖两个时间间隔很久的输入)任务。

1 INTRO

现阶段的算法没有很好的解决长延时任务。作者写这篇文章会分析问题和提出一种解决方法。

问题：梯度爆炸、梯度消失。LSTM可以解决长延时任务使用RNN时梯度爆炸和梯度消失的问题。

2 PREVIOUS WORK

这一部分全部在说之前的所有模型存在的问题，目的是为了引出LSTM，此处不做详细介绍。

3 CONSTANT ERROR BACKPROP

这一部分是介绍传统的BPTT（Backpropogation Through Time，这里指的是在RNN上的反向传播）为什么会出现梯度爆炸、梯度消失的问题，同时提出一种解决方法的雏形。

3.1 EXPONENTIALLY DECAYING ERROR

3.1.1 Conventional BPTT

简单介绍了传统的BPTT出现的问题，这一部分的公式写的比较混乱，各种命名也没有说清楚，下面给出另一种方式说明RNN存在的问题。

首先给出一个简单的RNN模型：

模型中的计算公式如下：

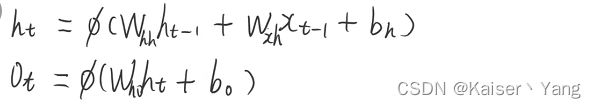
图片中的$\varphi$是一个激活函数。

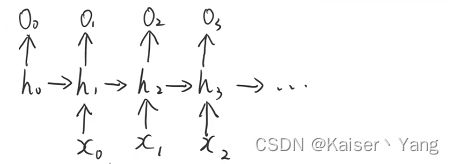
下面来说明这样一个RNN模型在处理长时间间隔问题时存在的问题，在BPTT中（也就是所谓的反向传播），我们需要计算偏导数，这里我们以更新$W_{xh}$为例，对于$t$时刻我们一共有$t$条反向传播的路径，以t=3为例，存在的路径是：

• $o_3->h_3->x_2$
• $o_3->h_3->h_2>x_1$
• $o_3->h_3->h_2->h_1>x_0$

我们将$x_t$出的权重记作$W_{xh}^{(t)}$（这里不同$x$使用的权重矩阵实际上是同一个）在进行前向传播时有：
$$h_3=W_{hh}{h}_2+W_{xh}{x}_2=W_{hh}(W_{hh}h1+W_{xh}{x}_1)+W_{xh}{x}_2=W_{hh}(W_{hh}(W_{hh}{h}_0+W_{xh}{x}_0)+W_{xh}{x}_1)+W_{xh}{x}_2$$
（为了增加可读性，这里暂时不考虑偏差）
可以看到不同时刻的$x$的系数矩阵出现了相加的情况，根据求导的法则，我们在求导的时候也是相加的关系，此时对于$t$时刻有：

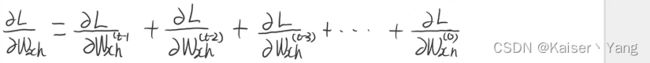
我们将每个时刻的导数根据反向传播的路径展开有：

同时根据$h_t$的计算公式我们可以得到：


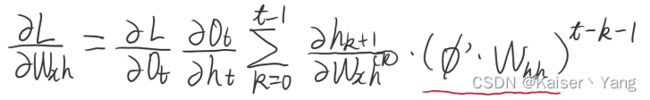
（将上式记作equation (2)）。

3.1.2 Outline of Hochreiter’s analysis

对于equation (2)中的红线勾画部分，可以发现：当$t$增加时，图中的指数项的次数会在$k=0$的时候得到最大值：$t-1$，即距离当前位置越远，对应的导数项的指数的次数越大。

3.1.3 Intuitive explanation of equation (2)

equation (2)表明了两种特殊情况：

• ${\varphi }^{\prime }{w}_{hh}>1.0$，容易出现梯度爆炸（梯度随着$t$的增长指数级别增长）
• ${\varphi }^{\prime }{w}_{hh}<1.0$，容易出现梯度消失（梯度随着$t$的增长指数级别减少）

作者举了一个例子，如果上面的$\varphi$是Sigmoid函数，那么${\varphi }_{max}^{\prime }=0.25$，推导如下：

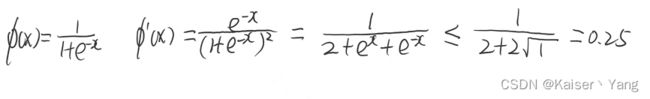
如果$|w_{hh}|<4.0$那么${\varphi }^{\prime }{w}_{hh}<1.0$一定成立，这就很容易发生梯度消失，而作者指出如果简单的增大$w$并不会发生改变（虽然权重增加了，但是${\varphi }^{\prime }$又会很快的趋近于0，这里根据${\varphi }^{\prime }$的表达式可以发现，输入增大，导数值会趋向于0）。

上面的推导过程说明了，对于传统RNN的BPTT，相距当前距离较远的地方的梯度会变得非常小，导致很难学习到长时间间隔任务的特点，这也解释了为什么传统的RNN在长时间间隔问题上面效果不好。

3.1.4 Global error flow

由于局部的梯度消失，导致全局的梯度中不能记住长时间间隔的梯度，导致RNN效果不好。

3.2 CONSTANT ERROR FLOW: NAIVE APPROACH

作者在这一节提出了一个简单的解决方法，我们只需要让${\varphi }^{\prime }{w}_{hh}$ 非常接近于$1$，甚至是等于$1$，这样就能够让传统的RNN不在受梯度消失或者梯度爆炸（这里主要是指梯度消失，因为梯度爆炸可以通过其他的手段来解决例如梯度裁剪，在实际中主要问题也是梯度消失）的影响了。

如果我们让${\varphi }^{\prime }{w}_{hh}=1$，我们对两边积分就可以得到$\varphi$的表达式：$\varphi (x)=\frac{x}{w_{hh}}$

对于最简单的情况，我们可以让$w_{hh}=1$就有：$\varphi (x)=x$

作者将这一步叫做CEC（Constant Error Carrousel）。

作者提出这样做存在两类问题：

• 输入权重冲突（Input Weight Conflict）：对于一个输入，此时权重会发生两种作用：（1）对输入进行提取特征（权重远离0）（2）对之前保存的信息进行尽可能的保存（权重靠近0）。这两种作用对于一个权重来说是冲突的。
• 输出权重冲突（Output Weight Conflict）：在输出时，参数同样有两种作用：（1）从当前状态提取信息（权重远离0）（2）防止当前的信息对其他的单元影响，也就是需要屏蔽信息（权重靠近0）。这两种状态对于一个权重来说同样是冲突的。

4 LONG SHORT-TERM MEMORY

为了解决上述提出的问题，作者提出了LSTM，要想知道LSTM，就要先明白记忆细胞（Memory Cell)，记忆细胞的结构如Figure 1所示：

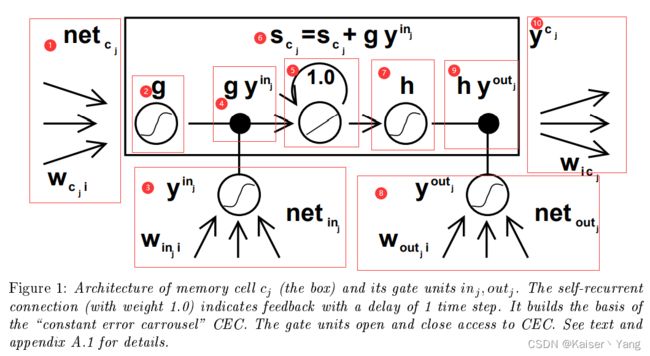
图中有两个重要的概念：

• 输入门单元（input gate unit）：Figure 1中3代表输入门单元。
• 输出门单元（output gate unit）：Figure 1中输入8表输出门单元。

（此篇作者提出的LSTM并没有Forget Gate，带Forget Gate的LSTM是出自Learning to Forget Continual Prediction with LSTM(LSTM with Forget Gate)，带有Forget Gate的LSTM是对该模型的改进）

对于Figure 1的解释：

• Figure 1整体由三部分组成：输入部分（1、3、8）、中间计算部分（2、4、5、6、7、9）和输出部分（10）
• 1：1向记忆单元输入的是$ne{t}_{c_j}$，而$ne{t}_{c_j}$上一时刻的单元输出的加权和，单元$i$（权重为）$W_{c_{j}i}$。
• 2：2代表将$g$作用于输入，即4得到的输入是$g(ne{t}_{c_j})$，类似的还有7和3、8中的符号。
• 3：3代表输入门单元，与1类似，此时会向记忆单元输入$y^{i{n}_j}$，而$y^{i{n}_j}=f(ne{t}_{i{n}_j})$，其中的$ne{t}_{i{n}_j}$也是由上一时刻的单元输出的加权和
• 4：此处代表将两个输入做一次乘法
• 5：代表一次自连接，计算的公式如6
• 7：将$h$作用于5的输出，与2同理
• 8：与3同理
• 9：代表将两个输入做一次乘法，与4同理
• 10：$y^{c_j}$代表的是记忆单元的输出，而记忆单元后面同样可以连接其他记忆单元（将多个记忆单元拼接成一个记忆细胞块，Memory Cell Block），所以此输出可以作为其他单元的输入

上述过程的公式描述：

• 1: $ne{t}_{c_j}(t)={\sum }_u{w}_{c_j}{y}^u(t-1)$
• 2: $g(ne{t}_{c_j}(t))$
• 3: $y^{i{n}_j}(t)=f(ne{t}_{i{n}_j}(t)),ne{t}_{i{n}_j(t)}={\sum }_u{w}_{i{n}_j}{y}^u(t-1)$
• 4: $g(ne{t}_{c_j}(t))y^{i{n}_j}(t)$
• 5: $s_{c_j}(t)=s_{c_j}(t-1)+g(ne{t}_{c_j}(t))y^{i{n}_j}(t),s_{c_j}(0)=0$
• 7: $h(s_{c_j}(t))$
• 8: $y^{ou{t}_j}(t)=f(ne{t}_{ou{t}_j}(t)),ne{t}_{ou{t}_j(t)}={\sum }_u{w}_{ou{t}_j}{y}^u(t-1)$
• 9: $y^{c_j}(t)=h(s_{c_j}(t))y^{ou{t}_j}(t)$

上图中并没有展现时序方面的细节，下面我绘制了一个展现时序关系图的记忆细胞（以单个记忆细胞为例）：

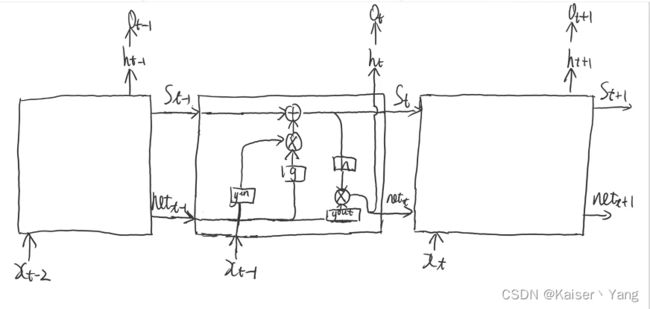
作者简单解释了使用门单元的原因：使用输入门是为了通过权重来控制输入权重冲突，而使用输出门是为了通过权重来控制输出权重冲突（相当于两个作用的一部分被输入门和输出门进行了分担，形成了新的向量代表）。

作者同时指出在某些情况下输出门是可以不需要的（例如Local Output Encoding，但我不太清楚这是一个什么任务），并在Section 5的Experiment 2a和2b做了相关实验。

记忆细胞块（Memory Cell Block）：指的是多个记忆单元串联起来，但是使用同一个的输入门和输出门（如果要展现时序关系的话，则上图每个方块中是多个记忆细胞而不只是一个记忆细胞）

训练过程：使用RTRL进行训练，为了防止梯度消失，当梯度传播到输入门、输出门以及记忆单元的输入时不会再继续传播，在记忆单元之间的反向传播是通过$s$进行的（我理解此时不会再向之前的隐藏层传播），梯度只会在记忆单元之间传播（文章对这里的描述是，当梯度传播到输出门的时候会做一次裁剪，然后在记忆单元中正常传播，到输入门的时候又会做一次裁剪，然后对记忆单元中的权重进行更新，更新完继续反向传播离开记忆单元，此时会再进行一次裁剪，可以参考Figure 2，到达另一个记忆单元（如果存在的话））

计算复杂度：只取决于需要计算导数的参数个数，LSTM的空间复杂度不会随着输入序列的增长而增长，每次的更新复杂度不会随着网络大小的增长而增长。

滥用问题和解决方法（Abuse problem and solutions）：

在训练一开始的时候，即使没有门单元和记忆细胞，损失也会随着训练的进行而下降（此时相当于一个传统的RNN），此时网络就可能会对记忆细胞进行滥用（翻译成错误使用可能更加合理，这里指的是没有正确发挥记忆细胞的功能），仅仅把记忆细胞作为一个偏差（bias）进行使用，也就是此时的记忆细胞的作用可能只是一个可以学习的过滤阀门，这会导致训练难以进行。如果两个记忆细胞保存了相同的信息也可以叫做滥用（此时就是重复使用的意思）。

作者给出了两个解决方法：

• 方法一：在损失不再下降时再加入记忆单元和门单元（实验2采用了这种做法，不采用方法二是因为实验二没有使用输出门）；
• 方法二：输出门一开始加上一个为负的偏差，这样会导致细胞的初始训练时权重偏向于0，等价于在损失不再变化时加上记忆细胞和门（实验1，3，4，5，6采用了这种方法）。

内部状态飘逸和解决方法（Internal state drift and remedies）：如果记忆单元的输入大多数是正（或者大多数为负）内部状态$s_j$会随着时间的推移而出现漂移（漂移是什么文中也没有指出，但是文章指出漂移会让$h^{\prime }$很小从而导致梯度消失，这里我猜测漂移的定义就像训练中出现抖动一样），可以选择合适的$h$来解决这个，而实验中选取的$h(x)=x$并不能满足要求（这个函数没有限制输出的范围）。于是作者采用了一种折中的方法：在训练开始时，给定输入门一个偏向于0的偏差（Section 5的Experiment 4和5采用了这种方法）

5 EXPERIMENTS

现在（2010年之后）的论文十多页可能就结束了，作者的这篇论文长达33页，里面包含了大量的实验和公式推理（相当于理论+自己设计实验进行验证）。

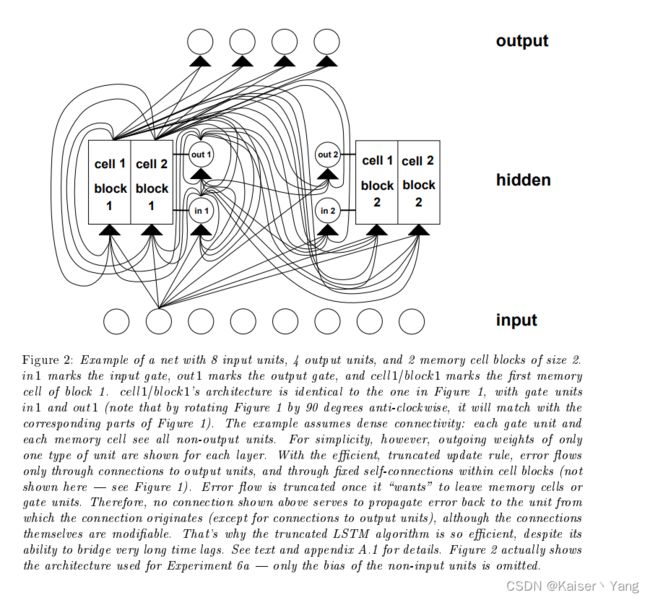
实验整体的模型如Figure 2所示，根据不同的实验调整输入单元个数和输出单元格数以及中间记忆细胞块的大小。

指出之前的模型应用随机的参数对于长时间间隔的任务处理效果甚至好于训练结果。

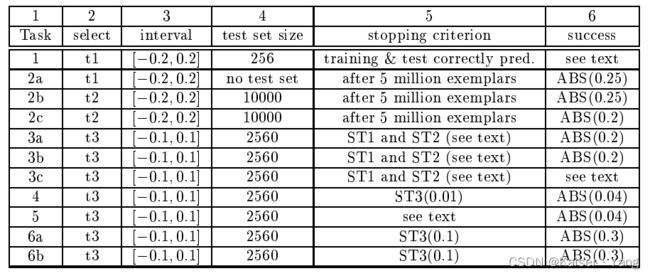
实验的共性：

• 使用在线学习而不吃批量学习；
• 始终使用Sigmoid作为激活函数；
• 实验一和实验二的初始权重范围：$[-0.2,0.2]$，其余实验初始权重范围：$[-0.1,0.1]$；

实验的概述：

• 实验一：基准测试，并不是一个长时间间隔任务，进行该试验有两个原因：（1）实验结果能够展示输出门的好处（2）该实验是RNN非常常用的基准测试。
• 实验二：输入包含很多特征，但是其中重要的特征很少，分为有噪音和无噪音两个版本。
• 实验三：解决长时间间隔问题
• 实验四、五：输入中有用信息相隔较远，需要控制时间间隔的存储精度
• 实验六：包含许多复杂的输入类型（其他模型没有解决这类问题）

5.1 EXPERIMETN 1: EMBEDDED REBER GRAMMAR

任务描述：学习embedded Reber grammar，对于输入的字母预测下一个字母。


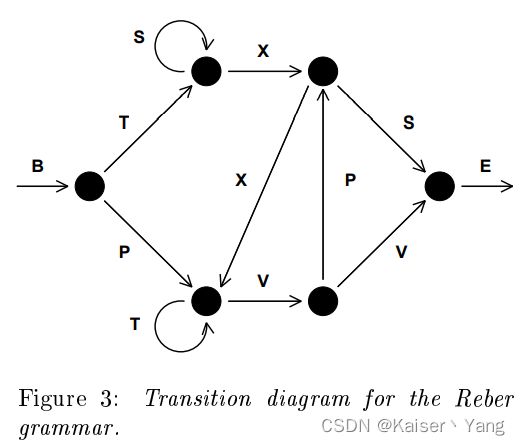
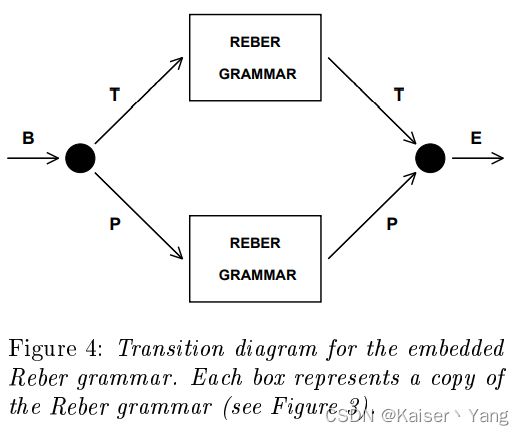
embedded Reber grammar：这是一个产生字符串的方式，产生方法如Figure4和Figure3，B代表Begin，E代表End，从图4的左端进入，在分岔路等概率的选择一个方向，这样可以得到边上的一个字母，一直到E解决即可产生一个字符串，Figure 3是Figure 4中REBER GRAMMAR的结构。

模型：RTLRL，ELM，RCC使用的是之前论文中的模型，这里介绍一下LSTM使用的模型，模型是之前提到的，不同点在于memory block的大小和个数不同，此次实验用了不同大小和个数的memory block，可以从实验结果中看出来。所有的Sigmoid函数的输出是[0,1]，$h$的输出是[-1,1]，$g$的输出是[-2,2]，除了输出门增加了初始化偏差-1，-2，-3，其余的权重初始化为[-0.2,0.2]。

训练数据和测试数据都是随机生成两者不存在交集，如果一次实验的训练集和测试集所有的预测全部正确则认为该次试验成功。

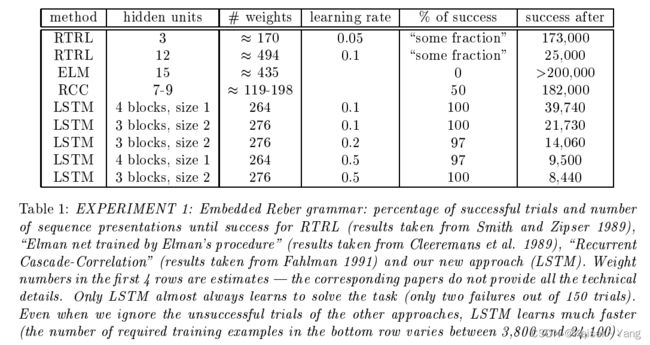
实验结果如Table 1所示（表中还测试了其他模型）。

5.2 EXPERIMENT 2: NOISE-FREE AND NOISY SEQUENCES

5.2.1 Task 2a: noise-free sequences with long time lags

输入有$p+1$个向量每个向量采用独热编码，输入一共有两种形式：$a_{p+1}=y,a_1,a_2,...,a_{p-1},a_{p+1}=y$和$a_p=x,a_1,a_2,...,a_{p-1},a_p=x$这样做是为了验证LSTM的长期记忆能力，为了预测输入序列的最后一个参数，模型必须要记住前$p$个输入才能够成功的预测最后一个参数。

在训练之后，对于10K的连续随机选取的序列，输出的最大的绝对值错误小于0.25则认为此次执行成功。

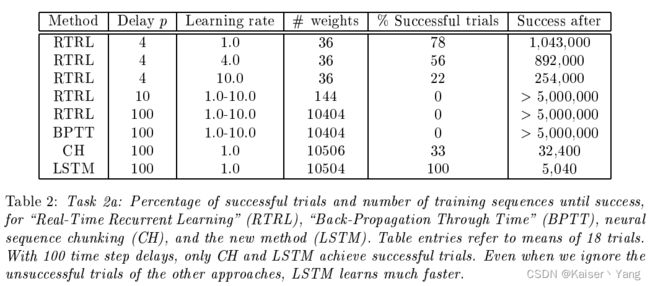
结果如Table 2所示。

5.2.2 Task 2b: no local regularities

对于上一个实验可能中间的输入是固定的，这可能会使得模型对输入进行压缩，于是作者设计了这个实验，将上一个实验中输入的中间部分进行打乱，得到该任务的输入，其余过程与上一个实验相同。

实验结果，其他的模型不能够解决这个任务，而LSTM可以解决这个问题（18次试验的平均结果：在$p=100$的时候，在5680次训练后成功，成功的定义同上）。

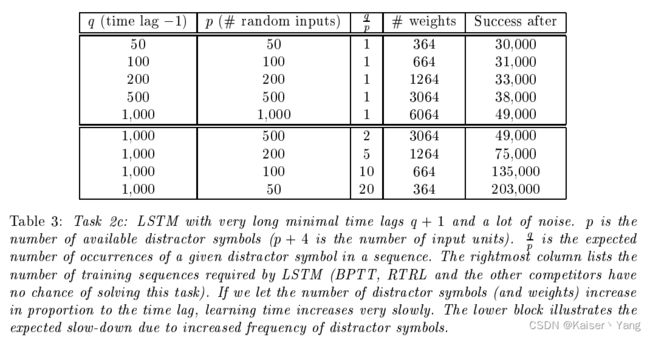
5.2.3 Task 2c: very long time lags – no local regularities

输入的来源：$a_1,...,a_{p-1},a_p,a_{p+1}=e,a_{p+2}=b,a_{p+3}=x,a_{p+4}=y$，每个是一个独热编码的向量

输入的产生，首先输入由多个向量组成，（1）第一个一定是$b$，第二个$x,y$等可能出现，（2）之后会以$\frac{9}{10}$的概率从$a_1,...,a_p$中产生，$\frac{1}{10}$的概率产生$e$，如果不是$e$则继续（2）(最少进行$q$次），如果是则结尾变量与第二个变量相同，也就是说输入的格式如下：$b,x,a,...,a,e,x$或者$b,y,a,...,a,e,y$

可以计算出输入的期望长度为$q+14$（一个简单的等比数列求和）：

$4+{\sum }_{k=0}^{\infty }\frac{1}{10}(\frac{9}{10}{)}^k(q+k)=q+14$

结果如Table 3所示。

5.3 EXPERIMENT 3: NOISE AND SIGNAL ON SAME CHANNEL

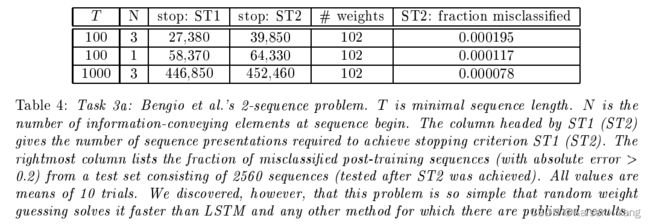
5.3.1 Task 3a

一个二分类问题：输入的前$N$项是有效值，后面部分是高斯分布生成的如果前$N$项等于1那么就是第一类，如果全部等于-1那么就是第二类，序列的总长度在$T$和$T+\frac{1}{10}T$之间，$T$是一个给定值。

训练有两个阶段：

• ST1：256个测试分类全部正确
• ST2：ST1满足的条件下，平均绝对值误差小于0.01（包含额外2560个输入序列）

结果如Table 4所示。

5.3.2 Task 3b

与Task 3a类似，只是在每个输入的前$N$维加上了噪音（均值为0，方差为0.2的高斯分布）

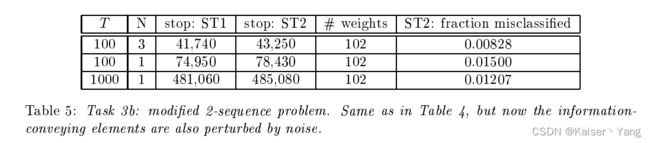
结果如Table 5所示。

5.3.3 Tack 3c

将代表类别1的1换成0.2代表类别2的-1换成0.8同时目标带有噪声（均值0，方差0.1的高斯分布），这样做的目的是为了进一步的增加干扰这样的话随机猜测算法就不能很好的表现了。

停止条件：测试集（包含256组数据）全部分类正确，绝对值误差的均值小于0.015。同时包含2560个其他输入用来查看没有成功匹配的比率。

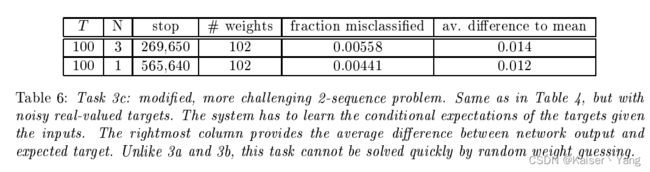
实验结果如Table 6所示。

5.4 EXPERIMENTS 4: ADDING PROBLEM

每个输入是多个组二维向量，每个输入的向量个数在$T$和$T+\frac{1}{10}T$之间，二维向量的第一维是[-1,1]的随机值，第二维是0，1，-1中的一个（确定规则后续会讲）

第二维的$0，1，-1$的确定规则：

• 随机选择前十个中的一个进行标记（设置第二维为1），将这个向量的第一维记为$X_1$
• 接着在前$\frac{T}{2}-1$个向量选择并标记（设置第二维为1）一个没有标记的向量，将这个向量的第一维记为$X_2$（文章这里描述的是前面选择，但是表格给出的最小间隔又是$\frac{T}{2}$我认为这里应该是选择后面的部分才对）
• 将没有标记的所有向量的第二维设置为0
• 将第一个和最后一个向量的第二维设置为-1（极少数情况第一个向量会被标记此时我们把$X_1$设置为0）

正确的输出：$0.5+\frac{X_1+X_2}{4.0}$

内部状态漂移v.s.初始偏差：为了认识到该问题的重要性，作者通过给所有的非输入单元添加偏差让该实验更加复杂（人工促使内部的偏移），按照Section 4中提到的方法：给输入门增加偏差，两个输入门的偏差依次是：$-3.0,-6.0$

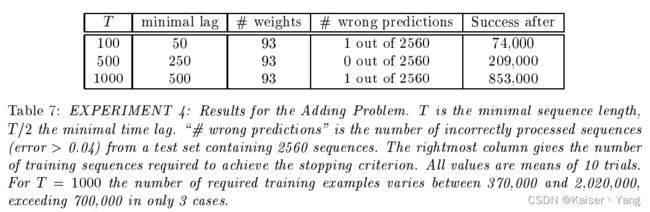
结果如Table 7所示。

5.5 EXPERIMENT 5: MULTIPLICATION PROBLEM

在上一个实验的基础上，将输入向量的第一维的范围控制在$[0,1]$区间上，同时如果出现极少数情况下选中第一个向量的情况，我们把$X_1$设置为1而不是0，正确的输出是变为：$X_1\ast X_2$。

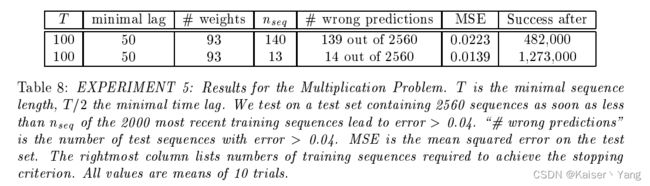
训练结果如Table 8所示

5.6 EXPERIMENT 6: TEMPORAL ORDER

5.6.1 Task 6a: two relevant, widely separated symbols

是一个四分类问题，输入的长度在100和110之间，输入开始与E结束于B，中间的部分是从$a,b,c,d$随机选取，除此之外随机选择$t_1(10\le t_1\le 20)$和$t_2(50\le t_2\le 60)$处更改为$X或Y$此时就产生了四类型的序列：

• $Q$：代表选择的两个位置都是$X$
• $R$：代表选择的第一个位置是$X$第二个是$Y$
• $S$：代表选择的第一个位置是$Y$第二个是$X$
• $Y$：代表选择的两个位置都是$Y$

输入中的字母采用独热编码表示

5.6.2 Task 6b: three relevant, widely separated symbols

与上一个问题类似只是需要选择三个$t_1(10\le t_1\le 20),t_2(66\le t_2\le 76),t_3(66\le t_3\le 76)$，根据位置的不同选择分为八类：

• $X,X,X->Q$
• $X,X,Y->R$
• $X,Y,X->S$
• $X,Y,Y->U$
• $Y,X,X->V$
• $Y,X,Y->A$
• $Y,Y,X->B$
• $Y,Y,Y->C$
  
  两次测试结果如Table 9所示。

5.7 SUMMARY OF EXPERIMENTAL CONDITIONS

这一部分只是给出了上述所有实验的更加详细的参数：

6 DISCUSSION

LSTM的限制：

• 很难处理类似于“长时间间隔的异或问题”（数据带有噪声会更加难处理）原因在于问题不能够被分解成一个简单的子问题。该类问题理论上可以增加MLP来解决，但是复杂度会增加，但作者没有做过相关的实验。
• 每个记忆单元会比传统的RNN多一些参数
• LSTM的问题与一次性读取整个输入的MLP的问题类似

LSTM的好处：

• LSTM的常数反向传播使得其能够很好的处理长时间间隔问题
• LSTM能够处理带噪音的部分问题
• 即使关键输入高度分散，LSTM也能够胜任
• 可以不用做微调（学习率，输入门偏差，输出门偏差）
• 每个时间步的每个权重的更新时$O(1)$的

7 CONCLUSION

保证常数的梯度，门单元能够控制梯度时候反向传播。

未来的应用：时间序列预测，音乐编曲，演讲处理

APPENDIX

附录包含了所有公式的推导，以及LSTM的反向传播，LSTM的反向传播推导比较繁琐，这里就不给出附录的说明，简单的说明为什么LSTM不会出现RNN的梯度消失的问题：

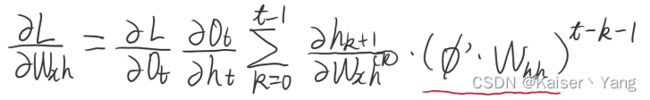
我们先来看equation (2)作者提出了NAIVE APPROACH就是让图中红色划线部分等于1，而LSTM和这个有着异曲同工之妙，在加入了输入门和输出门之后，反向传播的路径变的非常复杂（每一时刻反向传播路径增加$m$条，根据乘法原理向前$k$步就会增加$m^k$条）在进行求导的过程中有的路径中的梯度还是会出现梯度消失的问题，但是由于有了输入门和输出门的权重控制，可以让模型学习参数来使得在反向传播的时候大多数路径中的乘数是$1$保存了大多数梯度，这也使得LSTM能够处理长时间间隔问题。