【原理+源码详细解读】从Transformer到ViT
文章目录
-
- 参考文献
- 简介
- Transformer架构
-
- Position Encoding
- Self-attention
- Multi-head Self-attention
- Masked Multi-Head Self-attention
- Layer Normalization
- Feed Forward Network
- Encoder Layer
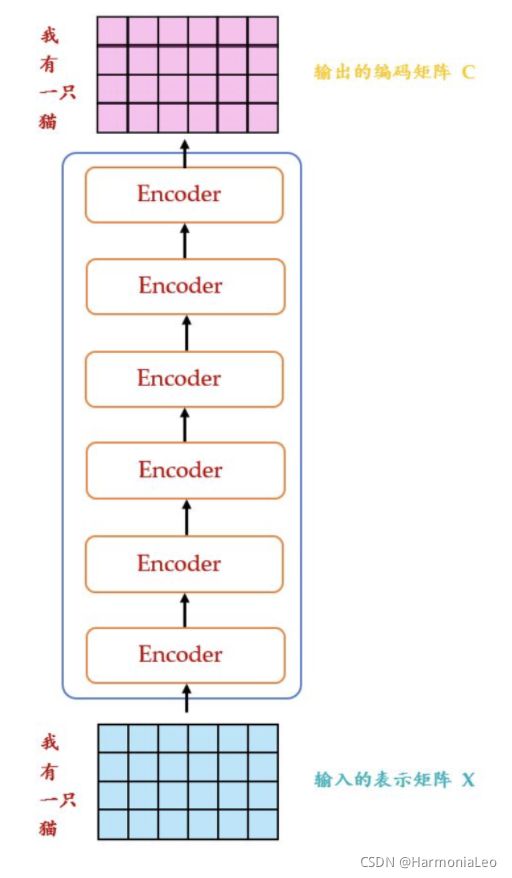
- Encoder
- Decoder Layer
- Decoder
- 总体流程
- ViT流程
-
- 图片分块
- Patch Embedding
- Class Token
- Position Encoding
- Transformer
- Predition Head
- 整体流程
- 训练方法
- 实验
-
- 性能对比
- ViT对预训练数据的要求
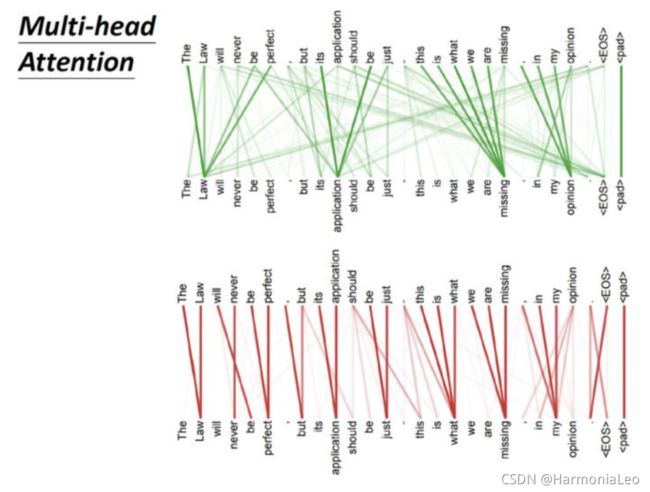
- ViT的注意力机制
- Transformer源码阅读注释
- ViT源码阅读注释
参考文献
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale: https://arxiv.org/abs/2010.11929(发布于ICLR2021)
Attention Is All You Need: https://arxiv.org/abs/1706.03762
ViT: 简简单单训练一个Transformer Encoder做个图像分类:https://zhuanlan.zhihu.com/p/370979971
Vision Transformer 超详细解读 (原理分析+代码解读) (一):https://zhuanlan.zhihu.com/p/340149804
Vision Transformer 超详细解读 (原理分析+代码解读) (二):https://zhuanlan.zhihu.com/p/342261872
简介
Transformer 是 Google 的团队在 2017 年提出的一种 NLP 经典模型,使用了 Self-Attention 机制,不采用 RNN 的顺序结构,使得模型可以并行化训练,而且能够拥有全局信息。
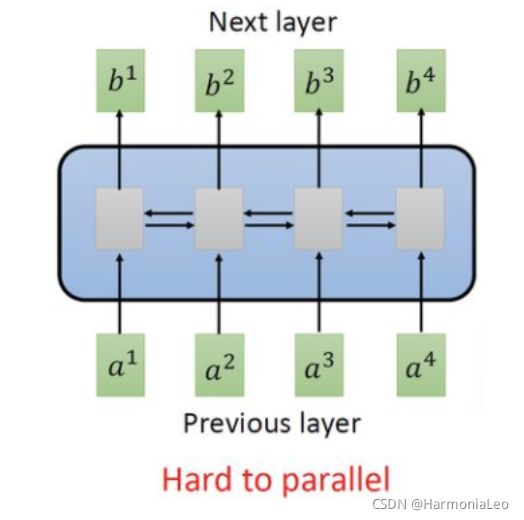
RNN可以以序列的全局信息作为输入来进行工作,但很不容易并行化,因为RNN是有记忆的,后面的计算需要依靠前面计算的结果。
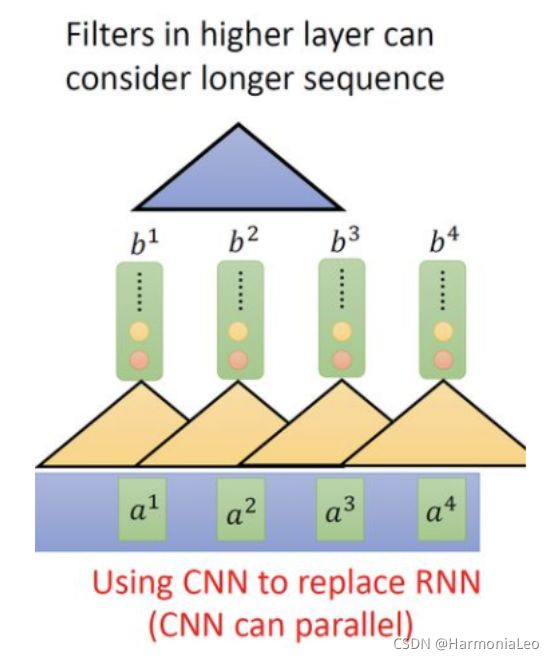
因此有人提出把CNN拿来取代RNN。卷积操作是可以并行实现的,但只能考虑非常有限的内容,即一个卷积核范围内的数据。不过,通过堆叠卷积层,上层的卷积核内就可以考虑时间或空间距离上较远的数据之间的关系。但就算如此,需要堆叠许多层卷积层这一问题,往往会使得CNN网络的结构变得异常复杂和庞大。
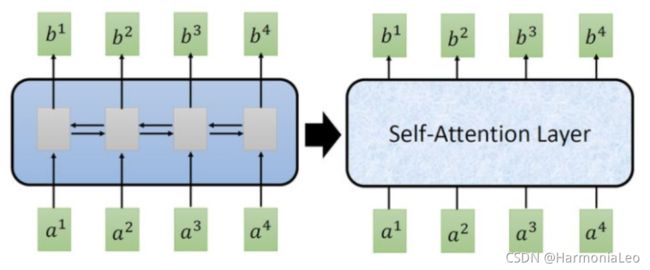
而今天有一个新的想法,那就是用自注意层取代RNN所做的事情。它的输入和输出和RNN是一模一样的,输入一个序列,输出一个序列,可以考虑时间和空间上距离较远的数据之间的关系,而又可以进行并行化计算。
而ViT则本着尽可能少修改的原则,将原版的Transformer开箱即用地迁移到图像分类任务上面。作者认为,没有必要总是依赖于CNN,只用Transformer也能够在图像分类任务中表现很好,尤其是在使用大规模训练集的时候。同时,在大规模数据集上预训练好的模型,在迁移到中等数据集或小数据集的分类任务上以后,也能取得比CNN更优的性能。
实际上,网上的解读文章,包括论文本身,对于Transformer和ViT架构的阐述都有许多省略和模糊的地方。本文在对Transformer和ViT的源码进行仔细研读后,给出了对Transformer和ViT架构所有细节的完整呈现,并在本文最后给出了Transformer和ViT的源码与自己写的注释。
Transformer架构
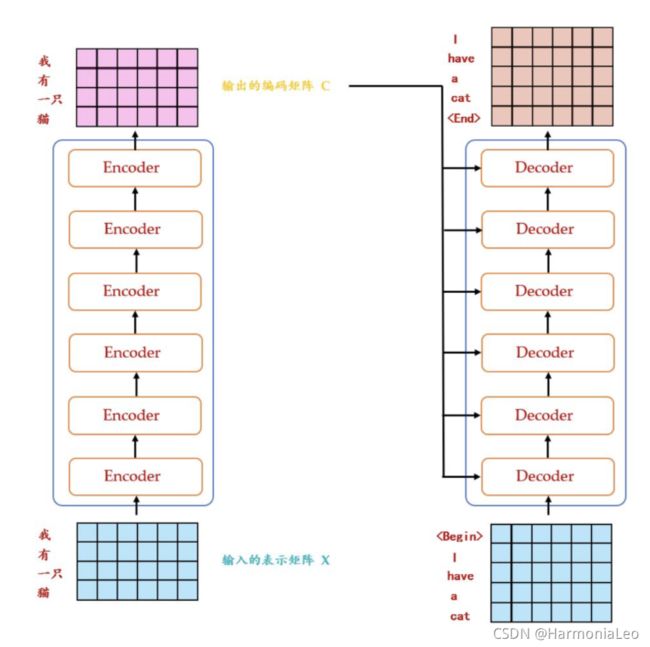
我们以机器翻译任务为例来对Transformer架构进行介绍
Position Encoding
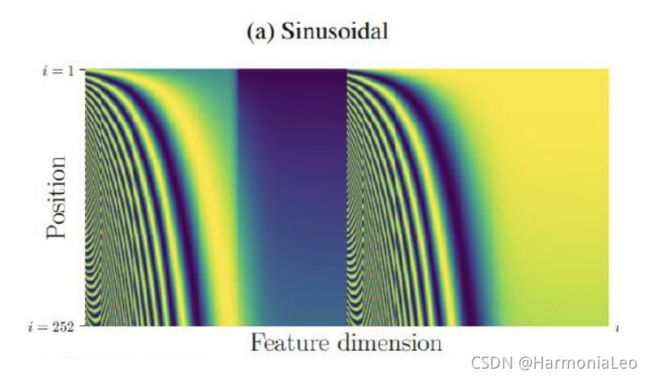
设有输入数据 X X X( N × d N\times d N×d)(每行一条数据),对于位于pos位置的数据(输入 X X X的每一行),有长为d的行向量 P E p o s ⃗ \vec{PE_{pos}} PEpos,其第i位满足 { P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i d ) P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i + 1 d ) ( i ∈ 0 , 1... , d 2 − 1 ) \begin{cases}PE(pos,2i)=sin(\frac{pos}{10000^{\frac{2i}{d}}})\\PE(pos,2i+1)=cos(\frac{pos}{10000^{\frac{2i+1}{d}}})\end{cases}(i\in0,1...,\frac{d}{2}-1) ⎩⎨⎧PE(pos,2i)=sin(10000d2ipos)PE(pos,2i+1)=cos(10000d2i+1pos)(i∈0,1...,2d−1),将每一行的 P E p o s ⃗ \vec{PE_{pos}} PEpos加到输入数据的对应行上得到 X ^ \hat X X^
pos位置在分配时,给定一个最大的pos值 p o s m a x pos_{max} posmax(默认200),然后第j行有 p o s = j N p o s m a x pos=\frac{j}{N}pos_{max} pos=Njposmax
Self-attention
比起RNN更加具有并行化能力,比起CNN能建立与时间上相隔更远的数据的联系
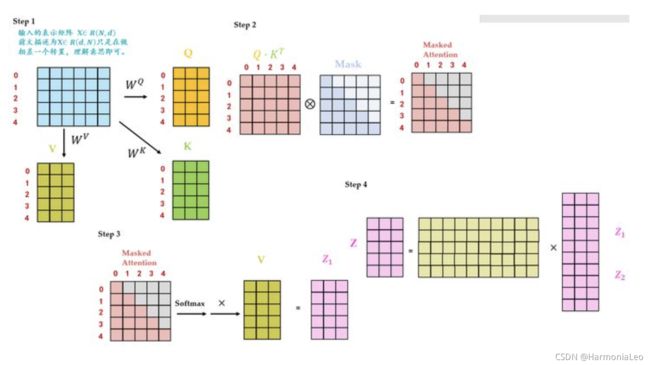
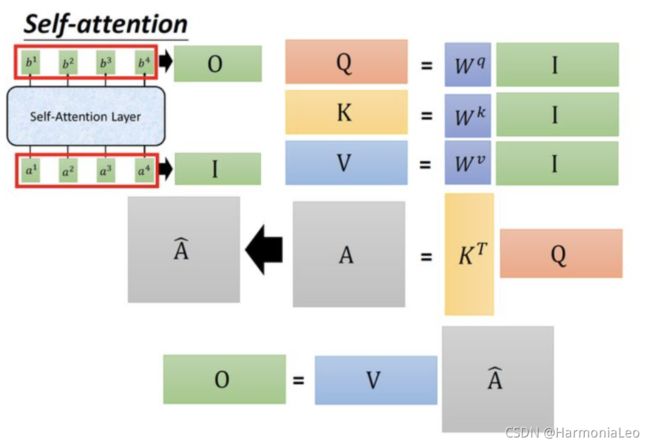
- 设有输入数据 X ^ \hat X X^( N × d N\times d N×d)(每列一条数据),有三个不同的变换矩阵 W q W_q Wq( d × d 1 d\times d_1 d×d1)、 W k W_k Wk( d × d 1 d\times d_1 d×d1)、 W v W_v Wv( d × d 2 d\times d_2 d×d2),变换得到三个矩阵 Q = X W q Q=XW_q Q=XWq($ N\times d_1 ) 、 )、 )、K=XW_k ( ( ( N\times d_1 ) 、 )、 )、V=XW_v ( ( ( N\times d_2$)
- 将 Q Q Q中每个向量和 K K K中每个向量计算内积(自注意过程,匹配两个向量有多接近),并进行归一化(因为内积的数值会随着d的增大而增大): A = Q K T d A=\frac{QK^T}{\sqrt{d}} A=dQKT( N × N N\times N N×N)
- 每行进行softmax操作: A i , j ^ = e A i , j ∑ k e A i , k \hat{A_{i,j}}=\frac{e^{A_{i,j}}}{\displaystyle\sum_{k}e^{A_{i,k}}} Ai,j^=k∑eAi,keAi,j
- 乘以 V V V矩阵得到 O = A ^ V O=\hat AV O=A^V( N × d 2 N\times d_2 N×d2)
- 使用一个线性层 W O W^O WO( d 2 × d d_2\times d d2×d)改变维度: O = W O O ^ O=W^O\hat O O=WOO^( N × d N\times d N×d)
- 通过一个dropout层
Multi-head Self-attention
-
使用 h h h组自注意机制来提取多个输出矩阵 O m O_m Om($ N\times d_2$)
-
多个输出矩阵按行拼接,得到 O ^ \hat O O^( N × ( d 2 × h ) N\times (d_2\times h) N×(d2×h))
-
使用一个线性层 W O W^O WO( ( d 2 × h ) × d (d_2\times h)\times d (d2×h)×d)改变维度: O = W O O ^ O=W^O\hat O O=WOO^( N × d N\times d N×d)
不同的自注意头会注意不同规模的数据
Masked Multi-Head Self-attention
在self-attention的2和3步之间,将 A A A逐点乘上一个下三角矩阵,表示只考虑某一行及其之前行的数据,这是为了保证输入数据的因果性
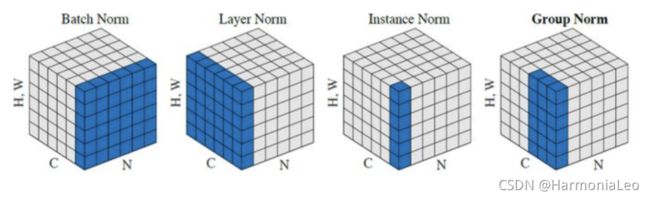
Layer Normalization
Layer Normalization在一个batch中每个 X X X内部进行均值方差归一化
Feed Forward Network
前馈神经网络,包含一个输入层,一个隐藏层+relu函数,一个输出层,在输出层进行dropout
指定隐藏层的神经元个数为 d h d_h dh,则输入层到隐藏层的权重矩阵尺寸为 d × d h d\times d_h d×dh,隐藏层到输出层的权重矩阵尺寸为 d h × d d_h\times d dh×d
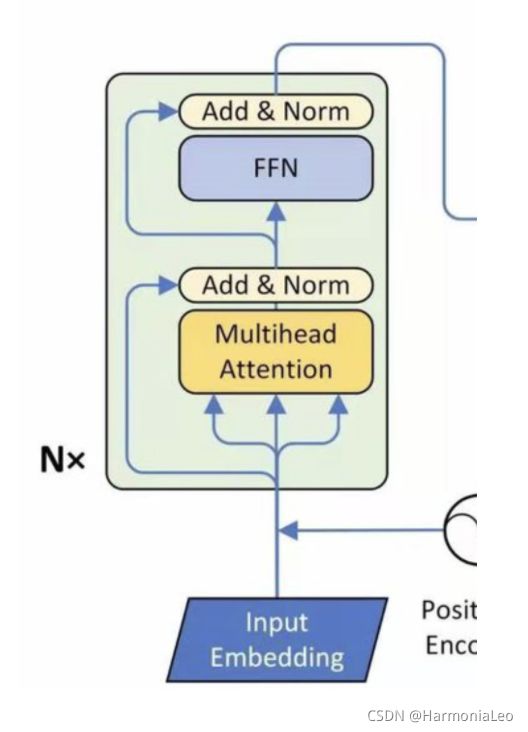
Encoder Layer
- 输入数据 X X X ( N × d ) (N\times d) (N×d),通过一个Multi-head Self-attention层,输出形状也为 ( N × d ) (N\times d) (N×d)
- 残差连接,将输入数据和输出直接相加
- 进行一次Layer Normalization
- 通过一个Feed Forward Network
- 残差连接,将输入数据和输出直接相加
- 进行一次Layer Normalization
Encoder
- 将源语言字符串嵌入为词向量矩阵 N × d N\times d N×d
- 附加位置编码
- 通过一个dropout层
- 进行一次Layer Normalization
- 通过多个堆叠的Encoder Layer,输出结果
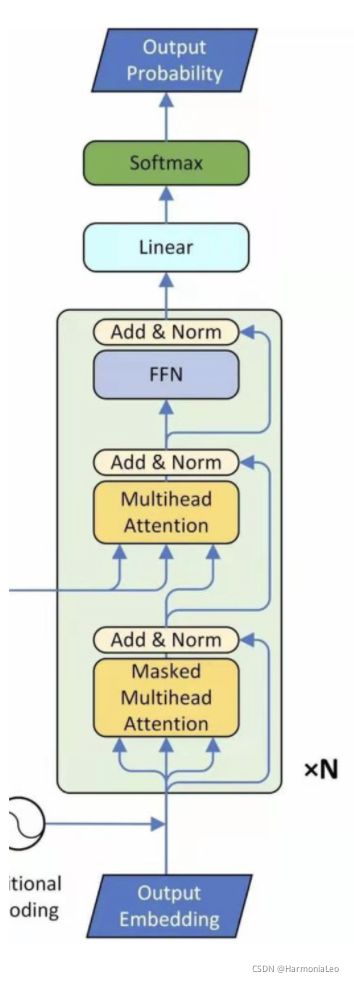
Decoder Layer
- 输入数据 X X X ( N × d ) (N\times d) (N×d),通过一个Masked Multi-head Self-attention层,输出形状也为 ( N × d ) (N\times d) (N×d)
- 残差连接,将输入数据和输出直接相加
- 进行一次Layer Normalization
- 将Encoder的输出和上一步的输出通过一个Multi-head Self-attention层(计算Q时使用上一步的输出,计算K、V时使用Encoder的输出),输出形状也为 ( N × d ) (N\times d) (N×d)
- 残差连接,将输入数据和输出直接相加
- 进行一次Layer Normalization
- 通过一个Feed Forward Network
- 残差连接,将输入数据和输出直接相加
- 进行一次Layer Normalization
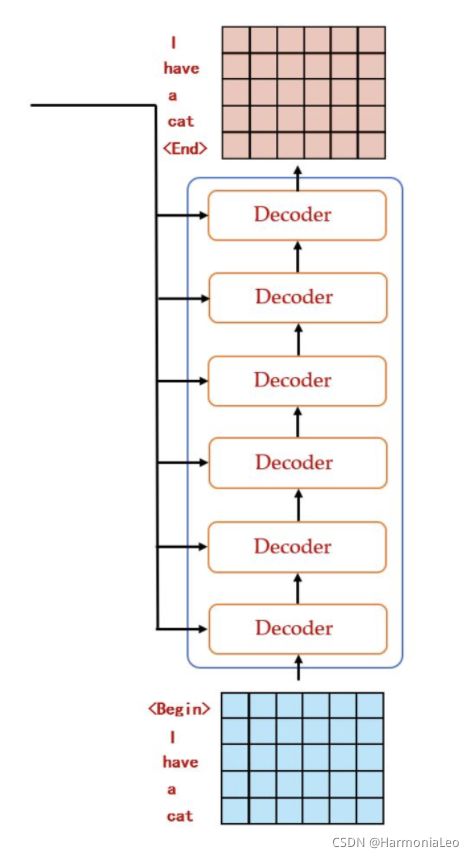
Decoder
- 将目标语言字符串嵌入为词向量矩阵 N × d N\times d N×d
- 附加位置编码
- 通过一个dropout层
- 进行一次Layer Normalization
- 通过多个堆叠的Decoder Layer,输出结果
总体流程
ViT流程
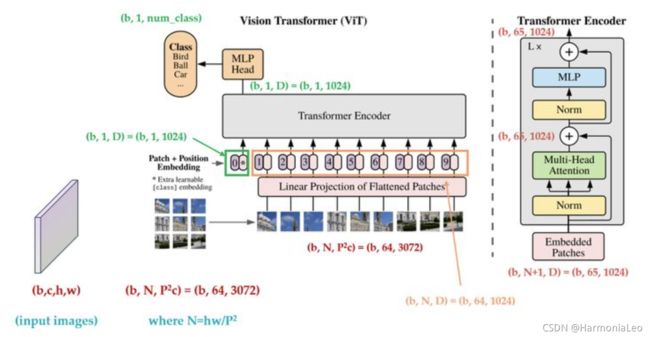
图片分块
首先把 x ∈ H × W × C x\in H\times W\times C x∈H×W×C的图像,变成一个 x p ∈ N × ( P 2 ⋅ C ) x_p\in N\times(P^2·C) xp∈N×(P2⋅C)的sequence of flattened 2D patches。这个序列中一共有 N = H W P 2 N=\frac{HW}{P^2} N=P2HW个展平的2D块,每个块是一个长度为 ( P 2 ⋅ C ) (P^2·C) (P2⋅C)的图片编码行向量
Patch Embedding
对每个图片编码行向量乘以 ( P 2 ⋅ C ) × d (P^2·C)\times d (P2⋅C)×d的矩阵 E E E进行线性变换,将每个行向量长度变为 d d d
Class Token
在图片编码向量矩阵的第一行新增一个随机初始化的长度为 d d d的向量,这样图片编码向量矩阵的尺寸就会变为 ( N + 1 ) × d (N+1)\times d (N+1)×d
这个向量在通过Transformer后,会被用于分类。之所以可以用这个向量来分类,是因为在自注意机制中,每个向量都和其他向量进行了自注意,因此每个向量在通过Transformer后都包含了全局的信息
网络同时也可以设置使用一张图片中所有编码行向量的均值向量来进行分类
Position Encoding
ViT中不再使用原版Transformer的Position Encoding方法,而是让每个图片编码向量都加上一个随机初始化的向量,希望能够通过训练的方式来训练Position Encoding信息
Transformer
ViT中使用的Transformer只包括了Encoder的部分,Encoder的输出( N × d N\times d N×d)就被直接拿去做分类任务了
比较不同的是Feed Forward Network的架构:
- 原版Transformer的FFN包含一个输入层,一个隐藏层+relu函数,一个输出层,再通过一个dropout层,指定隐藏层的神经元个数为 d h d_h dh,则输入层到隐藏层的权重矩阵尺寸为 d × d h d\times d_h d×dh,隐藏层到输出层的权重矩阵尺寸为 d h × d d_h\times d dh×d
- ViT的FFN使用的是GELU激活函数,并且在通过GELU函数后、通过输出层之前,还有一个dropout层
Predition Head
包括一个Layer Norm和一个全连接网络,权值矩阵的尺寸为 d × c l a s s n u m d\times classnum d×classnum, c l a s s n u m classnum classnum为类别数
整体流程
- 图片分块
- Patch Embedding
- 连接上Class Token向量
- 加上Position Encoding
- 通过一个dropout层
- 通过Transformer
- Class Token向量(或者所有编码行向量的均值向量)通过Predition Head,输出每一类的概率
训练方法
先在大数据集上预训练,再迁移到小数据集上面。预训练模型使用到的数据集有:
- ILSVRC-2012 ImageNet dataset:1000 classes
- ImageNet-21k:21k classes
- JFT:18k High Resolution Images
将预训练迁移到的数据集有:
- CIFAR-10/100
- Oxford-IIIT Pets
- Oxford Flowers-102
- VTAB
作者设计了3种不同大小的ViT模型来进行实验:
| DModel | Layers(编解码层数) | Hidden size(自注意过程中矩阵乘法输出向量大小) | MLP size(FFN中隐藏层大小) | Heads(注意力头数) | Params |
|---|---|---|---|---|---|
| ViT-Base | 12 | 768 | 3072 | 12 | 86M |
| ViT-Large | 24 | 1024 | 4096 | 16 | 307M |
| ViT-Huge | 32 | 1280 | 5120 | 16 | 632M |
实验使用准确率作为评价指标。
实验
性能对比
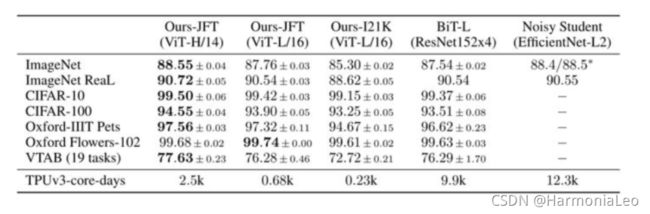
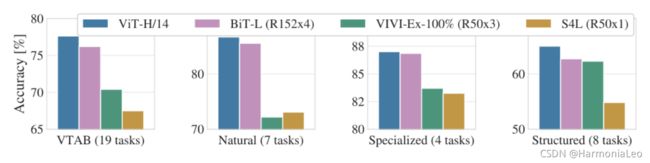
经过大数据集的预训练后,对比当前一些主流CNN,性能达到了SOTA。
VTAB数据集在Natural, Specialized, 和Structured子任务与CNN模型相比的性能上,ViT模型仍然可以取得最优。
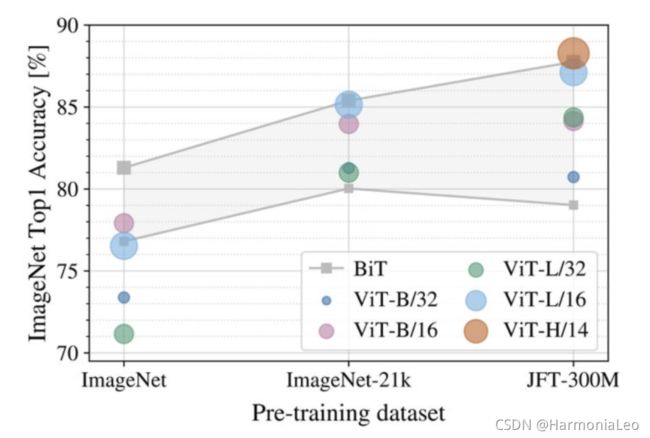
ViT对预训练数据的要求
分别在下面这几个数据集上进行预训练:ImageNet, ImageNet-21k, 和JFT-300M。
当在最小数据集ImageNet上进行预训练时,尽管进行了大量的正则化等操作,但ViT-H模型的性能不如ViT-B模型。使用稍大的ImageNet-21k预训练,它们的表现也差不多。只有使用JFT 300M,我们才能看到更大的ViT模型全部优势。图3还显示了不同大小的BiT模型跨越的性能区域。BiT CNNs在ImageNet上的表现优于ViT,但在更大的数据集上,ViT超过了所有的模型,取得了SOTA。
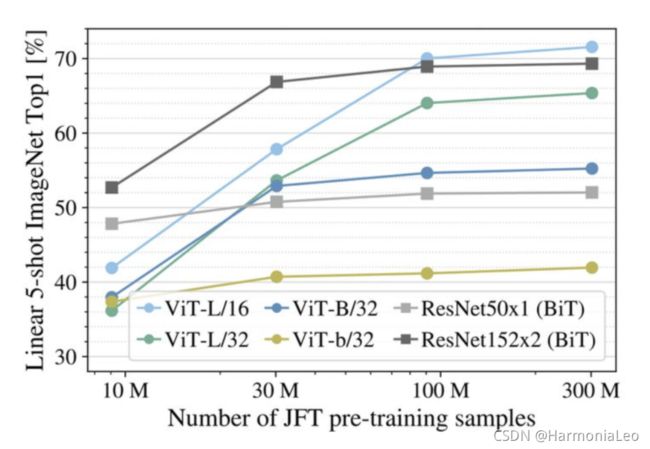
在9M、30M和90M的随机子集以及完整的JFT300M数据集上训练模型,结果如下图所示。 ViT在较小数据集上的计算成本比ResNet高, ViT-B/32比ResNet50稍快;它在9M子集上表现更差, 但在90M+子集上表现更好。ResNet152x2和ViT-L/16也是如此。这说明残差对于较小的数据集是有用的,但是对于较大的数据集,像注意力一样学习相关性就足够了,甚至是更好的选择。
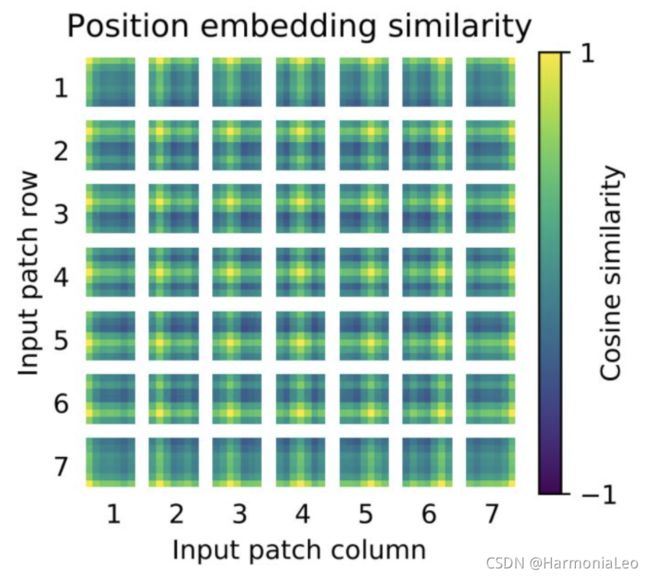
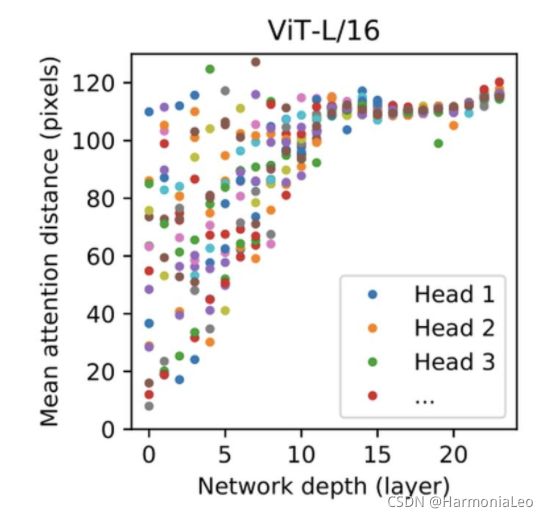
ViT的注意力机制
根据注意力权重计算图像空间中整合信息的平均距离。
在最底层,有些自注意头也已经注意到了图像的大部分,说明这些自注意头负责了全局信息的整合,而其他的头只注意到了图像的一小部分,说明它们负责本地信息的整合。注意力距离随深度的增加而增加,说明随着网络深度增加,注意力将会越发接近于全局。
Transformer源码阅读注释
class ScaledDotProductAttention(nn.Module):
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3)) #Q*KT/归一化因子
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9) #进行mask操作
attn = self.dropout(F.softmax(attn, dim=-1)) #softmax层,加上一个dropout
output = torch.matmul(attn, v) #再乘上V
return output, attn
class PositionalEncoding(nn.Module):
def __init__(self, d_hid, n_position=200): #d_hid为词向量维数
super(PositionalEncoding, self).__init__()
self.register_buffer('pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))
def _get_sinusoid_encoding_table(self, n_position, d_hid):
def get_position_angle_vec(position): #计算编码数值
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) #每个2i位
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) #每个2i+1位
return torch.FloatTensor(sinusoid_table).unsqueeze(0) #(1,N,d)
def forward(self, x):
return x + self.pos_table[:, :x.size(1)].clone().detach() #编码向量是不求导的
class MultiHeadAttention(nn.Module):
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False) #W_q,多个自注意头结果沿行拼接
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False) #W_k,多个自注意头结果沿行拼接
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False) #W_v,多个自注意头结果沿行拼接
self.fc = nn.Linear(n_head * d_v, d_model, bias=False) #降维用线性层
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5) #计算自注意,temperature是归一化因子
self.dropout = nn.Dropout(dropout) #dropout
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) #layernorm
def forward(self, q, k, v, mask=None):
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)
residual = q
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
#计算出三个矩阵。这里有个拆分操作,在生成q、k、v时多个自注意头生成的结果是沿行拼接的,这里将每个自注意头的结果拆分到了一个新的维度上
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2) #调换“第几个词向量”这个维度和“第几个自注意头”这个维度
if mask is not None:
mask = mask.unsqueeze(1) #对mask升维,以便之后与4维张量进行mask操作
q, attn = self.attention(q, k, v, mask=mask) #矩阵相乘,计算自注意
#q (sz_b,n_head,N=len_q,d_k)
#k (sz_b,n_head,N=len_k,d_k)
#v (sz_b,n_head,N=len_v,d_v)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1) #变回沿行拼接
#q (sz_b,len_q,n_head*d_k)
q = self.dropout(self.fc(q)) #降为正常维数,并dropout
q += residual #残差连接
q = self.layer_norm(q) #layer_norm
return q, attn
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_in, d_hid, dropout=0.1):
super().__init__()
self.w_1 = nn.Linear(d_in, d_hid)
self.w_2 = nn.Linear(d_hid, d_in)
self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
residual = x
x = self.w_2(F.relu(self.w_1(x))) #隐藏层
x = self.dropout(x) #dropout
x += residual #残差连接
x = self.layer_norm(x) #layernorm
return x
class EncoderLayer(nn.Module):
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(EncoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
#每个编码层包括一个自注意层和一个FFN
def forward(self, enc_input, slf_attn_mask=None):
enc_output, enc_slf_attn = self.slf_attn(enc_input, enc_input, enc_input,mask=slf_attn_mask) #编码层中,计算Q、K、V都使用源语言词向量矩阵(第一层编码层)、或者上一层编码层的输出(非第一层编码层)
enc_output = self.pos_ffn(enc_output) #FFN
return enc_output, enc_slf_attn
class DecoderLayer(nn.Module):
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(DecoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.enc_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
#每个解码器包括一个自注意层、一个编解码注意层和一个FFN
def forward(self, dec_input, enc_output,slf_attn_mask=None, dec_enc_attn_mask=None):
dec_output, dec_slf_attn = self.slf_attn(dec_input, dec_input, dec_input,mask=slf_attn_mask) #解码层中,自注意层计算Q、K、V都使用目标语言词向量矩阵(第一层解码层)、或者上一层解码层的输出(非第一层解码层)
dec_output, dec_enc_attn = self.enc_attn(dec_output, enc_output, enc_output, mask=dec_enc_attn_mask) #编解码注意层计算Q时使用目标语言词向量矩阵(第一层解码层)、或者上一层解码层的输出(非第一层解码层),计算K、V时使用编码器的输出
dec_output = self.pos_ffn(dec_output) #FFN
return dec_output, dec_slf_attn, dec_enc_attn
class Encoder(nn.Module):
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200):
super().__init__()
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx) #嵌入层定义,将源语言的字符串数组中每个字符串嵌入为词向量矩阵
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position) #附加上位置编码
self.dropout = nn.Dropout(p=dropout)
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)]) #堆叠编码层
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) #layernorm层
def forward(self, src_seq, src_mask, return_attns=False):
enc_slf_attn_list = []
enc_output = self.dropout(self.position_enc(self.src_word_emb(src_seq))) #嵌入、附加位置编码、dropout
enc_output = self.layer_norm(enc_output) #layernorm
for enc_layer in self.layer_stack:
enc_output, enc_slf_attn = enc_layer(enc_output, slf_attn_mask=src_mask) #输入是源语言词向量矩阵,进行掩码,并通过每一层编码层
enc_slf_attn_list += [enc_slf_attn] if return_attns else []
if return_attns:
return enc_output, enc_slf_attn_list
return enc_output, #输出编码结果
class Decoder(nn.Module):
def __init__(
self, n_trg_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, n_position=200, dropout=0.1, scale_emb=False):
super().__init__()
self.trg_word_emb = nn.Embedding(n_trg_vocab, d_word_vec, padding_idx=pad_idx) #嵌入层定义,将目标语言的字符串数组中每个字符串嵌入为词向量矩阵
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position) #附加上位置编码
self.dropout = nn.Dropout(p=dropout)
self.layer_stack = nn.ModuleList([
DecoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)]) #堆叠解码层
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) #layernorm
self.scale_emb = scale_emb
self.d_model = d_model
def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):
dec_slf_attn_list, dec_enc_attn_list = [], []
dec_output = self.dropout(self.position_enc(self.trg_word_emb(trg_seq))) #嵌入、附加位置编码、dropout
dec_output = self.layer_norm(dec_output) #layernorm
for dec_layer in self.layer_stack:
dec_output, dec_slf_attn, dec_enc_attn = dec_layer(dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask) #输入是目标语言词向量矩阵以及编码器的输出,进行掩码,并通过每一层解码层
dec_slf_attn_list += [dec_slf_attn] if return_attns else []
dec_enc_attn_list += [dec_enc_attn] if return_attns else []
if return_attns:
return dec_output, dec_slf_attn_list, dec_enc_attn_list
return dec_output, #输出解码结果
def get_pad_mask(seq, pad_idx):
return (seq != pad_idx).unsqueeze(-2)
def get_subsequent_mask(seq):
sz_b, len_s = seq.size()
subsequent_mask = (1 - torch.triu(torch.ones((1, len_s, len_s), device=seq.device), diagonal=1)).bool() #首先定义一个全1矩阵,然后返回上三角部分,再用1减去该矩阵得到下三角部分。diagonal=1表示只包含对角线以上1位的部分
return subsequent_mask
class Transformer(nn.Module):
def __init__(
self, n_src_vocab, n_trg_vocab, src_pad_idx, trg_pad_idx,
d_word_vec=512, d_model=512, d_inner=2048,
n_layers=6, n_head=8, d_k=64, d_v=64, dropout=0.1, n_position=200,
trg_emb_prj_weight_sharing=True, emb_src_trg_weight_sharing=True):
#n_src_vocab是源语言的字典大小
#n_trg_vocab是目标语言的字典大小
#src_pad_idx是源语言的字符串列表中每一句在嵌入为词向量矩阵时,词向量数目不相等时用于补位的数字
#trg_pad_idx是目标语言的字符串列表中每一句在嵌入为词向量矩阵时,词向量数目不相等时用于补位的数字
#d_word_vec是嵌入层输出词向量维数
#d_model是输入模型的词向量维数
#d_inner是FFN中隐藏层维数
#n_layers为编码器和解码器的层数
#n_head表示注意力头数
#d_k为W_k和W_q矩阵的输出维数
#d_v为W_v矩阵的输出维数
#dropout为网络中所有dropout层的dropout率
super().__init__()
self.src_pad_idx, self.trg_pad_idx = src_pad_idx, trg_pad_idx
self.encoder = Encoder(
n_src_vocab=n_src_vocab, n_position=n_position,
d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
pad_idx=src_pad_idx, dropout=dropout)
self.decoder = Decoder(
n_trg_vocab=n_trg_vocab, n_position=n_position,
d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
pad_idx=trg_pad_idx, dropout=dropout)
self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False) #输出层,从模型输出映射到目标语言的字典
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p) #所用向量使用xavfier初始化
assert d_model == d_word_vec #是嵌入层输出词向量维数和输入模型的词向量维数需要一致
self.x_logit_scale = 1.
if trg_emb_prj_weight_sharing:
self.trg_word_prj.weight = self.decoder.trg_word_emb.weight
self.x_logit_scale = (d_model ** -0.5)
if emb_src_trg_weight_sharing:
self.encoder.src_word_emb.weight = self.decoder.trg_word_emb.weight
def forward(self, src_seq, trg_seq):
src_mask = get_pad_mask(src_seq, self.src_pad_idx) #编码器输入不需要屏蔽未来信息
trg_mask = get_pad_mask(trg_seq, self.trg_pad_idx) & get_subsequent_mask(trg_seq) #解码器输入需要屏蔽未来信息
enc_output, *_ = self.encoder(src_seq, src_mask) #编码过程
dec_output, *_ = self.decoder(trg_seq, trg_mask, enc_output, src_mask) #解码过程
seq_logit = self.trg_word_prj(dec_output) * self.x_logit_scale #输出映射
return seq_logit.view(-1, seq_logit.size(2))
ViT源码阅读注释
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) + x #残差连接
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs) #layernorm
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout = 0.):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim), #第一层线性层
nn.GELU(), #GELU
nn.Dropout(dropout), #dropout
nn.Linear(hidden_dim, dim), #第二层线性层
nn.Dropout(dropout) #dropout
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
super().__init__()
inner_dim = dim_head * heads #多个自注意头结果沿行拼接
self.heads = heads
self.scale = dim ** -0.5 #归一化因子
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False) #W_q、W_k、W_v三个矩阵沿行拼接,一次生成QKV
self.to_out = nn.Sequential(nn.Linear(inner_dim, dim),nn.Dropout(dropout))
def forward(self, x, mask = None):
b, n, _, h = *x.shape, self.heads
# self.to_qkv(x): b, 65, 64*8*3
# qkv: b, 65, 64*8
qkv = self.to_qkv(x).chunk(3, dim = -1)
# b, 65, 64, 8
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = h), qkv)
# dots:b, 65, 64, 64
dots = torch.einsum('bhid,bhjd->bhij', q, k) * self.scale
mask_value = -torch.finfo(dots.dtype).max
if mask is not None:
mask = F.pad(mask.flatten(1), (1, 0), value = True)
assert mask.shape[-1] == dots.shape[-1], 'mask has incorrect dimensions'
mask = mask[:, None, :] * mask[:, :, None]
dots.masked_fill_(~mask, mask_value)
del mask
# attn:b, 65, 64, 64
attn = dots.softmax(dim=-1)
# 使用einsum表示矩阵乘法:
# out:b, 65, 64, 8
out = torch.einsum('bhij,bhjd->bhid', attn, v)
# out:b, 64, 65*8
out = rearrange(out, 'b h n d -> b n (h d)')
# out:b, 64, 1024
out = self.to_out(out)
return out
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout):
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(nn.ModuleList([
Residual(PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout))), #自注意+layernorm+残差连接
Residual(PreNorm(dim, FeedForward(dim, mlp_dim, dropout = dropout))) #FFN+layernorm+残差连接
]))
def forward(self, x, mask = None):
for attn, ff in self.layers: #通过每一层编码器
x = attn(x, mask = mask)
x = ff(x)
return x
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
#image_size为输入图片的尺寸(H==W)
#patch_size为分块的尺寸(p)
#num_classes为类数
#dim为图片编码行向量进行线性变换后的维数
#depth为transformer中编码器层数
#heads为自注意头数
#mlp_dim为FFN隐藏层大小
#pool参数决定使用一张图片中所有编码行向量的均值向量来进行分类,还是只使用token向量来分类
#channels为图片通道数
#dim_head为W_k、W_q、W_v矩阵的输出维数
#dropout为在transformer过程中的dropout
#emb_dropout为在编码过程中的dropout
super().__init__()
assert image_size % patch_size == 0, 'Image dimensions must be divisible by the patch size.' #H=W需要可以整除p
num_patches = (image_size // patch_size) ** 2 #num_patches表示一张图片编码行向量的个数
patch_dim = channels * patch_size ** 2 #patch_dim表示编码行向量的长度
assert num_patches > MIN_NUM_PATCHES, f'your number of patches ({num_patches}) is way too small for attention to be effective (at least 16). Try decreasing your patch size' #防止num_patches太小
assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
self.patch_size = patch_size
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim)) #初始化位置编码
self.patch_to_embedding = nn.Linear(patch_dim, dim) #线性变换层E
self.cls_token = nn.Parameter(torch.randn(1, 1, dim)) #初始化token向量
self.dropout = nn.Dropout(emb_dropout)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)
self.pool = pool
self.to_latent = nn.Identity()
self.mlp_head = nn.Sequential(nn.LayerNorm(dim),nn.Linear(dim, num_classes)) #输出层,包括一个layernorm和一个全连接网络
def forward(self, img, mask = None):
p = self.patch_size
x = rearrange(img, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = p, p2 = p) #图片分块
x = self.patch_to_embedding(x) #线性变换层E降维
b, n, _ = x.shape
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b = b) #token向量扩增到与batch中图片相同的数目
x = torch.cat((cls_tokens, x), dim=1) #连接上token向量
x += self.pos_embedding[:, :(n + 1)] #加上位置编码
x = self.dropout(x) #编码时dropout
x = self.transformer(x, mask) #transformer
x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0] #pool参数决定使用一张图片中所有编码行向量的均值向量来进行分类,还是只使用token向量来分类
x = self.to_latent(x)
return self.mlp_head(x) #输出层