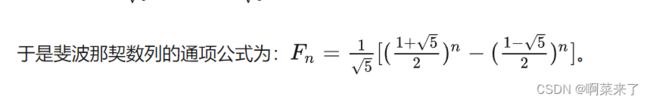蓝桥杯python组--基础训练---求输入的第n个，斐波那契数

题目

求输入的第n个，斐波那契数

斐波那契数：斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

思路1：

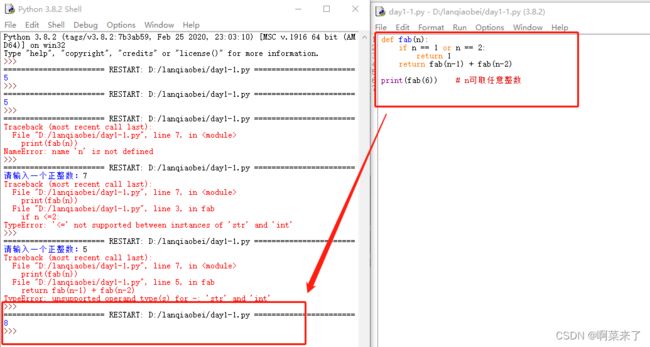
递归
当n=1或n=2时，F=1。即F（0）=0，F（1）=1，F（2）=1;n>=2时，F(n)=F(n - 1)+F(n - 2)，n ∈ N*

def fab(n):
    if n == 1 or n == 2:
        return 1
    return fab(n-1) + fab(n-2)

print(fab(6))    # n可取任意整数

结果

思路2：

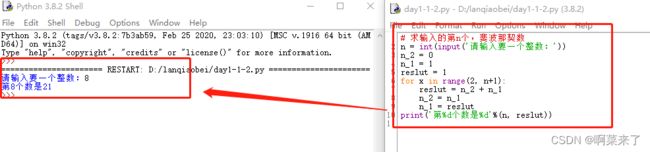
for循环
先令第0个和第1个数为1
再进入for循环后，从第二个数开始。

# 求输入的第n个，斐波那契数
n = int(input('请输入要一个整数：'))
n_2 = 0
n_1 = 1
reslut = 1
for x in range(2, n+1):
    reslut = n_2 + n_1
    n_2 = n_1
    n_1 = reslut
print('第%d个数是%d'%(n, reslut))

结果

思路3

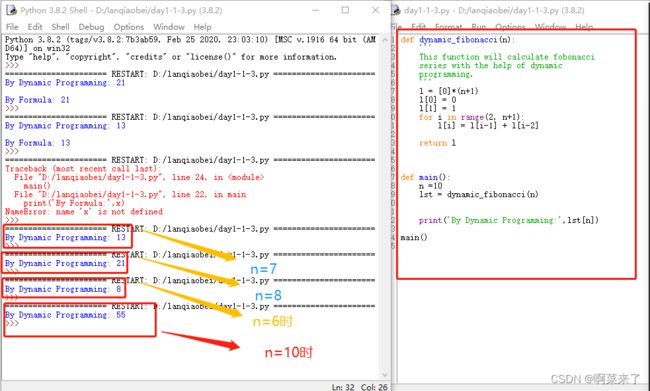
动态编程

def dynamic_fibonacci(n):
    '''
    This function will calculate fobonacci
    series with the help of dynamic
    programming.
    '''
    l = [0]*(n+1)
    l[0] = 0
    l[1] = 1
    for i in range(2, n+1):
        l[i] = l[i-1] + l[i-2]
    return l
def main():
    n =10
    lst = dynamic_fibonacci(n)
    print('By Dynamic Programming:',lst[n])
main()

结果

思路4

公式法
在这种方法中，我们借助公式计算斐波纳契数列的第n个项。

Formula:
phi = ( 1 + sqrt(5) ) / 2
An = phin/ sqrt(5)

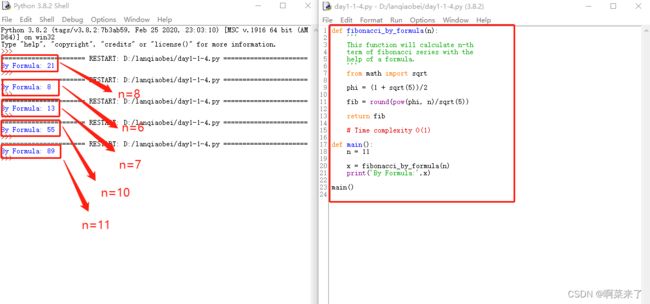
def fibonacci_by_formula(n):
    '''
    This function will calculate n-th
    term of fibonacci series with the
    help of a formula.
    '''
    from math import sqrt
    phi = (1 + sqrt(5))/2
    fib = round(pow(phi, n)/sqrt(5))
    return fib
    # Time complexity O(1)
 
def main():
    n = 1
    x = fibonacci_by_formula(n)
    print('By Formula:',x)
 
main()

结果

思路5

生成器法

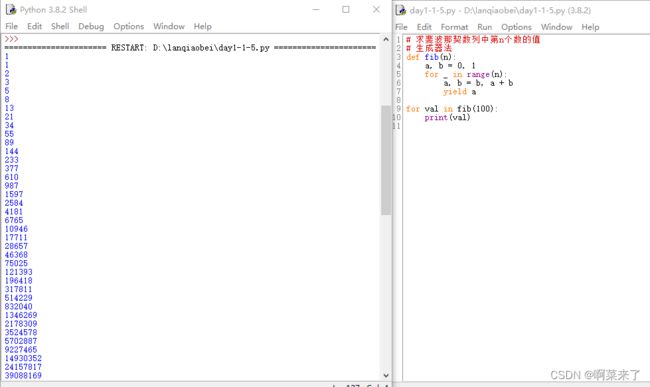
# 求斐波那契数列中第n个数的值
# 生成器法
def fib(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
        yield a
        
for val in fib(100):
    print(val)

结果

生成100个结果。
由于界面有限，只截图部分结果。

思路6

集合法
1、定义空的列表和sum
2、判断是否为第一项或第二项，如果是，则直接在列表中添加1（因为前两项的值都为1）
3、从第三项开始，则要用我们的算法开始计算（本项=前2项+前一项），前两项比较特殊，直接制定前两项
4、遍历集合，将集合中的每一个元素值都加到Sum中
5、打印输出

""
求斐波那契数列第n项以及前n项和
斐波那契数列：从第二项开始，每一项都等于前两项之和
1,1,2,3,5,8,13,21,34,55,89,144，...
""

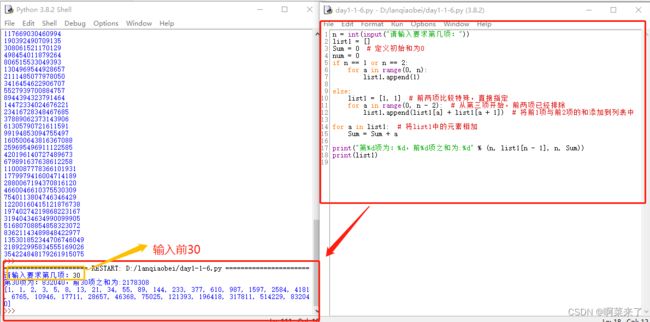
n = int(input("请输入要求第几项："))
list1 = []
Sum = 0  # 定义初始和为0
num = 0
if n == 1 or n == 2:
    for a in range(0, n):
        list1.append(1)

else:
    list1 = [1, 1]  # 前两项比较特殊，直接指定
    for a in range(0, n - 2):  # 从第三项开始，前两项已经排除
        list1.append(list1[a] + list1[a + 1])  # 将前1项与前2项的和添加到列表中

for a in list1:  # 将list1中的元素相加
    Sum = Sum + a

print("第%d项为：%d，前%d项之和为:%d" % (n, list1[n - 1], n, Sum))
print(list1)

结果