R语言聚类——KMeans家族（Simple K-Means、Sequential K-Means、Forgetful Sequential K-Means）

K-Means家族有三个算法：

1. Simple K-Means
2. Sequential K-Means
3. Forgetful Sequential K-Means

接下来我会简单介绍一下这几个算法，并分析它们的特点和优劣。

Simple K-Means

最简单的聚类算法就是K均值（Simple K-Means）算法。其核心思想如下：

假设有k个聚类（clusters），每个聚类有一个质心（centroid），其中质心是每个聚类中实例的均值（means），数据集中的每个点被指派给与该点距离（distance）最近的质心所在的聚类。

1. 首先估计每个聚类的中心（means）：m1，m2 …mk
2. 在所有中心（m1-mk）都不变前循环以下步骤：
   1）将每个实例分配到最距离最近的中心的聚类中；
   2）计算每个聚类新的均值，并更新m1-mk的值。

以下为迭代次数为6的kMeans聚类的例子，每个“+”为当前迭代的聚类质心，第一次迭代的质心为随机估计值。

R语言代码实现

其中，参数clusterNum为最后需要聚类的个数，maxLiteration为最大迭代次数，clusters为预先生成的数据集（生成方式见上一篇笔记）

# K-Means
kMeans <- function(clusterNum, maxLiteration,clusters) {
    # The condition of whether the loop ends
    END = FALSE
    # Count the literation times
    literation = 0

    # 'centers' is a matrix with randomly choosed centroids
    centers <- clusters[sample(nrow(clusters), clusterNum, replace = F), c("x", "y")]
    centers <- cbind(centers, cname = c(1:clusterNum))

    # The function find the closest centroid to the vector and assign the vector to the cluster
    # This function is used by apply()
    kMeansAssignCluster <- function(x, centers) {
        minDist <- 10e10
        centerIndex <- 0
        for (center in 1:nrow(centers)) {
            dist <- dist(rbind(x, centers[center,]))
            if (dist < minDist) {
                minDist <- dist
                centerIndex <- center
            }
        }
        centers[centerIndex, "cname"]
    }

    # Keep looping when not receiving END sign and literation times lower than 100
    while (!END & literation < maxLiteration) {
        # Assign each vector to the closest cluster
        av <- apply(clusters[, c("x", "y")], 1, kMeansAssignCluster, centers = centers)
        # Store the assigned result into data set
        clusters <- data.frame(clusters[, c("x", "y", "label")], assign = as.character(av))

        END <- TRUE
        # Recalculate the centroids, if different from the previous one, update them and keep looping
        for (assignCluster in 1:clusterNum) {
            newCenter <- round(apply(clusters[clusters$assign == as.character(assignCluster), c("x", "y")], 2, mean))
            dif <- centers[assignCluster, c("x", "y")] - newCenter
            if (mean(as.matrix(dif)) != 0) {
                END <- FALSE
                centers[assignCluster, c("x", "y")] <- newCenter
            }
        }
        literation <- literation + 1
    }

    print(literation)
    # Draw the diagram
    print(ggplot(data = clusters, mapping = aes(x = x, y = y, shape = label, color = assign)) + geom_point()+ labs(title = "K-means"))
}

Sequential K-Means

它与Simple K-Means的区别在于，它使用了增量更新的策略。即其优势在于：

1. 每次获取一个新的实例（example）都更新一次均值，而k-means是将所有实例分配完后更新均值。
2. 可以实现在获取所有实例之前就开始聚类。

其核心思想如下：

1. 首先估计每个聚类的中心（means）：m1，m2 …mk；
2. 设置计数器（count）：n1，n2 … nk 的值为0；
3. 在所有中心（m1-mk）都不变前循环以下步骤：
   1）获取一个新的实例（example）x；
   2）若mi的距离与x最近：将计数器ni加1且将mi替换为mi+1/n(x-mi)。

R语言代码实现

# Sequential K-Means
SequentialKMeans <- function(clusterNum,maxLiteration) {
    # The condition of whether the loop ends
    END = FALSE
    # Count the literation times
    literation = 0
    n <- numeric(clusterNum)

    # 'centers' is a matrix with randomly choosed centroids
    centers <- clusters[sample(nrow(clusters), clusterNum, replace = F), c("x", "y")]
    centers <- cbind(centers, cname = c(1:clusterNum))

    # Keep looping when not receiving END sign
    while (!END) {
        for (vector in 1:nrow(clusters)) {
            x <- clusters[vector, c("x", "y")]
            minDist <- 10e10
            centerIndex <- 0
            for (center in 1:nrow(centers)) {
                dist <- dist(rbind(x, centers[center, c("x", "y")]))
                if (dist < minDist) {
                    minDist <- dist
                    centerIndex <- center
                }
            }
            n[centerIndex] <- n[centerIndex] + 1
            # Update Center
            centers[centerIndex, c("x", "y")] <- centers[centerIndex, c("x", "y")] + (1 / n[centerIndex]) * (x - centers[centerIndex, c("x", "y")])
            clusters[vector, "assign"] <- as.character(centers[centerIndex, "cname"])
        }
       
        literation <- literation + 1
        if (literation >= maxLiteration) {
            END <- TRUE
        }
    }
    print(ggplot(data = clusters, mapping = aes(x = x, y = y, shape = label, color = assign)) + geom_point() + labs(title = "Sequential K-means"))
}

Forgetful Sequential K-Means

它与Sequential K-Means的区别在于，它不再进行计数，而是将n/1替换为一个常数a（即替换mi = mi+a(x-mi)）。则有：

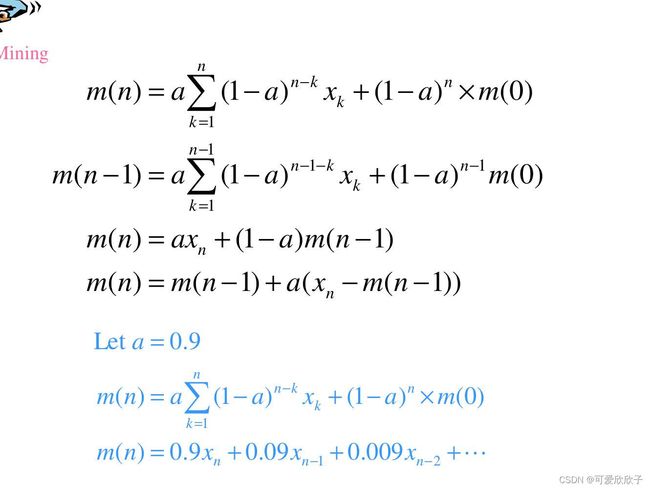
由上图可见，“Forgetful”体现在，越往后面的实例权重越高，因此最初的m0会被渐渐“遗忘”。
因此，Forgetful Sequential K-means比较适合问题随时间不断改变的情况。

因为Forgetful Sequential K-means的代码与Sequential K-means的几乎一样，只需要取消计数并把质心的更新参数换成常数a，所以这里不再放出。

K-Means家族算法在各类型数据集上的表现

数据集为用上一篇文章生成的数据集，分别使用上面的代码对它们进行聚类，以下是Simple K-means和Sequential K-means的表现：

1. 重叠（Overlapping）
   
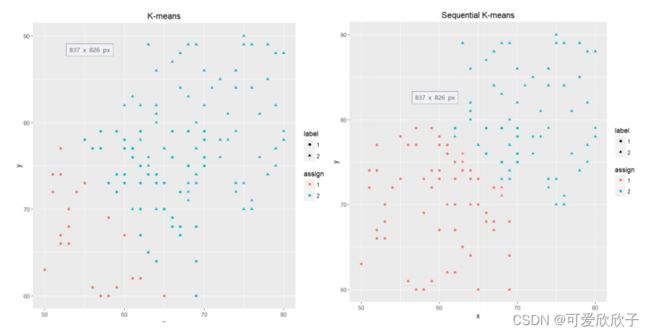
2. 噪声（Noise）
   
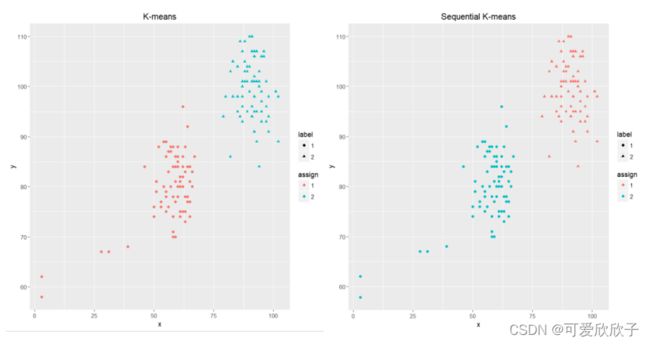
3. 环形
   
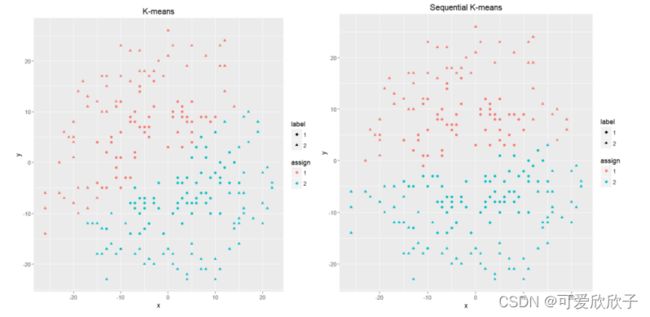
   由结果可见，K-Means家族的算法不太适合重叠（Overlapping）的聚类，但在有噪声的聚类下表现还不错。另外K-Means不太适合不同形状的聚类，因为所有聚类最后都是一团一团的。

K-Means聚类需要关注的问题

1. 空聚类

由于更新质心时需要计算每个实例的平均值，即m=1/n(x1+…+xn)，而n取决于有多少实例被分配到该聚类。因此有可能出现某个聚类一个实例都没有的情况，这在计算中会出现问题，即n=0且n为分母。
解决方式为：可以将n=0的质心替换为一个比较大的聚类中的一个点。（这在我的代码中没有体现，但加上去也不难，暂时没加）

3. 初始质心的选择

实验表明，初始质心的选择会极大影响到聚类效果，但初始质心需怎么估计呢？

1. 一个方式为选择比需要的聚类个数更大的k，聚类完成后再通过后处理（post-processing）合并一些类;
2. 勤奋！多跑几次找到效果最好的~

5. 离群点（Outliers）

离群点也会影响k-means的效果，因为它们会在迭代过程中把质心拉偏。
所以数据预处理很重要！把离群点弄走，或者标准化数据~

7. k值的选择

如何确定合适的k值？
数据后处理（post-processing）
把小的聚类丢掉
分开数据分布很松散的聚类，合并数据分布紧密的聚类。