八皇后问题初始思路python_『算法』『数据结构』 浅谈回溯算法（DFS 深度优先算法），理解程序员必懂必会的计算机常见算法——回溯算法（DFS 深度优先算法）...

文章目录

基本认识

基本思想与原理

适用的问题

求解的步骤与模板

回溯函数的三个组成部分：

回溯函数万能模板：

引例部分

实战部分

趁热打铁 刷题练习部分(持续更新)

基本认识

回溯算法(DFS 深度优先算法)实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

基本思想与原理

回溯法(DFS 深度优先算法)简单来说就是按照深度优先的顺序，穷举所有可能性的算法，但是回溯算法比暴力穷举法更高明的地方就是回溯算法可以随时判断当前状态是否符合问题的条件。一旦不符合条件，那么就退回到上一个状态，省去了继续往下探索的时间。

换句话说，回溯法可以理解为通过选择不同的岔路口寻找目的地，一个岔路口一个岔路口的去尝试找到目的地。如果走错了路，继续返回来找到岔路口的另一条路，直到找到目的地。省去了在错路上走下去的时间。

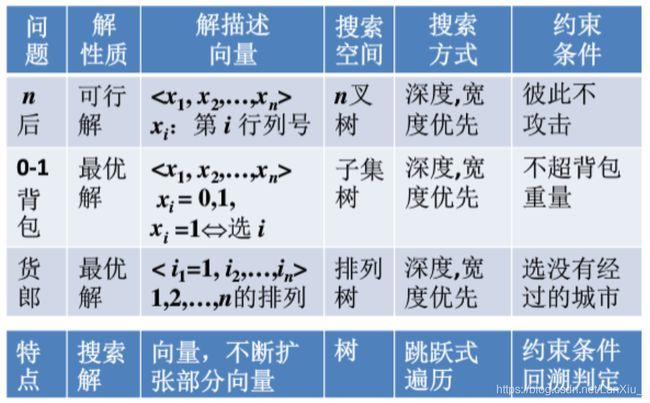
适用的问题

如果一个问题是搜索求解类的问题，而且该问题的解是树状结构(不断扩张式向量)，该题就可以考虑使用回溯算法。

加粗样式

求解的步骤与模板

回溯函数的三个组成部分：

1.回溯出口：当找到了一个问题的解时，存储该解。

2.回溯主体：就是遍历当前的状态的所有子节点，并判断下一个状态是否是满足问题条件的，如果满足问题条件，那么进入下一个状态。

3.状态返回：如果当前状态不满足条件，那么返回到前一个状态。

回溯函数万能模板：

以python3为例：

def backtrack ( 参数 ):

#回溯出口

if ( 满足题意了 ):

计数或进行其他操作

return True #有时可以省略

#回溯主体

for( 查找当前节点的周围的节点 )

进行其他的操作;

标记已经搜索过的节点

backtrack( 下一次搜索的节点 )

#状态返回

取消标记;

return False#有时可以省略

引例部分

八皇后问题：

八皇后问题是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法？

解题思路：

1.从棋盘的第一行开始，从第一个位置开始，依次判断当前位置是否能够放置皇后，判断的依据为：同该行之前的所有行中皇后的所在位置进行比较，如果在同一列，或者在同一条斜线上(斜线有两条，为正方形的两个对角线)，都不符合要求，继续检验后序的位置。

2.如果该行所有位置都不符合要求，则回溯到前一行，改变皇后的位置，继续试探。

3.如果试探到最后一行，所有皇后摆放完毕，则直接打印出 8*8 的棋盘。最后一定要记得将棋盘恢复原样，避免影响下一次摆放。

实战部分

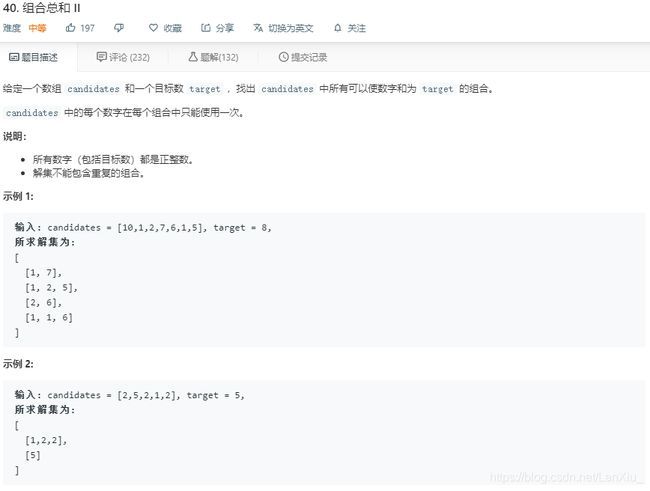
组合总数Ⅱ问题：

解题思路：

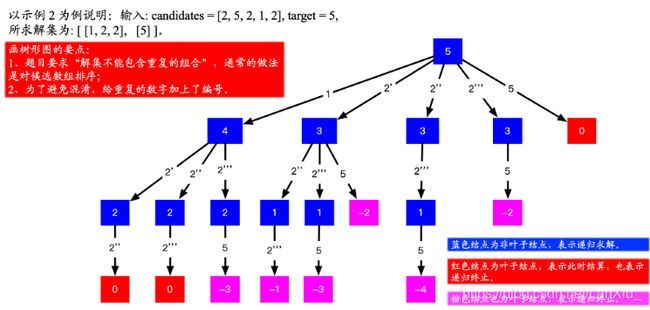
这道题的思路是：以 target 为根结点，依次减去数组中的数字，直到小于0或者等于0，把等于0的结果记录到结果集中。

“解集不能包含重复的组合”，就提示我们得对数组先排个序(“升序”或者“降序”均可，下面示例中均使用“升序”)。

“candidates 中的每个数字在每个组合中只能使用一次”，那就按照顺序依次减去数组中的元素，递归求解即可：遇到0就结算且回溯，遇到负数也回溯。

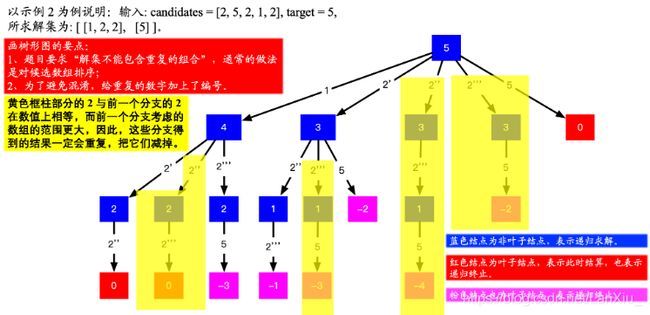
candidates 中的数字可以重复，可以借助「LeetCode」第 47 题：“全排列 II”(后面刷题练习部分有链接) 的思想，在搜索的过程中，找到可能发生重复结果的分支，把它剪去。

下面附上Python3的题解代码

class Solution:

def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:

l=len(candidates)

if l==0:

return []

candidates.sort() #初始化

path=[]

res=[]

def backtrack(begin,path,target):

if target==0: #回溯出口

res.append(path[:])

for i in range(begin,l): #回溯主体

target_next=target-candidates[i] #剪枝操作

if target_next<0:

break

if i>begin and candidates[i-1]==candidates[i]:

continue

path.append(candidates[i])

backtrack(i+1,path,target_next)

path.pop() #状态返回

backtrack(0,path,target)

return res

趁热打铁 刷题练习部分(持续更新)

以下是LeetCode题库中一些用到回溯算法的经典例题的题目及解析，有题干，有题解代码、有解题思路(持续更新)：

No.17.电话号码的字母组合：

https://blog.csdn.net/LanXiu_/article/details/104085787

No.22.括号生成:

https://blog.csdn.net/LanXiu_/article/details/104103922

No.37.解数独:

https://blog.csdn.net/LanXiu_/article/details/104176266

No.39.组合总和:

https://blog.csdn.net/LanXiu_/article/details/104176266

No.40.组合总和Ⅱ:

https://blog.csdn.net/LanXiu_/article/details/104176266

No.44.通配符匹配:

https://blog.csdn.net/LanXiu_/article/details/104177349

No.46.全排列:

https://blog.csdn.net/LanXiu_/article/details/104177432

No.47.全排列Ⅱ:

https://blog.csdn.net/LanXiu_/article/details/104177432