密码学实践-读书笔记六七
第六章 Hash函数
Hash函数可以用于认证、构造数字签名方案。
(大多数数字签名用于公钥运算的开销大,直接对这个消息本身签名不经济,因此可以先对消息m做hash,然后对h(m)进行签名。)
输入是任意长度的比特或字节串,输出是固定长度(128比特到512比特之间)的对应串。
用于签名的hash函数满足的条件:构造两个消息m1、m2使得h(m1)=h(m2)是不可能的。
6.1 Hash函数的安全性:
基本要求:单向函数(不可逆)
抗碰撞性(不同的m有相同的摘要,尽管存在但是不可能找到),可以用于数字签名
理想Hash函数:从所有可能的输入值到有限可能的输出值集合的一个随机映射。(然而没有这样随机映射的Hash函数)
对hash函数的攻击是一个非平凡区分hash函数与理想hash函数的方法,常规攻击似乎寻找碰撞的生日攻击:对具有n比特输出的Hash函数,生日攻击大约需要2n/2步。
• 在一个会场参加会议的人中,找一个与某人生日相同的概率超过0.5时,所需参会人员为183人。但要问使参会人员中至少有两个同日生的概率超过0.5的参会人数仅为23人。
• Pt=(1-1/365)(1-2/365)…(1-(t-1)/365)
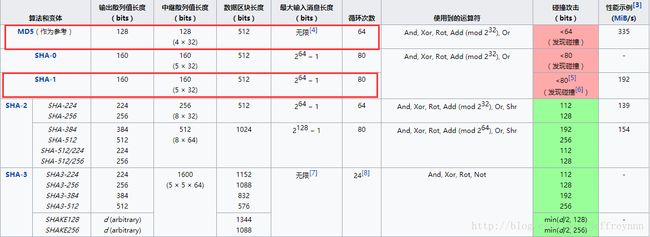
6.2 MD5:
输入:任意长度
输出:128比特消息摘要
分组长度:512比特(64字节)块序列(最后一个块填充)
有4个(字)变量A、B、C、D均为32比特作为状态变量(上课时学的是初始化变量)
对512比特按每组32比特进行分组M[0],M[1]……M[15]。
共进行4轮压缩
MD5的128比特长度是不够的,进行264次计算就可以找到一个碰撞,对于现代密码是不够的。
SHA-1:
(安全HASH算法)
输入:任意长度
输出:160比特
速度比MD5慢2~3倍
• 步驟 1:將输入明文(512 bits)以每 32 bits 為单位,分別存入M[k]中,其中 k =0, 1, 2, .., 15,Wt由M[k]扩展
• 步驟 2:初始化 A、B、C 与 D 缓存器,如下:
A:67 45 23 01 B:EF CD AB 89 C:98 BA DC FE
D:10 32 54 76 E :C3 D2 E1 F0
• 步驟 3:进入第一回合运算,执行 20 次:
a,b,c,d,e→(e+f1(t,b,c,d)+S5(A)+Wt+Kt),A,S30(B),C,D)
• 步驟 4:进入第二回合运算,执行 20 次:
a,b,c,d,e→( e+f2(t,b,c,d)+S5(A)+Wt+Kt),A,S30(B),C,D)
• 步驟 5:进入第三回合运算,同样执行 20 次:
a,b,c,d,e→( e+f3(t,b,c,d)+S5(A)+Wt+Kt),A,S30(B),C,D)
• 步驟 6:进入第四回合运算,同样执行 20 次:
a,b,c,d,e→( e+f4(t,b,c,d)+S5(A)+Wt+Kt),A,S30(B),C,D)
• 步驟 7:输出消息摘要,执行 SUM32 计算。
注:W0,W1,……W15等于消息M[0],M[1],…,M[15].其余的:
• Wt=S1(M[t-16]⊕M[t-14]⊕M[t-8]⊕M[t-3])
SHA-1问题是:输出长度为160比特,仅用280步就可以得到碰撞,远低于密钥长度为128~256比特的需要。
SHA-256、SHA-384、SHA-512分别是256、384、512比特的输出,与密钥长度为128、196、256比特的AES一起使用,运算时间也是逐级增加。
6.3 HASH函数的缺陷
1、长度扩充问题:消息m’的前k个块与消息m的前k个块相同,即h(m)是计算h(m’)的一个中间值。
长度扩充问题的存在是因为Hash函数计算的最后缺少一个特殊的处理过程,结果导致h(m)恰好是计算h(m’)时完成前k个块计算的中间状态。
攻击者得以扩充消息的长度,并为新的伪造消息计算出合法的散列摘要。

2、部分消息碰撞:
由于Hash函数的迭代结构,只要出现了碰撞,余下的输入均一样,则Hash值一定相同。
攻击者可以通过生日攻击用大约2n/2 步找到两个消息m和m’使得Hash函数发生碰撞,并使系统对消息m进行认证,然后用消息m’替代。因为m与m’有相同的hash值,因此对于任意的X,有h(m||X) = h(m’||X)。
6.4 修正方法:
对于这些问题可以使用两次Hash解决问题,![]() ,将h(m)放在Hash运算的前面,可以保证Hash函数的迭代运算与消息的每一个比特都有关,从而避免了长度扩充与部分碰撞的攻击。
,将h(m)放在Hash运算的前面,可以保证Hash函数的迭代运算与消息的每一个比特都有关,从而避免了长度扩充与部分碰撞的攻击。
![]()
缺点:速度慢,需要进行两次Hash运算需要存储整个消息
更正式的定义:
![]()
hd与hDBL都消除了长度扩充缺陷,但hDBL是否拥有n比特的安全有待证明,但两者都有n/2比特的安全性。
第七章 消息认证码(MAC)
用于防止对消息进行篡改。加密使Eve不能获取消息的内容,但不能阻止对消息进行篡改。
MAC是有两个输入的函数,其中一个是固定的密钥K,另一个是任意大小的消息m。
MAC(K,m),将消息m与MAC值一同发送。
理想的MAC函数是一个从所有可能的输入到n比特的输出的随机映射。
7.1 MAC的安全性:
系统的其他部分具有的缺陷会给攻击者泄露密钥K的部分信息。
K是攻击者掌握的关于密钥K的不确定性
定义:设n是MAC函数的大小,k是密钥K的以比特为单位的不确定性,对MAC函数的攻击是一个在2min(n,k)步内区分MAC函数和理想MAC函数的非平凡方法。
7.2 CBC-MAC
将分组密码转变为MAC函数的方法
采用的方法是对消息m用CBC模式进行加密,只保留最后一个消息块的密文,其余的丢弃

在CBC-MAC中,MAC值等于最后一个密文块,所以在CBC加密和CBC-MAC认证中使用相同的密钥特别危险。
一个简单的碰撞行为:设M是一个CBC-MAC 函数,如果已知M(a)=M(b),则对任意的c都有M(a||c)= M(b||c)。
![]()
攻击过程:
第一阶段:攻击者收集大量的MAC值,直到产生碰撞,即得到两个消息a与b且满足M(a)=M(b)。
第二阶段:若攻击者得到了发送者对消息a||c 的认证,他就可以用b||c 代替消息a||c而不用改变MAC的值。这就可以通过接收者对MAC值的认证。
不能直接对消息使用MAC函数,否则会导致简单的攻击存在:
1、 从L||m构造比特串,其中L是消息m在固定长度格式下编码的长度。
2、 对s进行填充使得其长度为分组大小的整数倍
3、 对填充后的s应用CBC-MAC
4、 输出最后一个密文或它的一部分,切记不要出输出中间的值。
CBC-MAC的优点,它与分组密码有相同的计算过程。
7.3 HMAC
用Hash函数构造MAC函数。
长度扩充:当知道MD5(secret)时,在不知道secret的情况下,可以很轻易地推算出MD5(secret||padding||m’)。
长度扩展的理论基础就是将已知的压缩后的结果,直接拿过来作为新的压缩输入。因此只需要知道上一次压缩后的结果,而不需要知道原来的消息内容是什么。
HMAC计算h(K^a||h(K^b||m)),其中a与b是指定的常量,即首先对消息进行一次Hash运算,然后再对结果和密钥进行Hash运算。
UMAC:提出了一个思想,用密钥的不确定性提高MAC速度,值得深入研究。
7.4 MAC的使用
攻击:Eve可以记录从Alice到Bob的消息,然后在以后的某个时间给Bob发送这个消息的一个副本,当Bob收到这个副本,那么就会当作是Alice发送过来的。
Alice与Bob不仅想对消息m进行认证,而且包括附加数据d。这个附加数据包括防止重放攻击的消息数,还有消息源和目的地等。因此MAC必须认证d和m。
设计准则:Horton原则:认证消息的内容,而不是消息本身。
MAC认证的不仅是消息m,而是m以及Bob在解释时所需的所有信息,这应该包括协议的标识符、协议的版本号以及消息的标识符和各个数据域的大小等信息。
Htoton原则说明了为什么低层的认证协议不能为高层的西医提供适当的认证。在IP包层的认证系统不能知道E-mail程序如何翻译数据,这就将它排除在检测消息的一致性之外。唯一的解决方案就是,在低层进行认证外让E-mail程序提供自己的数据交换认证。