nndl作业3
过程推导 - 了解BP原理
借用pattern recognition and machine learning里的




再次借用西瓜书和南瓜书里的推导:
数值计算 - 手动计算,掌握细节
代码实现 - numpy手推 + pytorch自动
借用斋藤康毅了老师的代码:(https://github.com/oreilly-japan/deep-learning-from-scratch-3/wiki/Errata)
numpy:
对比【numpy】和【pytorch】程序,总结并陈述。
使用斋藤康毅老师的代码:
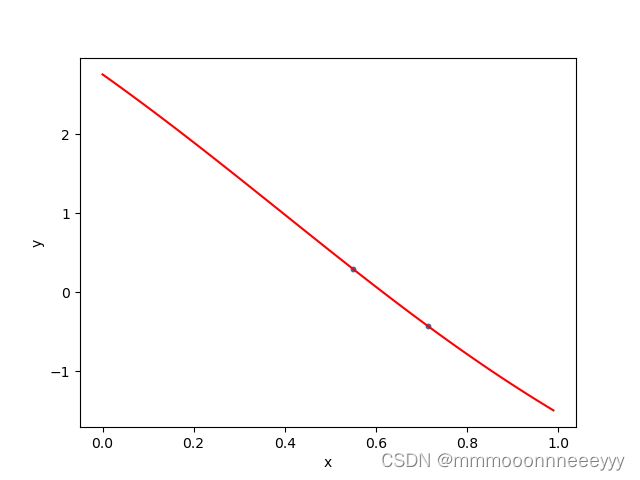
这是step43的双线性层的拟合:
import numpy as np
import matplotlib.pyplot as plt
from dezero import Variable
import dezero.functions as F
np.random.seed(0)
x = np.random.rand(2, 1)
y = np.sin(2 * np.pi * x) + np.random.rand(2, 1)
I, H, O = 1, 10, 1
W1 = Variable(0.01 * np.random.randn(I, H))
b1 = Variable(np.zeros(H))
W2 = Variable(0.01 * np.random.randn(H, O))
b2 = Variable(np.zeros(O))
def predict(x):
y = F.linear(x, W1, b1)
y = F.sigmoid(y)
y = F.linear(y, W2, b2)
return y
lr = 0.2
iters = 10000
for i in range(iters):
y_pred = predict(x)
loss = F.mean_squared_error(y, y_pred)
W1.cleargrad()
b1.cleargrad()
W2.cleargrad()
b2.cleargrad()
loss.backward()
W1.data -= lr * W1.grad.data
b1.data -= lr * b1.grad.data
W2.data -= lr * W2.grad.data
b2.data -= lr * b2.grad.data
if i % 1000 == 0:
print(loss)
print(W1.data,'\n',W2.data,'\n',b1.data,'\n',b2.data)
# Plot
plt.scatter(x, y, s=10)
plt.xlabel('x')
plt.ylabel('y')
t = np.arange(0, 1, .01)[:, np.newaxis]
y_pred = predict(t)
plt.plot(t, y_pred.data, color='r')
plt.show()
variable(0.13810752213721122)
variable(0.131863649256508)
variable(0.02077943406953136)
variable(0.00021353515288145218)
variable(1.2480437908055901e-08)
variable(6.788420408258309e-13)
variable(3.690166492633276e-17)
variable(2.0059443785614088e-21)
variable(1.0883843035112346e-25)
variable(3.301043924679722e-29)
W1,W2,b1,b2[[ 4.01292788 -0.21641021]]
[[-4.40329299]
[ 0.62341179]]
[-2.43843046 0.08405058]
[1.93751242]
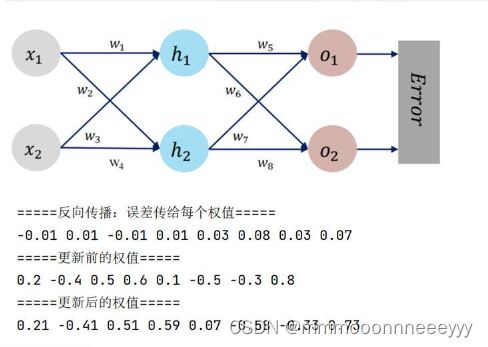
激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
import torch
x = torch.tensor([0.5,0.3])
weights = torch.tensor([0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8])
y = torch.tensor([0.23, -0.07])
print('inputs={}'.format(x))
print('weights={}'.format(weights))
print('real outputs={}'.format(y))
model = torch.nn.Sequential(
torch.nn.Linear(2,2,False),
torch.nn.Sigmoid(),
torch.nn.Linear(2,2,False),
torch.nn.Sigmoid()
)
model[0].weight.data = weights[[0,2,1,3]].reshape(2,2)
model[2].weight.data = weights[[4,6,5,7]].reshape(2,2)
optimizer = torch.optim.SGD(model.parameters(),1,momentum=0)
y_pred = model(x)
print('pred={}'.format(y_pred))
loss = (1 / 2) * (y_pred[0] - y[0]) ** 2 + (1 / 2) * (y_pred[1] - y[1]) ** 2
print('MSE loss={}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w1,w3,w2,w4:{}'.format(model[0].weight.data.detach().reshape(1,-1).squeeze()))
print('w5,w7,w6,w8:{}'.format(model[2].weight.data.detach().reshape(1,-1).squeeze()))
inputs=tensor([0.5000, 0.3000])
weights=tensor([ 0.2000, -0.4000, 0.5000, 0.6000, 0.1000, -0.5000, -0.3000, 0.8000])
real outputs=tensor([ 0.2300, -0.0700])
pred=tensor([0.4769, 0.5287], grad_fn=)
MSE loss=0.2097097933292389
w1,w3,w2,w4:tensor([ 0.2084, 0.5051, -0.4126, 0.5924])
w5,w7,w6,w8:tensor([ 0.0654, -0.3305, -0.5839, 0.7262])
激活函数Sigmoid改变为Relu,观察、总结并陈述。
import torch
x = torch.tensor([0.5,0.3])
weights = torch.tensor([0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8])
y = torch.tensor([0.23, -0.07])
print('inputs={}'.format(x))
print('weights={}'.format(weights))
print('real outputs={}'.format(y))
model = torch.nn.Sequential(
torch.nn.Linear(2,2,False),
torch.nn.ReLU(),
torch.nn.Linear(2,2,False),
torch.nn.ReLU()
)
model[0].weight.data = weights[[0,2,1,3]].reshape(2,2)
model[2].weight.data = weights[[4,6,5,7]].reshape(2,2)
optimizer = torch.optim.SGD(model.parameters(),1,momentum=0)
y_pred = model(x)
print('pred={}'.format(y_pred))
loss = (1 / 2) * (y_pred[0] - y[0]) ** 2 + (1 / 2) * (y_pred[1] - y[1]) ** 2
print('MSE loss={}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w1,w3,w2,w4:{}'.format(model[0].weight.data.detach().reshape(1,-1).squeeze()))
print('w5,w7,w6,w8:{}'.format(model[2].weight.data.detach().reshape(1,-1).squeeze()))
inputs=tensor([0.5000, 0.3000])
weights=tensor([ 0.2000, -0.4000, 0.5000, 0.6000, 0.1000, -0.5000, -0.3000, 0.8000])
real outputs=tensor([ 0.2300, -0.0700])
pred=tensor([0.0250, 0.0000], grad_fn=)
MSE loss=0.023462500423192978
w1,w3,w2,w4:tensor([ 0.2103, 0.5062, -0.4000, 0.6000])
w5,w7,w6,w8:tensor([ 0.1513, -0.3000, -0.5000, 0.8000])
损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
区别在于torch输出的是总体的误差。
损失函数MSE改变为交叉熵,观察、总结并陈述。
for i in [model[0],model[2]]:
print(i.weight)
Parameter containing:
tensor([[-0.8461, 0.8132],
[ 0.2497, 0.0015]], requires_grad=True)
Parameter containing:
tensor([[ 0.1395, 0.6233],
[ 0.0780, -0.0958]], requires_grad=True)
改变步长,训练次数,观察、总结并陈述。
当步长为10e-4到10e-6之间1000轮下降很慢,10e-4到10e-1下降很快下降到复数过大之后nan
还有特殊的情况下,loss会震荡之前看到分叉图
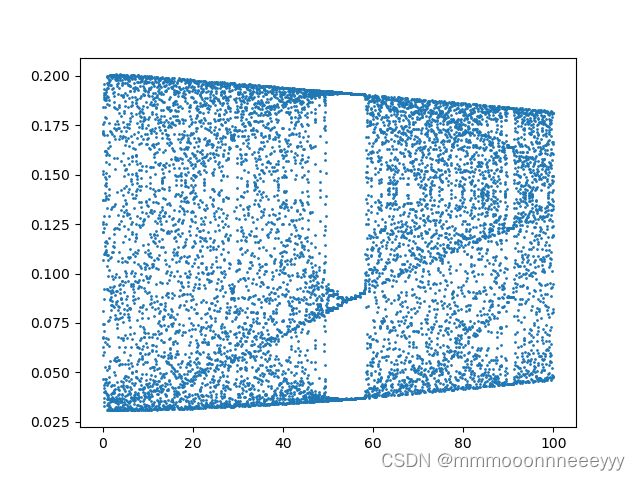
给个链接给个图自己玩玩,
https://zhuanlan.zhihu.com/p/565696464其实就是迭代过程中的函数的二次型的映射就会有形成,而激活函数并不改变
趋势,而两层的网络相当于二次型函数,加上参数在训练过程中可能的正态分布(相关帖子:https://www.zhihu.com/answer/2237211346)导致的loss的训练中的分布可能会‘震荡’
相关论文:
arXiv:2102.03793v3 [cs.LG] 23 Jun 2021
https://proceedings.neurips.cc/paper/2021/file/87ae6fb631f7c8a627e8e28785d9992d-Paper.pdf
权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
尽量不要初始化为0,可以使用高斯分布进行初始化
看相关帖子:https://www.zhihu.com/answer/909781841
权值w1-w8初始值换为0,观察、总结并陈述。
第一层的权重会变为零,所以要尽量不用全零进行初始化,但是偏置可以用零进行初始化。
全面总结反向传播原理和编码实现,认真写心得体会。
在自己造轮子中有很多的问题,其实在实现的过程中有很多的过程没有看到,从一开始的神经网络的结构到现在的结构有很多的变化。自己实现可以更加的理解数学过程,能够从数学到代码实现。