深度学习——CNN卷积神经网络个人理解笔记汇总
一、卷积神经网络
卷积神经网络包括:卷积层、激活函数、池化层、全连接层
通常把神经网络的隐藏层分为 卷积层和池化层
二、卷积层块
一般包括:卷积层+激活函数+汇聚层(池化层,又叫下采样层)
三、概念及作用
1)卷积层(Convolutional layer)
通过卷积操作(线性操作,即在原始图像上平移)对输入图像进行降维和特征提取
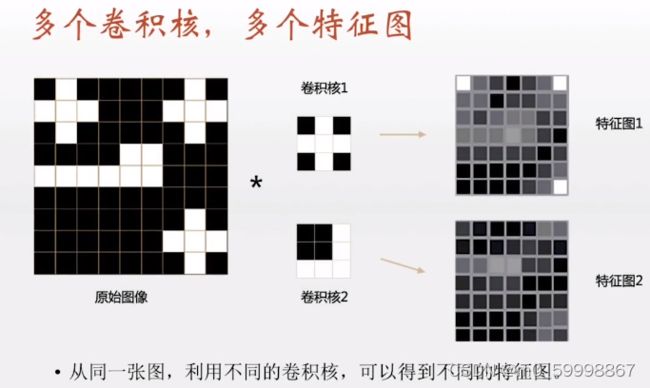
如图所示,卷积层实际上,就是按照模板(卷积核)的样子扫描原始图像,图像的每个区域通过与卷积核的内积,从而计算出扫描结果,得到结果图的像素点,也就是我们所说的特征图。
图像区域与卷积核相似度越高,内积的结果就越大,显示的像素点就越白,扫描完整个原图像,就得到一张完整的特征图。通过不同的卷积核,可以得到不同的特征图,最后多张特征图合在一起就成了一个立体图形,也就是所谓的卷积层
2)激活函数
用于加入非线性因素,将线性运算变成非线性,解决样本线性模型中不能解决的问题【sigmoid、tanh作激活函数,一定要对input,即输入进行归一化,否则激活后的值都会进入平坦区】
3)池化层(Pooling layer)
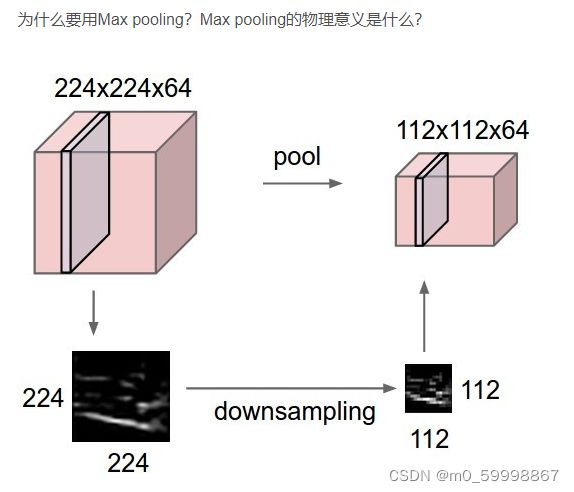
作用:特征提取(即删掉一些特征,通过去掉FeatureMap(特征图)中不重要的样本,进一步减少参数数量
如图:我们将卷积层经过2*2的池化,得到112*112*64的特征图,池化的作用是减少了参数集的作用,提取出关键特征(下图downsampling部分),去掉了大部分冗余信息。虽然这么做可能损失掉原图像中的某些信息,但在运算效率和渐变过程中起到了 作用。
4)全连接层(Fully-Connected layer)
全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用
卷积和池化相当于作特征工程,后面的全连接层相当于作特征加权,全连接层起到“分类器”的作用
注:(可学习)参数一般来自卷积层的卷积核和偏置项,激活函数层和汇聚层不产生参数
局部连接和全连接图像解析:
2、全连接
四、卷积神经网络参数个数分析
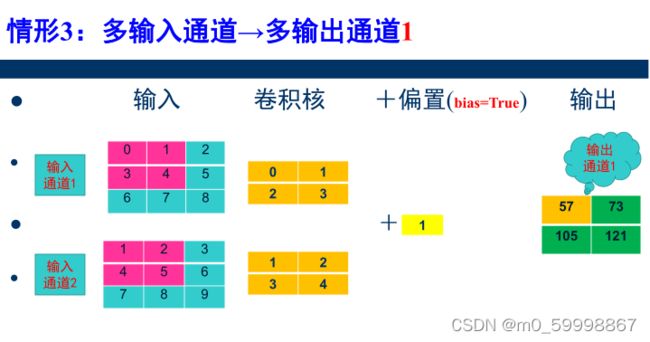
1)
2)
3)
4)
5)
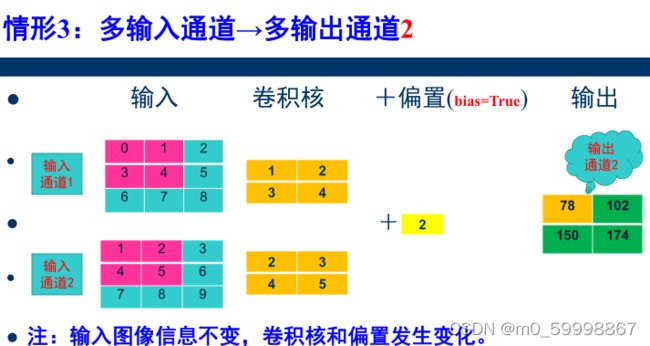
总结:多输入通道→多输出通道 参数计算公式:
Co × Ci × Kh × Kw + Co
其中,记Co为输出通道,Ci为输入通道,Kh为卷积核的高,Kw为卷积核的宽
五、神经网络结构的两个原则
平移不变性:不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应;
局部性:神经网络的前面几层应该关注输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系。
而卷积层和汇聚层可以较好地解决上述问题!!
六、softmax模型、多层感知机模型实现,Fashion-MNIST分类
将大小为28×28的图像展平为一个784固定长度的一维向量,然后用全连接层对其进行处理
局限性:
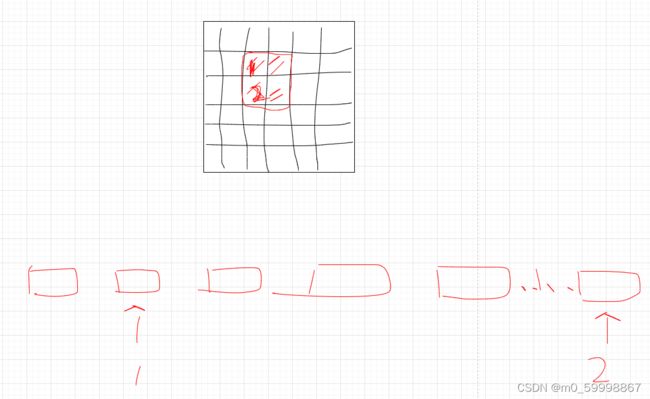
1)图像在同一列邻近的像素在这个一维向量中可能相距较远。它们构成的模式可能难以被模型识别
如图中原图像的1、2号像素相邻,展平为一维向量时,相隔就很远了,很难被模型识别
2)对于大尺寸的输入图像,使用全连接层容易导致模型过大(参数的存储空间过大)
这会带来过于复杂的模型和过高的存储开销
如何克服上述模型的局限性?
卷积神经网络
1)卷积层保留输入形状,使图像的像素在高和宽两个方向上的相关性均可能被有效识别
2)卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算,从而避免参数尺寸过大
(即局部连接和权值共享)
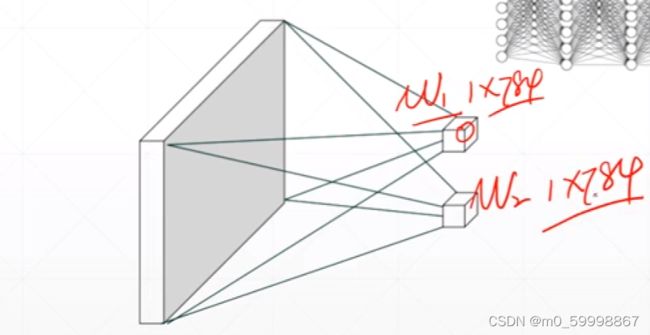
权值共享
如下图:最左侧的蓝色和绿色连接线,正常计算是2*6=12个参数(看卷积层计算,即红框内) ,但每个蓝线、绿线 是一样的,所有共有2个参数w1,w2,这就是权值共享。
3)汇聚层降低卷积层对位置的敏感性,同时降低对空间降采样表示的敏感性,(降低参数的作用)
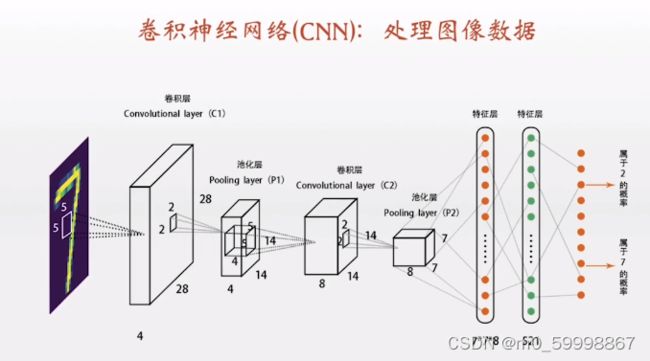
七、卷积神经网络(LeNet-5)
LeNet-5由两个部分组成:
卷积编码器:由两个卷积层组成
全连接层稠密块:由三个全连接层组成
卷积块中基本单元:5×5卷积层+sigmoid激活函数层+平均池化层
稠密块:三个全连接层,分别有120,、84和10个输出
图解:
![]()
卷积层块:
案列“手写数字识别”代码附在另一篇文章中,链接如下:
手写数字识别代码
参考文章:
卷积神经网络(卷积层,激活函数Relu,池化层,计算公式及API解释)
卷积神经网络——输入层、卷积层、激活函数、池化层、全连接层
部分资料来源于b站——集智学园