深度学习课程作业——手写数字识别（卷积神经网络）

本实验过程需要用到torchvision包，没有安装的小伙伴，windows用户可直接使用cmd命令，输入命令行pip install torchvision即可。【仍安装不了的，建议csdn直接查找安装教程】

---

一、加载数据集

1.1  导入实验可能用到的包、库等

#导入所需要的包
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import torch 
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from torch.autograd import Variable

%matplotlib inline

1.2  加载数据集

使用pytorch自带的数据加载器，包括dataset(装载数据集)，sampler（采样数据集），以及dataloader（迭代循环数据集）

#定义超参数
image_size = 28   #图像的总尺寸28*28
num_classes =10    #标签的种类数
num_epochs = 20   #训练的总循环周期
batch_size = 64  #一个撮批次的的等待小，64张图片


#加载MNIST数据，如果没有下载过，就会在当前路径下新建、data目录，并把文件存放在其中
#MNIST数据是属于torchvision包自带的数据，可以直接调用

#下载训练数据集
train_dataset=dsets.MNIST(root='./data',   #文件存储路径
                         train=True,     #提取训练集
                         transform=transforms.ToTensor(),   #转为tensor类型，便于数据预处理
                          download=True)       #找不到文件时，自动下载

#加载测试数据集
test_dataset = dsets.MNIST(root='./data',train=False,
                          transform=transforms.ToTensor())


#训练数据集的加载器，DataLoader方法，可以自动将数据分（批）割成batch，顺序随机打乱
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                         batch_size = batch_size,
                                         shuffle=True)

'''我们希望将测试数据分成两部分，一部分作为验证（校验）数据，一部分作为测试数据。
验证数据用于检测模型是否过拟合，并调整参数，测试数据检验整个模型的工作'''

#首先，我们定义下标数组indices，它相对于所有test_dataset中数据的代码
indices = range(len(test_dataset))
indices_val = indices[:5000]     #取前5000份作为验证集数据的下标
indices_test = indices[5000:]      #取后5000份作为测试集的下标


#根据这些下标，构造两个数据集的SubsetRandomSampler采样器
#校验集采样器的作用是：从数据集中indices_val，从indices_test抽取数据，它们会对下标进行采样
sampler_val = torch.utils.data.sampler.SubsetRandomSampler(indices_val)
sampler_test = torch.utils.data.sampler.SubsetRandomSampler(indices_test)

#根据两个采样器来定义加载器，注意将sampler_val和sampler_test分别赋值给validation_load和test_loadad
#采样器和加载器连接到一起，就可以在加载数据的时候随机抽取
validation_loader = torch.utils.data.DataLoader(dataset =test_dataset,
                                                batch_size =batch_size,
                                               sampler = sampler_val)

test_loader = torch.utils.data.DataLoader(dataset =test_dataset,
                                                batch_size =batch_size,
                                               sampler = sampler_test)

 这里提一个概念，在此作为笔记

下采样和上采样的区别：下采样就是缩小图像，在卷积神经网络中，池化层就是下采样，即对原图像进行减缩，使得原图像的某些信息被增强，丢弃多余的，冗余的信息

1.3  读取绘制手写数字图像

#随便从数据集中读入一张图片，并绘制出来
idx = 1001

#dataset支持下标索引，其中提取出来的每一个元素为features，target格式，即属性和标签
#因此train_dataset[idx][0] 表示取该元素中的features,即取第idx批次的features中第0个图像
muteimg = train_dataset[idx][0].numpy()

#由于一般的图像包含rgb三个通道，而MNIST数据集的图像都是灰度的，只有一个通道。
#用imshow画图，会将灰度矩阵自动展现为彩色，不同灰度对应不同颜色，从黄到紫

plt.imshow(muteimg[0,...])  #取muteimg中的28*28像素点画图
print('标签是：',train_dataset[idx][1])   #[idx][1]对应的是target
print(muteimg.shape)  #（1,28,28）

二、基本的卷积神经网络

2.1  构建网络

我们将要调用PyTorch强大的nn.Module这个类来构建卷积神经网络，我们分成如下几个步骤：
1.首先，我们构造ConvNet类，它是对类nn.Module的继承
2.接着，复写init，以及forward两个函数，第一个为构造函数，每当类ConvNet被具体化一个实例时，会被调用，forward则是在运行神经网络正向的时候被自动调用
3.自定义自己的方法
ConvNet其实也是一个大容器，它里面有Conv2d，MaxPool2d等组件

（按我自己理解就是，先构造定义卷积神经网络中的各种模块、函数，然后再拼接调用、实现真正的运算）

#定义卷积神经网络;4和8为人为指定的两个卷积层的厚度（feature map 的数量）
depth =[4,8]
class ConvNet(nn.Module):
    def __init__(self):
        #该函数在创建一个ConvNet对象的时候，即调用该语句：net=ConvNet()时，就会被调用
        #首先调用父类相应的构造函数
        super(ConvNet,self).__init__()
        
        #其次构造ConvNet需要用到的各个神经模块
        """注意，定义组件并没有真正搭建这些组件，只是把基本建筑砖块先找好"""
        self.conv1 = nn.Conv2d(1,4,5,padding=2)  #定义一个卷积层，输入通道为1，输出通道为4，窗口为5*5，填充为2
        self.pool = nn.MaxPool2d(2,2)  #定义一个Pooling层，一个窗口为2*2的pooling运算
        self.conv2 = nn.Conv2d(depth[0],depth[1],5,padding=2)  #第二层卷积，输入通道为depth[0]=4
        #输出通道为depth[1]=8,窗口为5*5，填充为2
        
        #一个线性连接层，输入尺寸为最后一层立方体
        self.fc1 = nn.Linear(image_size//4*image_size//4*depth[1], 512)
        
        #最后一层线性分类单元，输入为512，输出为要做分类的类别
        self.fc2 = nn.Linear(512,num_classes) 
    
    def forward(self,x):
        #该函数完成神经网络真正的前向运算，我们会在这里把各个组件进行实际的拼装
        #x的尺寸：（batch_size,num_filters,image_width,image_height）
        x = F.relu(self.conv1(x)) #第一层卷积，激活函数用Relu，为了防止过拟合
        #x的尺寸：（batch_size,num_filters,image_width,image_height）
        x = self.pool(x)
        
        #x的尺寸：（batch_size,depth[0],image_width,image_height)
        x = F.relu(self.conv2(x))  #第三层又是卷积，窗口为5，输入输出通道分别是depth[0]=4,depth[1]=8
        #x的尺寸：（batch_size,depth[1],image_width/2,image_height/2）
        x = self.pool(x)  #第四层poolings，将图片缩小到原大小的1/4
        
        
        #将立体的特征图Tensor压成一个一维向量
        #view用于tensor的指定重新排列
        #让x按照batch_size*(image_size//4)^2 * depth[1]的方式来排布向量
        x = x.view(-1,image_size//4*image_size//4*depth[1]) 
        #x尺寸：（batch_size,depth[1]*image_size//4*image_size//4）
        
        x = F.relu(self.fc1(x))  #第五层为全链接，Relu激活函数
        #x的尺寸：（batch_size,num_classes）
        
        x = F.dropout(x,training=self.training)  #以默认为0.5的概率为对这一层进行dropout操作
        x = self.fc2(x)  #全链接
        
        x = F.log_softmax(x,dim=1)  #输出层为log_softmax，即概率对数值log(p(x))
        return x
    
    def retrieve_features(self,x):
        #用于提取卷积神经网络的特征图，返回feature_map1,feature_map2为前两层卷积层的特征图
        feature_map1 = F.relu(self.conv1(x))  #完成第一层卷积
        x = self.pool(feature_map1)   #完成第一层pooling
        feature_map2 = F.relu(self.conv2(x))   #第二层卷积，两层特征图都存储到了feature_map1,feature_map2中
        return (feature_map1,feature_map2)
def rightness(predictions,labels):
    '''计算预测错误率的函数，其中predictions是模型给出的一组预测结果，batch_size、num_classes列的矩阵'''
    pred = torch.max(predictions.data,1)[1]  #对任意一行（一个样本）的输出值的第一个维度，求最大 
    rights = pred.eq(labels.data.view_as(pred)).sum() #将下标与labels中包含的类别进行比较，并累计得到总值
    return rights,len(labels)  #返回正确的数量和这一次一共比较了多少元素 

（之前记混或看不懂的地方）解释说明：

1.激活函数需作用于第五层全连接层，即fc1，而fc2不需被激活函数作用 。

2.经过两层的polling（池化），原图像变为原来的1/4，故有image_size//4

各函数作用：ConvNet定义卷积神经网络；forward完成前馈神经网络运算；retrieve_features存储特征图

2.2  运行模型

net=ConvNet()  #此时会调用__init__()函数
criterion=nn.CrossEntropyLoss()   #交叉熵损失函数
optimizer=optim.SGD(net.parameters(),lr=0.001,momentum=0.9)
record=[]   #记录准确率等数值
weights=[]   #每若干步就记录一次卷积核
for epoch in range(num_epochs):   #循环周期设定为20次
    train_rights=[]     #记录训练集准确率
    '''下面的enumerate是构造一个枚举器的作用。就是我们在对train_loader做循环迭代的时候，
    enumerate会这个数字就被记录在了batch_idx之中，它就等于0，1，2，……
    train_loader每迭代一次，就会吐出来一对数据data和target，分别对应着一个batch中的手写数字'''
    for batch_idx,(data,target) in enumerate(train_loader):
        #Tensor转化为Variable，data为一批图像，target为一批标签
        data,target=Variable(data),Variable(target)
        net.train()       #打开dropout，防止过拟合
        
        output = net(data)  #神经网络完成一次前馈的计算过程，得到预测输出output
        
        #将output与target比较，计算误差，如标签是数字7，而通过net预测输出的output却是5，7与5之间存在误差
        loss=criterion(output,target)  
        optimizer.zero_grad() #清空梯度，因为Variable中requires_grad=True会默认累加梯度
        loss.backward()   #反向传播
        optimizer.step()    #一步随机梯度下降算法
        right=rightness(output,target)
        train_rights.append(right)
        
        if batch_idx %100 == 0:
            net.eval()
            val_rights=[]
            '''开始在校验数据集上做循环，计算校验集上面的准确度'''

            for (data,target)in validation_loader:
                data,target=data.clone().requires_grad_(),target.clone().detach()
                output=net(data)
                right=rightness(output,target)
                val_rights.append(right)
            #train_r[0]/trai_r[1]是训练集的分类准确度，另一个是校验集的
            train_r=(sum([tup[0] for tup in train_rights]),sum([tup[1] for tup in train_rights]))
            val_r=(sum([tup[0] for tup in val_rights]),sum([tup[1] for tup in val_rights]))
            print(val_r)
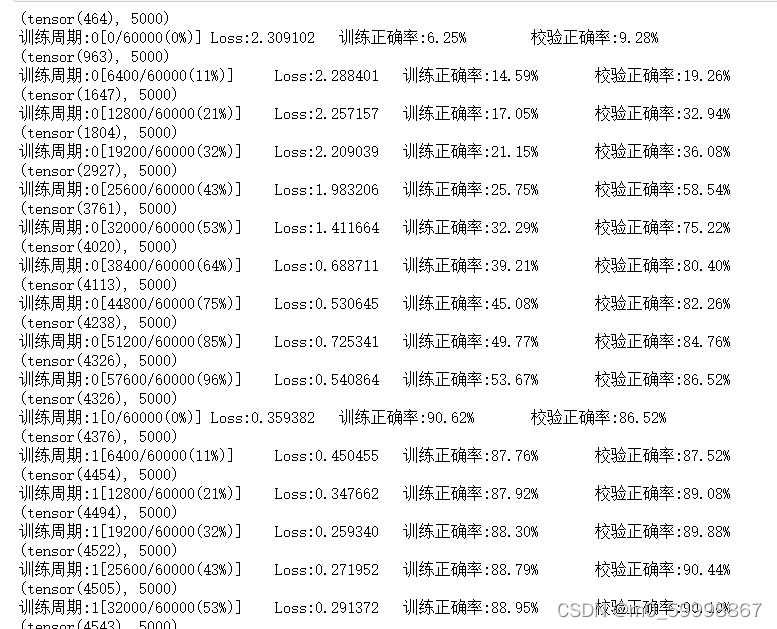
            print('训练周期:{}[{}/{}({:.0f}%)]\tLoss:{:.6f}\t训练正确率:{:.2f}%\t校验正确率:{:.2f}%'.format(
                  epoch,batch_idx * batch_size,len(train_loader.dataset),
                  100.*batch_idx/len(t。rain_loader),
                  loss.data,
                  100.*train_r[0].numpy()/train_r[1],
                  100.*val_r[0].numpy()/val_r[1]))
            #将准确率和权重等数值加载到容器中，方便后续处理
            record.append((100-100.*train_r[0]/train_r[1],100-100.*val_r[0]/val_r[1]))
            #weight记录了训练周期中所有卷积核的演化过程，net.conv1.weight提出了第一层卷积和的权重
            #clone备份weight.data中得到数据，否则weight.data变化时，列表中的每一项数据也会联动
            #所以这里使用clone函数十分重要
            weights.append([net.conv1.weight.data.clone(),net.conv1.bias.data.clone(),
                            net.conv2.weight.data.clone(),net.conv2.bias.data.clone()])
            

以下是部分训练结果截图：

 

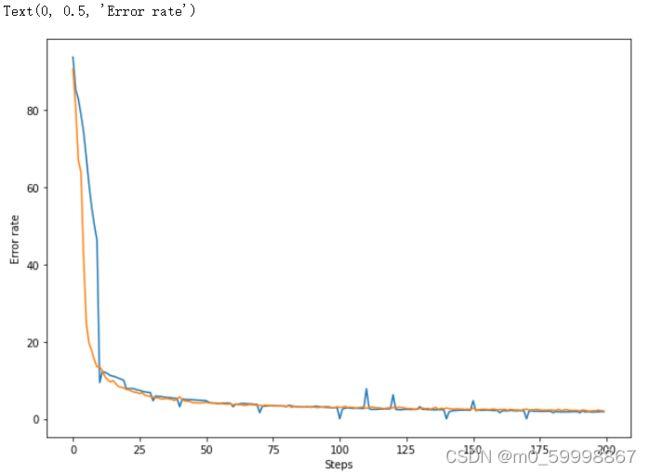
 绘制训练过程中的误差曲线

#绘制训练过程的误差曲线，校验集和测试集上的错误率
plt.figure(figsize=(10,7))
plt.plot(record)   #record记录了每一个打印周期记录的训练和校验数据集上的准确度
plt.xlabel('Steps')
plt.ylabel('Error rate')

结果如图：

2.3  在测试集上进行分类

#在测试集上分批运行，并计算总的正确率
net.eval()   #关闭dropout，标志模型当前为运行阶段
vals = [] #记录准确率

#对测试数据集进行循环
for data,target in test_loader:
    data.target = data.clone().detach().requires_grad_(True),target.clone().detach()
    output =net(data)  #将特征数据喂入网络，得到分类的输出
    val = rightness(output,target)   #获得正确样本数以及总样本数
    vals.append(val)   #记录结果

#计算准确率
rights = (sum([tup[0] for tup in vals]),sum([tup[1] for tup in vals]))
right_rate = 100.*rights[0].numpy() / rights[1]
print(right_rate)

#随便从测试集中读取一张图片，检验模型的分类结果，并绘制出来
idx = 2000
muteimg = test_dataset[idx][0].numpy()  
plt.imshow(muteimg[0,...])   #test_dataset的每一个数据由data和target组成，其中data为像素点矩阵，target为该图像标签数字
print('标签是：',test_dataset[idx][1])
print(test_dataset[idx])

#提取第一层卷积层的卷积核
plt.figure(figsize=(10,7))
for i in range(4):
    plt.subplot(1,4,i+1)
    plt.axis('off')    #关闭坐标轴
    plt.imshow(net.conv1.weight.data.numpy()[i,0,...]) 
    #第0个的第一行的所有数据为一个特征图，第1个的第一行的所有数据为第二个特征图，以此类推


#上面的卷积核我们不能够很好地解读，因此将其对应的特征图输出，便于理解
#先定义读入的图片，其中unsqueeze作用是在最前面添加一维
#目的是让input_x的tensor为四维，才能输入给net，添加的维是batch那一维
input_x = test_dataset[idx][0].unsqueeze(0)
#features是有两个元素的列表，分别表示第一层和第二层的所有特征图
feature_maps = net.retrieve_features(Variable(input_x))
plt.figure(figsize=(10,7))
 
#打印出4个特征图
for i in range(4):
    plt.subplot(1,4,i+1)
    plt.imshow(feature_maps[0][0,i,...].data.numpy())

2.4  滤波器（卷积核）的演化过程

#将记录在容器中的卷积核权重历史演化数据打印出来
i = 0
#tup是tuple元组的意思
for tup in weights:
    if i % 10 ==0:
        layer1 = tup[0]
        fig = plt.figure(figsize=(10,7))
        for j in range(4):
            plt.subplot(1,4,j+1)
            plt.axis('off')
            plt.imshow(layer1.numpy()[j,0,...])
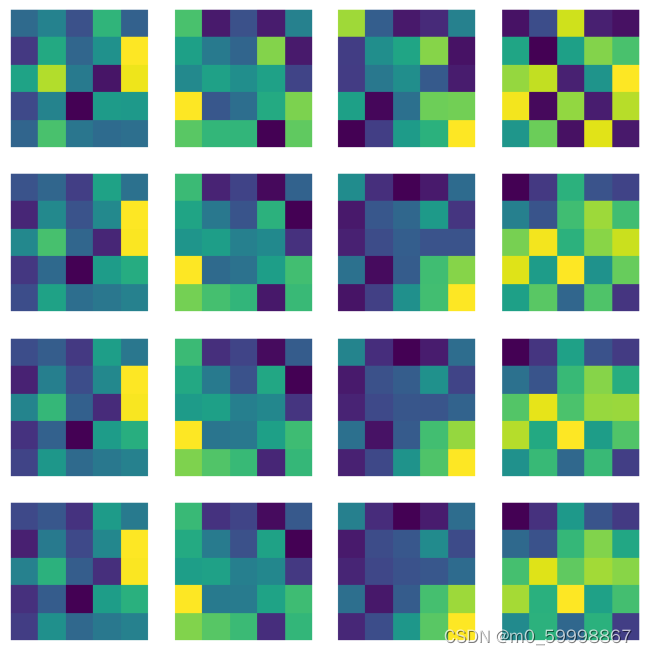
    i +=1

部分结果如图所示：

        由上图，我们可以看到，卷积核的演化过程共有4列，即以第一行的四个特征图为首，
依次不断地往下演化，即每一列对应一个卷积核 。

 

   【绘制第二层卷积核】

#绘制第二次的卷积核，每一列对应一个卷积核，一共8个卷积核（人为设定的4,8两个层的卷积厚度）
plt.figure(figsize=(15,10))
for i in range(4):
    for j in range(8):
        plt.subplot(4,8,i*8+j+1)
        plt.axis('off')
        plt.imshow(net.conv2.weight.data.numpy()[j,i,...])

#绘制第二层的特征图，一共八个
plt.figure(figsize=(10,7))
for i in range(8):
    plt.subplot(2,4,i+1)
    plt.axis('off')
    plt.imshow(feature_maps[1][0,i,...].data.numpy())

 

结论：从上述图像看出，图像的抽象程度变得更高了。由于池化的作用，即对图像进行模糊处理，  
一些多余的图像信息被丢弃了，这也证明了卷积网络的抽象提取能力 

2.5  卷积神经网络的健壮性

所谓健壮性，就是模型消除局部相关性的能力。即数字在图像平移后，模型是否仍能很好地正确预测出该数字

#随机挑选一张图片，把它往左平移w个单位，然后考察分类结果是否有变化

#提取test_dataset中第idx个批次第0个图像第0个通道对应的图像，定义为c
#原图像即为28*28， 因为这个是单通道图像
'''test_data[idx][0]的维度是（1,28,28）,即1个28行28列的矩阵，当我们
   取第1个时，即test_dataset[idx][0][0],可得到28行28列的二维张量'''
c = test_dataset[idx][0][0]   #shape为28*28

d = torch.zeros(c.size())  #全0的28×28的矩阵
w = 3  #平移的长度为3个像素



#对于d中的任意像素i，j  ，等于c中的i，j+w位置的像素（即d为c向左平移后的位置）
for i in range(c.size()[0]):
    for j in range(0,c.size()[1]-w):
        d[i,j] = c[i,j+w]

feature_maps = net.retrieve_features(Variable(c.unsqueeze(0).unsqueeze(0)))  #
plt.figure(figsize=(10,7))
 
#打印出4个特征图
for i in range(4):
    plt.subplot(1,4,i+1)
    plt.imshow(feature_maps[0][0,i,...].data.numpy())


#将d输入神经网络，得到分类结果pred，并打印
prediction = net(d.unsqueeze(0).unsqueeze(0))

''' torch.max(input, dim, keepdim=False, out=None) -> (Tensor, LongTensor)
    按维度dim 返回最大值，并且返回索引'''
pred = torch.max(prediction.data,1)[1]  #[1]即返回最大值对应的索引
print(pred)

#提取d对应的features特征图结果
feature_maps = net.retrieve_features(Variable(d.unsqueeze(0).unsqueeze(0)))  

plt.figure(figsize=(10,7))
#打印出4个特征图
for i in range(4):
    plt.subplot(1,4,i+1)
    plt.imshow(feature_maps[0][0,i,...].data.numpy())
    
plt.figure(figsize=(10,7))
for i in range(8):
    plt.subplot(2,4,i+1)
    plt.imshow(feature_maps[1][0,i,...].data.numpy())

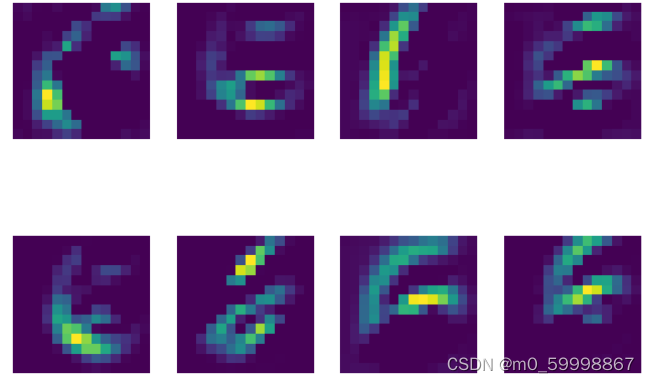
结论：平移数字输入后得到第二层特征图 。首先，网络打印出来的结果是6，说明我们的模型训练得能正确得预测出输入的数字，  并且对3个像素点的平移具有很好干抗干扰性，体现出卷积神经网络很强的健壮性。