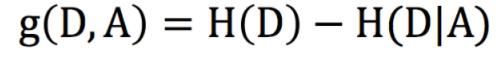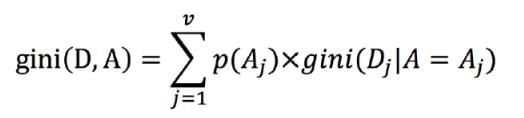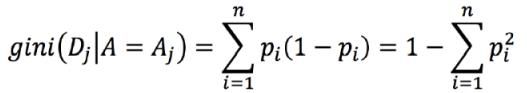决策树算法及其实现

决策树算法及其实现

1 什么是决策树

决策树（Decision Tree）是一种基本的分类与回归方法，本文主要讨论分类决策树。决策树模型呈树形结构，在分类问题中，表示基于特征对数据进行分类的过程。它可以认为是if-then规则的集合。每个内部节点表示在属性上的一个测试，每个分支代表一个测试输出，每个叶节点代表一种类别。
决策树的优点：
1）可以自学习。在学习过程中不需要使用者了解过多的背景知识，只需要对训练数据进行较好的标注，就能进行学习。
2）决策树模型可读性好，具有描述性，有助于人工分析；
3）效率高，决策树只需要一次构建，就可以反复使用，每一次预测的最大计算次数不超过决策树的深度。

决策树是我学过的最流行、最强大的机器学习算法之一。它是一种非参数监督学习方法，可用于分类和回归任务。目标是创建一个模型，通过学习从数据特征中推断出的简单决策规则来预测目标变量的值。对于分类模型，目标值本质上是离散的，而对于回归模型，目标值是连续的。与诸如神经网络之类的黑盒算法不同，决策树更容易理解，因为它共享内部决策逻辑(您将在下一节中找到详细信息)。

尽管许多数据科学家认为它是一种古老的方法,他们可能有一些怀疑它的准确性由于过度拟合问题,最近基于树模型,例如,随机森林(装袋方法),梯度增加(提高方法)和XGBoost(提高方法)是建立在决策树算法。因此，决策树背后的概念和算法非常值得理解!

2 算法原理

概述：决策树是离散数学的一种树型表示，可以表示离散函数。相较于KNN，PLA 等分类算法，其明显的特点是决策的结果可解释性很强。决策树是实现分治策略的数据结构，通过把实例从根节点排列到某个叶子节点来分类实例，可用于分类和回归。
决策树组成：决策树是一种用于对样本进行分类的树形结构。决策树由节点和边组成。节点类型有两种：内部节点个叶子节点。内部节点属于一个特征，节点的分支根据特征的取值来分支；叶子节点即为样本的一个分类。
决策树分类过程：决策树决策是基于树结构来进行决策的，类似与人脑在面临决策问题时一种自然的处理机制：依次判定一个决策问题的属性，到最后得出问题的结论。例如，判断一个西瓜是否为好瓜是，首先判断这个西瓜的颜色，如果颜色为深绿，再来看西瓜的纹理，然后看西瓜的软硬程度。。。最后得出这个西瓜是好的还是坏的。依据节点纯度选择最优划分属性：在决策树的建树过程中，需要对数据不断划分。一般而言，决策树的分支节点所包含的样本尽可能属于同一个类别，即节点纯度越高越好。在信息论中，期望信息越小，那么信息增益就越大，从而纯度就越高。划分最优属性的方法有ID3信息增益，C4_5 信息增益率，CART 基尼指数；

ID3(信息增益）：ID3 是通过选择信息增益最大的属性来提高节点的纯度。

• 信息熵：为离散随机事件出现的概率，信息熵越高，系统越有序；信息熵越低，系统越混乱。一个属性的变化情况越多，它携带的信息量就越大。假定d 数据的类别，数据D的信息熵定义为：

• 条件熵：条件熵是数据集在特征A 的情况下的信息熵，其定义如下：

• 信息增益：信息增益越大，意味着使用属性A 来划分所获得的纯度提升越大，因此选择属性时，选择信息增益最大的属性。信息增益定义如下：

C4_5(增益率)：

信息增益（ID3）对可取值数目较多的属性有所偏好，假如这个属性每一个分支只有一个样本，这些分支结点纯度已经达到最大。然而这种决策树往往导致过拟合，为减少ID3 这种偏好带来的不利影响，使用增益率来选择最优划分属性。

• 增益率定义：
• 

其中SplitInfo(D,A)是在特征A 的情况下数据集D 的熵：

CART(基尼指数):

基尼指数反映了数据集D 中随机抽取两个样本，其类别不一致的概率。基尼指数越小，不确定越小，数据集的纯度越高。

• 基尼指数定义

其中：

3 剪枝处理

决策树考虑了所有数据点而生成的树，因此决策树一个明显的缺点是容易生成过于复杂的树而导致过拟合。一个防止过拟合的方法是剪枝处理，通过剪枝处理降低决策树的复杂度，降低过拟合的概率。

• 预剪枝：在决策树生成过程中对每一个结点进行估计，若当前结点的划分不能带来决策树泛化性能的提高，则将该结点标记为叶结点。
• 后剪枝：先生成一个完整的决策数，然后对所有非叶结点进行考察，若将该结点对应的子树替换为叶结点可以提高树的泛化性能，则替换为叶子结点。

4 伪代码

Input:训练集D
属性集A
Output：以root 为根节点的决策树
Process：函数TreeGenerate(D,A)
1: 生成节点node；
2: if D 中的样本属于同一类别C then
3： 将root 标记为C 类叶节点； return
4: end if
5: if A 为空集，或D 中所有样本在A 中所有特征上取值相同
6： 将root 标记为叶节点，类别标记为D 中中样本数最多的类： return
7: end if
8： 遍历当前节点数据集和特征，根据某种原则，选择一个特征a
9： for a 中的每一个值a_value do
10：根据a_value 的取值，得到D 中在a 上取值为a_value 的样本子集Di
11：为node 生成一个分支
12：if Di 为空then
13： 将子节点标记为叶节点，类别为父节点中出现最多的类； return
14：else
15： 以TreeGrnreate（Di，A\{a}）为分支节点。
16: end if
17: end for

5 决策树实现

5.1 使用sckit-learn机器学习算法包来实现男女的类别划分

sckit-learn中的 sklearn.tree.DecisionTreeClassifier¶函数详解：https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html

首先将数据读入，并且提取出排序的三个特征，和样本的标签

path = '../作业数据_2021合成.xls'
data = pd.read_excel(path)  # 读入的数据结构为dataframe类型
data = data[['喜欢颜色','喜欢运动', '喜欢文学', '性别 男1女0']]
data.replace({'白':0,'黑':1,'紫':2,'绿':3,'蓝':4,'黄':5,'橙':6,'灰':7,'红':8,
              '粉':9,'鹅黄':5,'蓝绿':4,'金':10,'青':11,'浅绿':3
              },inplace=True)

将数据集中的样本随机抽取，进行重新排序，抽取样本总量的70%来作为训练集，剩余的30%作为测试集

dataset = data.sample(frac=1)
train_len = dataset.shape[0] * 0.7

train_set = dataset.values[:int(train_len), :]
train_label=train_set[:,-1]
train_set=train_set[:,:-1]

test_set=dataset.values[int(train_len):, :]
test_label=test_set[:,-1]
test_set=test_set[:,:-1]

实例化决策树类对象，并使用c4.5算法，对训练集进行训练，并生成决策树的dot文件。

clf = DecisionTreeClassifier(criterion='entropy')
clf.fit(train_set, train_label)
dot_data = tree.export_graphviz(clf, out_file=None,
                         feature_names=['like color','like sports','like literature'],
                         class_names=['man','faman'],
                         filled=True, rounded=True,
                         special_characters=True)

将生成的决策树保存到pdf文件中

graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("iris.pdf")

接下来使用测试集，对训练好的决策树进行验证，使用先前分好的测试集。

pridict_label=clf.predict(test_set)

将测试集输入决策树进行分类，并且返回分类标签。

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1
 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1
 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1]

打印，测试集样本原先的标签，统计分类准确率。

[0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 1 1
 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1
 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1]

tp = 0
tn = 0
fp = 0
fn = 0
for i in range(0, len(pridict_label)):
    if pridict_label[i] == test_label[i]:
        if pridict_label[i] == 1:
            tp = tp + 1
        else:
            tn = tn + 1
    else:
        if pridict_label[i] == 1:
            fp = fp + 1
        else:
            fn = fn + 1
print(pridict_label)
print('实际为1预测为1的样本个数TP=', tp)
print('实际为1预测为0的样本个数FN=', fn)
print('实际为0预测为1的样本个数FP=', fp)
print('实际为0预测为0的样本个数TN=', tn)
print('样本总数', len(pridict_label))

统计预测正确和错误的样本个数，打印结果如下：

实际为1预测为1的样本个数TP= 84
实际为1预测为0的样本个数FN= 4
实际为0预测为1的样本个数FP= 14
实际为0预测为0的样本个数TN= 4
样本总数 106

列表如下：

	预测1	预测0	合计
实际1	TP=84	FN=4	88
实际0	FP=14	TN=4	18
合计	98	8	106

接下来计算模型性能指标
$$SE=\frac{TP}{TP+FN}=\frac{84}{84+4}=95.5\%$$

$$SP=\frac{TN}{TN+FP}=\frac{4}{4+14}=22.2\%$$

$$ACC=\frac{TP+TN}{TP+FP+FN+TN}=\frac{88}{106}=83\%$$

5.2 使用python实现决策树

导入excel数据，并提取数据，前三列为属性，最后一列为label。

import pandas as pd

path = '../作业数据_2021合成.xls'
data = pd.read_excel(path)  # 读入的数据结构为dataframe类型
data = data[['喜欢颜色', '喜欢运动', '喜欢文学', '性别 男1女0']]

喜欢颜色  喜欢运动  喜欢文学  性别 男1女0
0      蓝     1     1        1
1      蓝     0     0        1
2      蓝     1     0        1
3      绿     0     1        1
4      蓝     0     0        1
..   ...   ...   ...      ...
346    蓝     0     0        1
347    白     0     0        1
348    黄     1     0        1
349    橙     1     0        1
350    白     1     0        1

[351 rows x 4 columns]

将label的名字提取出来并打印

t = data.keys()[-1]
print('Target Attribute is   ➡ ', t)

Target Attribute is   ➡  性别 男1女0

获取用于分类的属性名称list，并且移除label的名称

# Get the attribute names from input dataset
attribute_names = list(data.keys())
# Remove the target attribute from the attribute names list
attribute_names.remove(t)
print('Predicting Attributes ➡ ', attribute_names)

定义计算信息熵的函数，入口参数probs为一个列表，第k个元素是第k类样本所占的比例$ p_k $。

# Function to calculate the entropy of probaility of observations
# -p*log2*p
#Entropy of the Training Data Set
def ent(y): # OK
    p = np.array([np.count_nonzero(y==i)/y.size for i in np.unique(y)])
    return -p@np.log2(p)

定义计算信息增益的函数，

# Function to calulate the entropy of the given Datasets/List with respect to target attributes
#X:输入的数据集
#y:属性列表
#a:第a列，就是第a个特征

def gain(X, y, a, continuous): # OK
    """Possible issue: attributes.size <= 1?
    """
    attributes = np.unique(X[:,a])
    if not continuous:
        y_new = [ y[X[:,a]==i] for i in attributes]
        result = ent(y) - sum(i.size*ent(i) for i in y_new)/y.size
        return (result, None)
    else:
        if attributes.size <= 1:
            return (-1, None) # should never be chosen
        result = 0
        split_point = (attributes[0]+attributes[1])/2
        for i in range(attributes.size-1):
            current_split_point = (attributes[i]+attributes[i+1])/2
            y1 = y[X[:,a]<=current_split_point]
            y2 = y[X[:,a]>current_split_point]
            current_gain = ent(y)-(y1.size*ent(y1)+y2.size*ent(y2))/y.size
            if current_gain > result:
                result = current_gain
                split_point = current_split_point
        return (result, split_point)