【数据结构C语言版本】邻接矩阵邻接表的创建与输出(附完整代码)
目录
-
- 写在前面但是现在不想写
-
- 此篇推荐《Wonderful Tonight》by Babyface,岸部的同名指弹也十分温柔
- 1.邻接矩阵
-
- 1.1. 存储结构
- 1.2.功能实现
-
- 1.2.1 图的创建
- 1.2.2 打印比创建难你会信?
- 1.2.3.完整代码实现
- 1.2.4.测试结果
- 2.邻接表
-
- 2.1. 理解存储结构才是最难的
- 2.2.功能实现
-
- 2.2.1 创建
- 2.2.2 打印
- 2.2.3.完整代码实现
- 2.2.4.测试结果
写在前面但是现在不想写
此篇推荐《Wonderful Tonight》by Babyface,岸部的同名指弹也十分温柔
辛丑年冬月初一,微冷,键盘不如砚冰坚,手指尚能屈伸,但仍旧敲不出只有五行算法的Floyd,自修室确实好睡,周杰伦唱《雨下一整晚》,周树皮能口水流一整页,也算是身体的一部分和算法融为一体了,课设是不敢稍逾约,计了计日还有12天,还是好好加油,以中有足乐者,无惧算法水平不若人也。
附上一段《大话数据结构》图章节结语(节选)
“世界上最遥远的距离,不是牛A与牛C之间的狭小空隙,而是你们当中,有人在通往牛X的路上一路狂奔,而有人步入大学就学会了放弃!”
1.邻接矩阵
图由两部分构成:1.顶点数组 2.边关系。故我们需要定义两个独立的存储结构分别存储这两个关系。
1)先从顶点数组说起,顶点数组不分大小主次,故可用一个一维数组存储顶点信息。
2)对于边与边之间的关系,我们可以模仿球队赛程表,运用二维数组,借助行列之间的关系来存储某两边之间的关系。
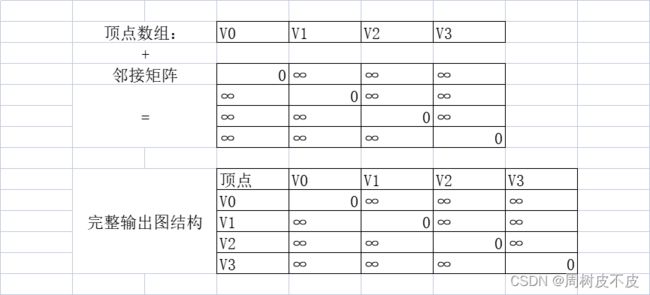
因为是对数组的操作,所以我们的下标是从0开始,也就意味着我们后续对邻接矩阵进行赋值等操作时还需要将下标-1,这无疑不符合程序人性化的设定,如何解决邻接矩阵从下标(1,1)开始存储关系的问题呢?
我们不妨先将第0行和第0列的全部存储空间浪费,从第1行第1列开始存储元素,到顶点总数行顶点总数列结束存储,如此便解决了人脑预想存储位置与计算机存储位置不符的问题。
再看浪费的存储单元,我们可将顶点信息赋值给第0行的第1个元素到第numnodes个元素与第0列第1个元素到第numnodes个元素,作为输出时的表头,如此不仅将原浪费的存储空间充分利用,还增强了程序输出时的可读性。
1.1. 存储结构
到这里相信读者应该能很快定义出图的四个重要元素之二:顶点数组(一维)与邻接表(二维)。
初次之外,对于顶点表,我们还需要一个numNodes用于记录顶点个数;以及numEdges记录边条数。
因此,我们可定义出如下图的结构
typedef char VertexType; //顶点类型应由用户定义
typedef int EdgeType; //边上的权值类型应由用户定义
//定义邻接矩阵存储结构
typedef struct MGraph{
int numNodes; //用于记录顶点个数
int numEdges; //用于记录边个数
VertexType vexs[MAXSIZE]; //用于保存顶点元素
EdgeType arcs[MAXSIZE][MAXSIZE];//用于保存边元素
}MGraph;
1.2.功能实现
1.2.1 图的创建
- 顶点数组初始化表头
由之前的描述可知,输出图矩阵的第0行的第1个元素到第numnodes个元素与第0列第1个元素到第numnodes个元素都依次由顶底信息赋值。
故我们的操作为:
(1)用户自定义输出顶点信息
(2)初始化表头信息,将(0,0)赋值为-1,方便后续判断输出
(3)利用for循环,将顶点信息赋值给输出图矩阵
//初始化顶点数组信息
printf("输入顶点信息(格式为A(空格)B(空格)C):\n");
for(i = 0;i <(*G)->numNodes;i++){
scanf(" %c",&(*G)->vexs[i]);
}
//表头初始化
(*G)->arcs[0][0]=-1;
for(k=1;k<=(*G)->numNodes;k++){
(*G)->arcs[0][k]=k;
(*G)->arcs[k][0]=k;
}
- 初始化邻接矩阵
case1:对角线元素
此时边关系为顶点自身间的距离,我们将其权重赋值为0
case2:其他元素
此时边关系为两顶点间的距离,初始化时我们将其权重暂且赋值为∞
//整表初始化∞0
for(i = 1;i <=(*G)->numNodes;i++){
for(j =1;j<=(*G)->numNodes;j++){
if(i==j){
(*G)->arcs[i][j]= 0; //与自己的距离
}
else (*G)->arcs[i][j]= GraphINF;
}
}
- 边结点的赋值
用户自定义输入权重并赋值,因是无向图,故需将对称元素同时赋值。
//连接有权重边的结点的赋值
for(k = 1;k <=(*G)->numEdges;k++) //读入numEdges条边,建立邻接矩阵
{
printf("输入边(vi,vj)上的下标i,下标j和权w(格式为i,j,w):\n");
scanf("%d,%d,%d",&i,&j,&w); //输入边(vi,vj)上的权w
(*G)->arcs[i][j]=w;
(*G)->arcs[j][i]= (*G)->arcs[i][j]; //无向图
}
1.2.2 打印比创建难你会信?
首先需明确数组中存储的为边之间的权重
case1:权重为GraphINF
输出“∞”
case2:权重为-1
之前初始化时将(0,0)赋值为-1,输出“顶点”
case3:为第0行或是第0列
利用顶点数组,输出“顶点信息”
case4:其他
剩下的为边与边之间的权重,输出“对应权重”
for(i=0;i<=G->numNodes;i++){
cnt=1;
for(j=0;j<=G->numNodes;j++){
if(G->arcs[i][j]==GraphINF){
printf(" ∞");
}
else if (G->arcs[i][j]==-1){
printf("顶点");
}
else if(i==0&&j!=0){
elem=(int)(G->vexs[j-1]);
G->arcs[0][j]=elem;
printf(" %c ",G->arcs[0][j]);
}
else if(i!=0&&j==0){
elem=(int)(G->vexs[i-1]);
G->arcs[i][0]=elem;
printf(" %c ",G->arcs[i][0]);
}
else printf(" %d ",G->arcs[i][j]);
if(cnt%(G->numNodes+1)==0){
printf("\n");
}
cnt++;
}
}
1.2.3.完整代码实现
#include 1.2.4.测试结果
2.邻接表
当我们存储边数较少的稀疏图时,若仍用邻接矩阵存储,无疑是浪费的大片的存储空间。类比当年我们用链栈解决顺序栈存储空间浪费的问题,我们也可通过链表存储边的关系。
于是乎,我们将数组存储顶点表(方便查找),链表存储边关系的存储方法称为邻接表。

2.1. 理解存储结构才是最难的
(1)边表结点(链表)

因为存在边数占总边数比例的不确定性,我们是有链表结构来存储边表结点,因此我们需要一个指向下一个邻接结点的指针(next),此外我们还需记录该邻接结点的信息:结点下标(adjvex)与权重(weight)
代码实现如下:
//边表结点结构
typedef struct EdgeNode{
int adjvex; //用于存储边表的下标
EdgeType weight; //用于存储边表权值
struct EdgeNode *next; //用于指向下一个邻接点(边表结点)
}EdgeNode;
(2)顶点(一维数组)

顶点的作用其实就是方便我们查找图中某个点的边关系,所以需要一个指针(firstedge)指向其的第一个邻接结点,之后的邻接结点间因有next指针连接,故我们可查询顶点连接所以邻接结点的信息。
如,当我们想查询(i,j)间是否存在边关系时,只需要找到顶点边中的Vi,看Vi指向(firstedge)的第一个邻接结点的下标(adjvex)是否为j即可。
打印路径也是,只要该顶点仍存在边表结点,则通过该边表结点下标找到其对应的顶点信息并打印,此部分会在功能函数打印中详述。
//顶点结构
typedef struct VertexNode{
VertexType data; //用于存储顶点结点信息
EdgeNode* firstedge; //用于存储第一个邻接点
}VertexNode,AdjList[MAXVEX];//定义AdjList[MAXVEX]为顶点数组
(3)邻接表(顶点数组+边表链表)
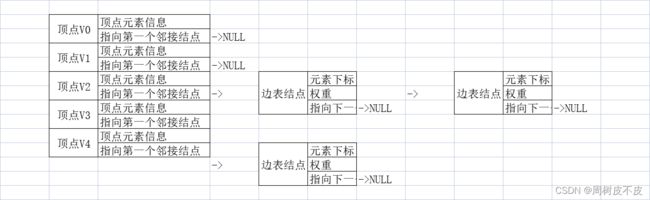
根据前面的讲解,我们能很轻易得定义出一个顶点表类型的一维数组(adjList)用于存储每个顶点的信息,除此之外我们需定义numNodes用于记录顶点个数,定义numEdges用于记录边的条数。
此时需注意,因为邻接结点存储结构是链表的形式,且我们能通过顶点的指针域(firstedge)以及边表结点间的指针域(next)找到所以边表结点,故在邻接表中不需要定义邻接结点的结构。
//邻接表结构
typedef struct ALGraph{
int numNodes; //用于记录顶点个数
int numEdges; //用于记录边个数
AdjList adjList; //用于存储顶点的数组
//VertexNode adjList[MAXVEX]; 顶点数组这样也ok
}ALGraph;
2.2.功能实现
2.2.1 创建
- 初始化顶点表
(1)用户自定义输入顶点数目(numNodes)与边数目(numEdges)
printf("请输入顶点数与边数(格式为i,j):\n");
scanf("%d,%d",&(*G)->numNodes,&(*G)->numEdges);
(2)初始化顶点表信息,并将顶点表指向第一个邻接结点的指针域置空
//初始化顶点表
for(i=0;i<(*G)->numNodes;i++){
scanf(" %c",&((*G)->adjList[i].data)); //输入顶点表信息 %c前空格吃回车
(*G)->adjList[i].firstedge=NULL; //将顶点表的邻接点指针域置空
}
(3)自定义输入边关系
for(k=0;k<(*G)->numEdges;k++){
printf("请输入i->j的两个顶点(格式:A(空格)C):\n");
scanf(" %c %c",&v1,&v2);
//获取邻接点的data
i=LocateVex((*G),v1);
j=LocateVex((*G),v2);
- 建立邻接表间的逻辑关系
(1)获取目标结点下标(LocateVex函数)
首先需明确一个概念:顶点V0,V1,V2,V3的顶点信息(data)存储的是A、B、C、D, 而当这些顶点被当成邻接结点时进行存储时,存储的便是其邻接结点下标(adjvex)1、2、3、4,其实也就是其位于顶点表中的下标。
故我们在这里定义一个Locate函数,1)通过A、B、C、D的顶点信息(data)遍历顶点数组,2)找到对应字符位于顶点数组的位置下标(index)1、2、3、4,3)并将值返回给边表结点的下标(adjvex),以进行后续的头插法与打印操作。
NodeReturnType LocateVex(ALGraph *G,char vex)
{
int index;
for(index=0;index<G->numNodes;index++){
if(G->adjList[index].data==vex){
return index;
}
}
}
(2)头插法

Step1 新结点:
1)数据域:Locate函数返回值赋值新结点下标(adjvex)
2)指针域新结点的下一个邻接结点(next)指针域指向邻接
Step2 原邻接结点:
1)指针域:指向空
Step3 顶点数组:
1)指针域:第一个邻接结点指针(firstedge)指向新结点
//头插法 无向图所以两个顶点都需要操作
//i->j
NewarcNode1=(EdgeNode*)malloc(sizeof(EdgeNode)) ;
NewarcNode1->adjvex=i;
NewarcNode1->next=(*G)->adjList[j].firstedge;
(*G)->adjList[j].firstedge=NewarcNode1;
//j->i
NewarcNode2=(EdgeNode*)malloc(sizeof(EdgeNode)) ;
NewarcNode2->adjvex=j;
NewarcNode2->next=(*G)->adjList[i].firstedge;
(*G)->adjList[i].firstedge=NewarcNode2;
2.2.2 打印
输出样式 Vex:Edge1 Edge2…
对于顶点表中每个结点的操作相同,首先输出顶点表的数据信息,接着通过firstedge指针与next指针,运用p=p->next(p为当前结点)遍历该顶点数组的所有边表结点并打印,直到没有为止(p==NULL)
//打印邻接表
void PrintALGraph(ALGraph *G)
{
int i,j;
EdgeNode *p; //用于指向当前操作边结点
// 输出顶点结点
for(i=0;i<G->numNodes;i++){
printf("顶点%c",G->adjList[i].data) ;//注意是%c
// printf("numNodes=%d",G->numNodes);
for(p= G->adjList[i].firstedge;p!=NULL;p=p->next){
printf("->%d ",p->adjvex);
}
printf("\n");
}
printf("\n");
}
2.2.3.完整代码实现
#include
