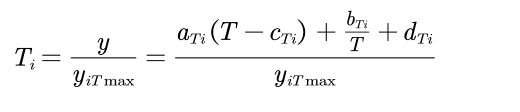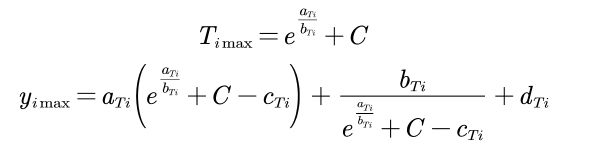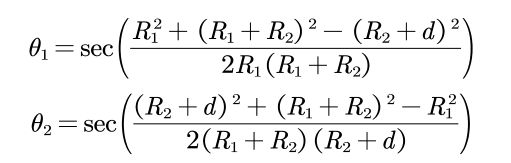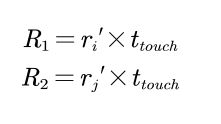2021美赛A题元胞自动机解法(M奖)
距离比赛已经整整一年了,今天突然想整理一下以前比赛的代码,所以下面是回忆着写的,可能有错误的地方,欢迎大家指正。
主要是建了下面3个模型,一一说明:
Model I
首先要建立多种真菌存在下的分解速率模型,这里我是考虑到单个菌落的分解速度以及菌落之间的竞争作用。这里多种菌落分为强弱菌种,建立的模型中强菌会逐渐覆盖掉弱菌。而决定菌种生长速度的,则是耐湿性和分解速率(根据题意)。然后我将真菌的相互作用分为了3个阶段:无影响、干扰和寄生,具体原因可见后面的reference。每个阶段都有对应的解析式,并且我用了一个几何模型来表示真菌之间的扩散作用。然后是大气趋势变化,这里给出了相互作用的短期和长期趋势。
Model II
这里结合Model I给各种菌做了ranking 然后给出了一些影响ranking的指标,全部是结合文献而来。
Model III
这里用元胞自动机做的生态系统仿真,时间原因只用了2种菌仿真,主要是多种菌的代码由于状态转换问题求补集容易有bug,当时没时间调了。并且也用元胞自动机做了Sensitivity Analysis 。
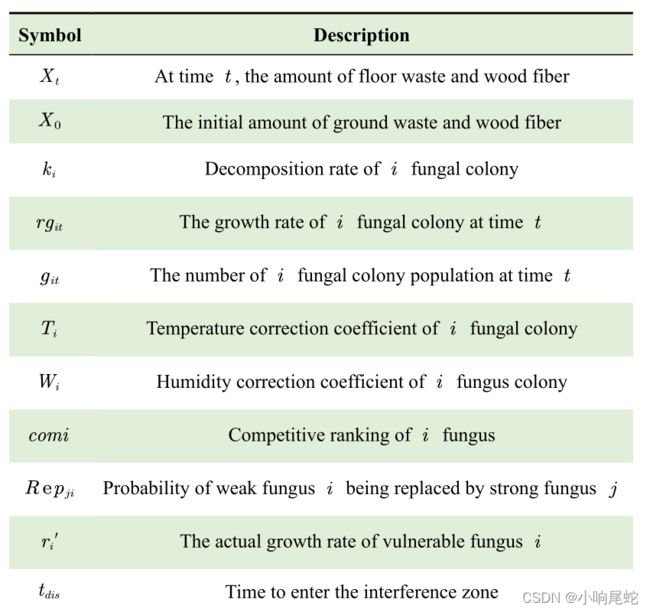
先上摘要和符合说明
The carbon cycle is a significant part of the Earth’s biosphere activities. The
degradation of wood littered by fungi plays a key role in the carbon cycle. Based
on the idea of differential equation and computer simulation, three models were
established by studying fungi and their growth environment, which was helpful to
understand the key parts of carbon cycle.
Model I, A dynamic decomposition model of the interaction of various strong
and weak fungi with environmental impact: we took the growth rate of fungi and
its moisture tolerance as the main factors affecting the decomposition rate. Based
on this, a mathematical representation of the decomposition process of the colony
was constructed. This paper found that the interaction between fungi includes three
stages of non-influence, interference, and parasitism. Then the mathematical
expression of the decomposition rate in each stage was derived. And the dynamic
interaction of any two fungi was shown in a geometric way. The results showed
that the competition between the colonies will not be conducive to the decompo-
sition of both parties. The influence mechanism of atmospheric trend changes on
the interaction was shown. The results showed the short-term and long-term trends
of the interaction between fungi.
Model II, A prediction model of the advantages and disadvantages of fungal
species considering environmental factors: the competition ranking of fungi in
the same environment was quantified. The projection of each fungus on the main
components of the competition ranking was used to quantify their competitive
ability. Then we predicted the influence of other environmental components on the
advantages and disadvantages of each fungus. We used data from Alaska to Puerto
Rico. The data can reflect the adaptability of fungi to different environments. Then
the optimal value of each fungus in each environment from the three aspects of
temperature, humidity, and PH was given. We gave the basis to judge the relative
advantages and disadvantages of each kind of fungi. Finally, data from the refer-
ence was used to obtain the optimum values. The values were about temperature
and humidity for each fungus in different environments, then each fungi’s ad-
vantages and disadvantages could be judged.
Model III, A prediction model for the diversity and importance of fungal com-
munities: we analyzed the mechanism of the decomposition of ground waste and
wood fiber by the fungal community system with biological diversity. Then the
mathematical expression of the system decomposition rate was built. The cellular
automata was used to simulate the evolution process of the system with relatively
high and low biodiversity. The Specific value was given under the impact of the
environment on the three aspects of Model II. Among them, the average value of
system deviations with high population abundance was 27%, and the average value
of system deviations with low population abundance was 29%.
分解率定义
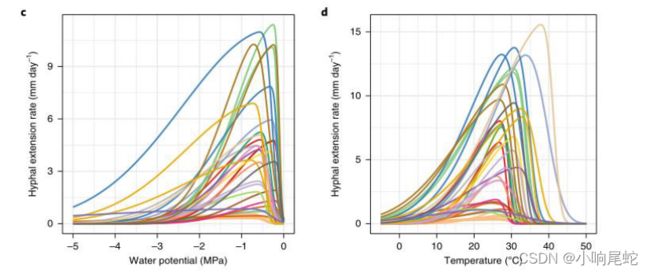
地面废弃物和木材纤维上真菌的分解速度主要与真菌的两个特性有关: 真菌的生长速度和真菌的抗湿性。因此,主要研究这两个特性,以建立多种真菌存在时的分解模型。最后,确定了两者之间的关系如下: 地面废弃物和木材纤维上的真菌的分解速度取决于菌丝的延伸速度和真菌的抗湿性。菌丝体的扩展速度实质上是真菌的生长速度 ,它是由大气环境的温度和湿度决定的,如下图所示。
要研究真菌对地面废弃物和木材纤维的分解速率,必须考虑外界环境因素和真菌系统内部的相互作用。为了简化模型,我们首先忽略了真菌之间的相互作用。在外界环境的作用下,每一种群体都有其最佳的生存环境,包括温度和湿度。因此,仅考虑外部环境,地面废弃物和木材纤维的分解是由多种真菌在特定温度和湿度下的所有单菌落分解地面废弃物和木材纤维的简单合成。因此,该问题可以简化为研究在特定的外部条件下,单个菌落分解地面废弃物和木材纤维的问题。
对于一个菌落,其地面废弃物和木材纤维的分解遵循一个指数动态规律如下
![]()

如前所述,真菌在地面废弃物和木材纤维上的分解速率取决于菌丝的延伸速率和菌丝的耐湿性,而菌丝的延伸速率取决于大气环境的温度和湿度。因此,应该有以下的形式
![]()

然后下面是结合的组织增长模型,因为菌种的规模越大生长速率就越慢,这里就用logistic了,得到下面的规律:
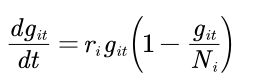
用matlab求解,可以求得该式的解析解:

这样就可以得到某种菌的生长速率,如上式左边与r的乘积
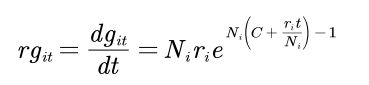
那么到这里其实就得到了生长率的解析式了。但是看这个式子,这里的函数还需要具体解释。
![]()
通过查阅文献资料,我们发现北美37种真菌菌丝伸长率与温度的关系如下图所示。研究了菌丝伸长率与湿度的关系,结果表明: 菌丝伸长率随湿度的增加而增加,随湿度的增加而增加。根据数据,这里要符合一个倒的对勾函数。
那么根据上面几个式子,就可得到
![]()
对于单菌落来说,分解木质纤维的速度满足:
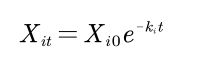
那么对于整个系统,整体的分解速率就是所有菌落的分解速度之和(不考虑相互作用时)
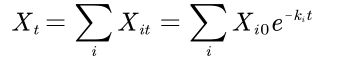
相互作用
这里定义了3个阶段,以两种菌落为例,有接触前,即将接触时,接触后,分别定义为
non-contact area, the interference area, and the parasitic area
![]()
该图显示了强真菌 j (绿色)侵入弱真菌 i (黄色)的过程。实际上,不同菌群相互接触后存在以下三种情况,强菌群侵入弱菌群的可能性较大,两个菌群处于死锁状态,弱菌群侵入强菌群的可能性较小,这里不考虑最后一种情况。
面积 G 和 D 分别代表深黄色和深绿色圆形区域中心,E 和 F 分别代表 D 面积以外的两层圆盘结构,H 面积代表 G 面积以外的圆盘。面积 D 代表强菌群形成的菌落半径,面积 G 代表弱菌群形成的菌落半径。
那么弱势真菌在强势真菌入侵时的生长区域则为
![]()
而表明强菌入侵结束后,强菌群的领地,被粉红线包围是
![]()
强菌入侵时强菌的生长区域则是
![]()
当入侵过程不发生时,表示弱势真菌在强势真菌入侵期间的生长面积。
所以下面就只剩一个当入侵过程发生时的生长速度,这里还是根据文献,提出了一个覆盖率的概念。
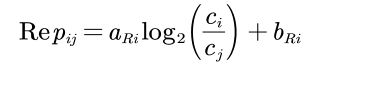
根据这个式子,可以表示上述图形中的各个参数,公式推导这里就不写了,直接写结果:
![]()
到目前为止,本文已经得到了关键参数的表达式和公式 ,可以把它们放入前面的分解率计算公式中,得到系统的分解速率。
这个模型我觉得比较合理的是,上面的各式正好可以得到一个比较漂亮的结果:
对于弱真菌,下面的公式适用于

而对于强真菌,下面的公式适用于

在菌落分解速率与菌落边缘周长成正比的前提下,可以得到物理中反映的规律:
这里 k i 3 k_{i3} ki3 和 k j 3 k_{j3} kj3代表寄生区较弱真菌和较强真菌的分解速度; k i 2 k_{i2} ki2 和 k j 2 k_{j2} kj2则代表干扰区弱、强真菌的分解速率。
正好是不考虑相互左右的分解率×了一个小于1的衰减系数(为什么小于1可以根据 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2的表达式证明),而对于强势菌,则加了一项与衰减量相同系统的增长系数,所以可以得到如下结论:
由于强菌进入寄生区后取代弱菌的速度比弱菌的膨胀速度慢得多,本文认为强菌在环境不发生干燥变化的情况下,不会完全取代弱菌,而是处于侵入与入侵并存的状态。由于弱势真菌有膨胀率,当强势真菌侵入弱势真菌时,侵入弱势真菌相应部位的强势真菌的生长速度低于强势真菌边缘其他部位的生长速度。
大气作用
这项并不是我认为模型中的精彩部分,就不多做叙述了,只放一张思路图

结合上面的部分,也可以得出解析式(运气好),正好是个双曲正切,但是有点复杂。
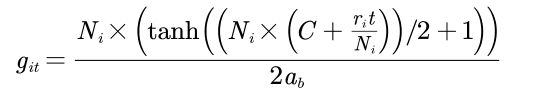
多菌落分解模型
首先分析了利用真菌群落多样性分解地表废弃物的机理,建立了以分段函数描述系统总体分解效率的数学表达式。然后利用元胞自动机模拟了生物多样性系统和非生物多样性系统在局部环境具有不同程度变异时的演化过程,给出了环境影响率的三个方面。
这里的分解率公式都是根据上面的模型建立的。
主要考虑了任意两个群体之间的相互作用,建立了一个动力学模型。在此基础上,我们继续研究了不同真菌菌落分解模型的形成,并探讨其对系统分解地面垃圾总效率的影响。
如果只有两种菌的情况下
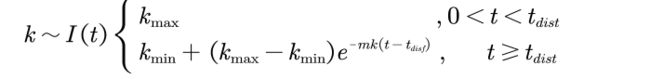
所以当系统中存在多种菌时,分解率随时间的变化如下图所示:
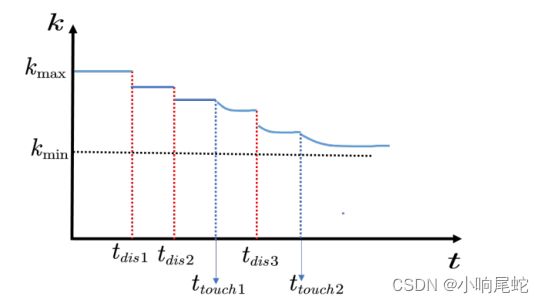
如果 t d i s i \ t_{disi} tdisi 的数量趋近与无穷,意味着系统中如果存在足够多个菌落,由上图可以轻易看出,整体系统的分解速率满足:
![]()
这与上面定义的单菌落的公式完全对应。
元胞自动机仿真
为了简化计算,本文将某一地区两种不同真菌的存在视为生物多样性,将某一地区一种真菌只有两个亚种的存在视为非生物多样性。为他们制定规则。本文讨论了环境波动对真菌群落的影响。主要表现在三个方面: 某种真菌停止生长和死亡,强真菌的置换率增加,弱真菌转化为强真菌。我们的工作是量化这三个方面的内容。当一个地区有两种不同的真菌时,在三种情况下,某种真菌的实际生长率下降50% ,其他真菌不变,弱真菌的实际生长率下降50% ,强真菌的实际生长率上升50% ,强真菌对弱真菌的覆盖率上升50% ,弱真菌直接被强真菌取代。当一个地区有一种真菌的两个亚种时,这三种情况分别对应两种真菌的实际生长率下降50% ,两种真菌的实际生长率下降50% ,没有影响。
让程序进入循环,使分解过程图像和变量变化过程图像。分解速率公式以概率的形式给出。具体规则是: 当细胞周围有 n 个代表木纤维的细胞,可以转化为代表真菌的细胞时,它就有转化的可能性N*P,其中 p 与真菌的分解速度相对应。值得注意的是,考虑到弱真菌在直接竞争中弱于强真菌,他们需要改进其他方面,以增加生存的可能性,所以我们让弱真菌比强真菌生长得更快。
综上,这部分在matlab里做初始化
m = 500;n = 500; % 元胞自动机的空间大小
% 用1, 2, 3 分别表示 S, E, I, R. 无养分区用 0 表示
% S = 未分解木质纤维 ; E = 弱势菌 ; R = 强势菌
[S, E, R] = deal(0,1,2); %deal就是匹配输出 相互对应出来的 使其一一对应
%可能这种代码意味着初始最多有两种状态,就是初始状态终止状态和啥也不是态
%rhoN = 0.00008;
rhoS = 0.9995; %初始未分解木质纤维密度
rhoE = 0.0004; % 初始弱势菌密度
rhoR = 0.0001;% 初始强势菌密度
% X 为每一个元胞的状态
X = zeros(m,n); % 先建立一个全零矩阵
%X(rand(m,n)<rhoN) = N;
X(rand(m,n)<rhoS) = S; % 如果随机的一个是小于0.96的,就是未分解木质纤维
X(rand(m,n)<rhoE) = E; %也是同上了 先定义上啊
X(rand(m,n)<rhoR) = R;
time = zeros(m,n); %计时: 用于计算潜伏时间和治疗时间 从 0 开始吗 ?
% 邻居方位
d = {[1,0], [0,1], [-1,0], [0,-1],[1,1], [-1,1], [-1,-1], [1,-1]};
%下面是一种状态转换为另一种状态的时间
T = 1; % S-E的时间,对应弱菌的实际生长率
D = 3; % S-R的时间,对应强菌的实际生长率
P1 = 0.6; % 弱菌孢子存活率
P2 = 0.5; % 强菌孢子存活率
P3 = 0.05; %强势菌吃掉弱势菌的概率
% 每一个元胞的潜伏期和治愈时间服从均值为 T 和 D 的正态分布
Tmn = normrnd(T,T/2,m,n); Dmn = normrnd(D,D/2,m,n); %正态分布的表示方法
状态转换如下图:

一开始系统中全部是未分解的木质纤维,随后大部分被弱势菌分解并替代,当大部分的地方都被强势菌和弱势菌占领后,开始两种菌之间的竞争作用,最后强势菌将完全覆盖掉弱势菌。

元胞数量变化是这样的。
ifS2R_S = rand(m,n)<(N2*P2);%S-R
ifS2E_S = rand(m,n)<(N1*P1);%S-E
ifS2R_E = rand(m,n)<(N2*P3);%E-R
ifS2E_or_R_S = rand(m,n)<(N1*P1)|rand(m,n)<(N2*P2); %A|B
ifS2E_and_R_S = rand(m,n)<(N1*P1)&rand(m,n)<(N2*P2); %A&B
Rule1 = S*(isS & ~(ifS2R_S|ifS2E_S|ifS2R_E)) ;
Rule2 = R*isR;
Rule3 = R*(isE & ifS2R_E)+R*(isS & ifS2R_S);
Rule4 = E*(isE & (ifS2R_S|ifS2E_S|ifS2R_E-ifS2R_S|ifS2E_S))+E*(isS & (ifS2E_S- ifS2R_S&ifS2E_S)) ;
状态转换规则如上,主要一个状态如果不变的情况也要考虑。
总结
因为已经过了一年了,只写了一些当时还记忆深刻的东西,这里有全篇论文和可以直接跑的代码以及当时比赛时的一些手稿,有写论文中表述不清的问题可以看看手稿,公式有很多都是手推的,但是论文只写了结果。由于论文中有篇幅限制,元胞自动机中的状态转换图放在手稿中了。整理不易,希望大家理解。