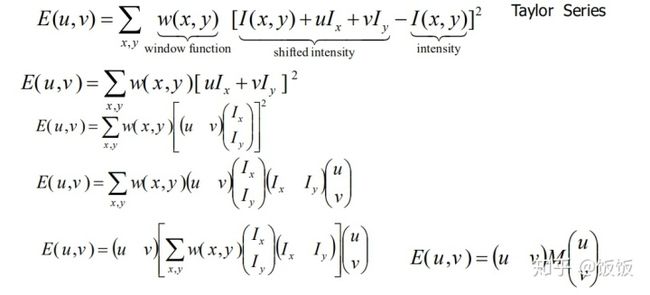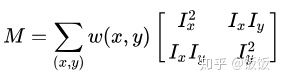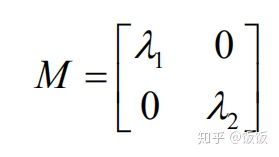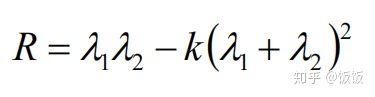harris角点检测_计算机视觉基础-图像处理: Harris特征点检测

1 简介

在图像处理领域中，特征点又被称为兴趣点或者角点，它通常具有旋转不变性和光照不变性和视角不变性等优点，是图像的重要特征之一，常被应用到目标匹配、目标跟踪、三维重建等应用中。点特征主要指图像中的明显点，如突出的角点、边缘端点、极值点等等，用于点特征提取的算子称为兴趣点提取（检测）算子，常用的有Harris角点检测、SIFT特征检测、FAST特征检测及SURF特征检测。

2 基础知识

2.1 角点基础知识

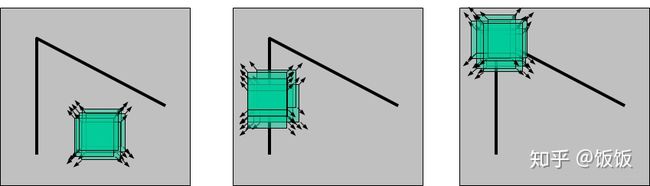
使用一个滑动窗口在下面三幅图中滑动，可以得出以下结论：

• 左图表示一个平坦区域，在各方向移动，窗口内像素值均没有太大变化；
• 中图表示一个边缘特征（Edges），如果沿着水平方向移动(梯度方向)，像素值会发生跳变；如果沿着边缘移动(平行于边缘) ，像素值不会发生变化；
• 右图表示一个角（Corners），不管你把它朝哪个方向移动，像素值都会发生很大变化。

除了上图最右边所示的角点，角点还有许多不同的类型。

2.2 图像梯度基础

“像素值发生很大变化”这一现象可以用图像梯度进行描述。在图像局部内，图像梯度越大表示该局部内像素值变化越大（灰度的变化率越大）。 而图像的梯度在数学上可用微分或者导数来表示。对于数字图像来说，相当于是二维离散函数求梯度，并使用差分来近似导数：Gx(x,y)=H(x+1,y)−H(x−1,y)Gy(x,y)=H(x,y+1)−H(x,y−1)在实际操作中，对图像求梯度通常是考虑图像的每个像素的某个邻域内的灰度变化，因此通常对原始图像中像素某个邻域设置梯度算子，然后采用小区域模板进行卷积来计算，常用的有Prewitt算子、Sobel算子、Robinson算子、Laplace算子等。

3 Harris角点检测算法原理

3.1 算法思想

算法的核心是利用局部窗口在图像上进行移动，判断灰度是否发生较大的变化。如果窗口内的灰度值（在梯度图上）都有较大的变化，那么这个窗口所在区域就存在角点。

这样就可以将 Harris 角点检测算法分为以下三步：

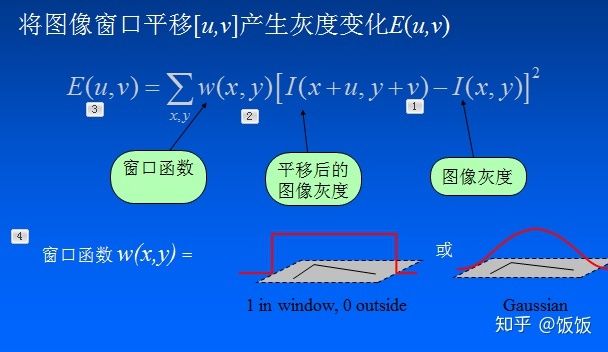
• 当窗口（局部区域）同时向 x （水平）和 y（垂直） 两个方向移动时，计算窗口内部的像素值变化量 E(x,y) ；
• 对于每个窗口，都计算其对应的一个角点响应函数 R；
• 然后对该函数进行阈值处理，如果 R>threshold，表示该窗口对应一个角点特征。

3.2 Harris角点数学模型

建立数学模型，确定哪些窗口会引起较大的灰度值变化。 让一个窗口的中心位于灰度图像的一个位置

，这个位置的像素灰度值为

，如果这个窗口分别向

和

方向移动一个小的位移

和

，到一个新的位置

，这个位置的像素灰度值就是

。

|就是窗口移动引起的灰度值的变化值。

设

为位置

处的窗口函数，表示窗口内各像素的权重，最简单的就是把窗口内所有像素的权重都设为1，即一个均值滤波核。

当然，也可以把

设定为以窗口中心为原点的高斯分布，即一个高斯核。如果窗口中心点像素是角点，那么窗口移动前后，中心点的灰度值变化非常强烈，所以该点权重系数应该设大一点，表示该点对灰度变化的贡献较大；而离窗口中心（角点）较远的点，这些点的灰度变化比较小，于是将权重系数设小一点，表示该点对灰度变化的贡献较小。

则窗口在各个方向上移动

所造成的像素灰度值的变化量公式如下：

若窗口内是一个角点，则E(u,v)的计算结果将会很大。

为了提高计算效率，对上述公式进行简化，利用泰勒级数展开来得到这个公式的近似形式：

其中对应的矩阵M为：

3.3 Harris角点求解

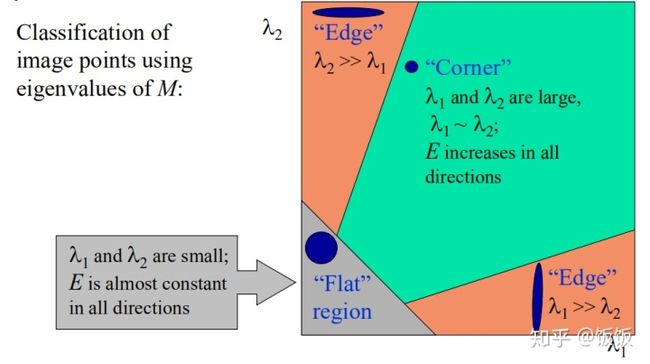
• 通过特征值

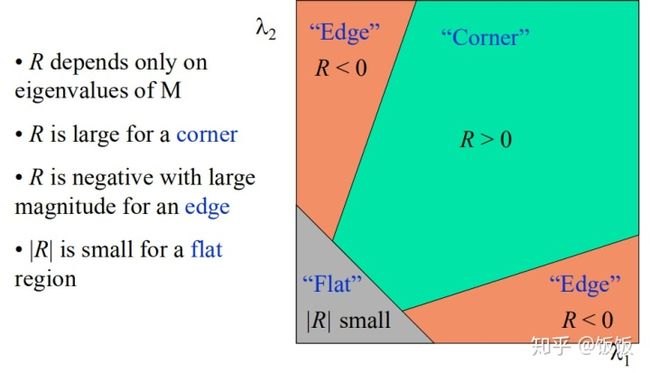
如果特征值在两个方向都比较大就是角点；如果特征值在一个方向比较大是边；如果特征值都很小就是平面。

可以把R看成旋转因子，其不影响两个正交方向的变化分量。经对角化处理后，将两个正交方向的变化分量提取出来，就是 λ1 和 λ2（特征值）。

• 通过R响应

因为特征值计算和判断起来比较麻烦，所以提出了和特征值对应的R相应进行简便的计算。

现在我们已经得到 E(u,v)的最终形式，别忘了我们的目的是要找到会引起较大的灰度值变化的那些窗口。

灰度值变化的大小则取决于矩阵M，M为梯度的协方差矩阵。在实际应用中为了能够应用更好的编程，所以定义了角点响应函数R，通过判定R大小来判断像素是否为角点。

计算每个窗口对应的得分（角点响应函数R定义）：

其中

是矩阵的行列式，

是矩阵的迹。

和

是矩阵

的特征值，

是一个经验常数，在范围 (0.04, 0.06) 之间。

R的值取决于M的特征值，对于角点

很大，平坦的区域

很小，边缘的

为负值。

因为特征值 λ1 和 λ2 决定了 R 的值，所以我们可以用特征值来决定一个窗口是平面、边缘还是角点：

• 平面:：该窗口在平坦区域上滑动，窗口内的灰度值基本不会发生变化，所以 |R| 值非常小，在水平和竖直方向的变化量均较小，即 Ix和 Iy都较小，那么 λ1 和 λ2 都较小；
• 边缘：|R|值为负数，仅在水平或竖直方向有较大的变化量，即 Ix和 Iy只有一个较大，也就是 λ1>>λ2 或 λ2>>λ1；
• 角点：[公式] 值很大，在水平、竖直两个方向上变化均较大的点，即 Ix和 Iy 都较大，也就是 λ1 和 λ2 都很大。

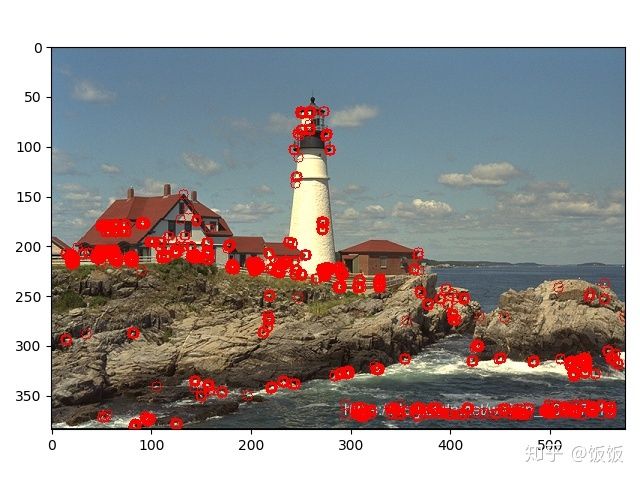
Harris 角点检测的结果是带有这些分数 R 的灰度图像，设定一个阈值，分数大于这个阈值的像素就对应角点。
如下图所示：

4 基于OpenCV的实现

4.1 参数介绍

在opencv中有提供实现 Harris 角点检测的函数 cv2.cornerHarris，我们直接调用的就可以，非常方便。

函数原型：cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])

对于每一个像素 (x,y)，在 (blockSize x blockSize) 邻域内，计算梯度图的协方差矩阵 M(x,y)，然后通过上面第二步中的角点响应函数得到结果图。图像中的角点可以为该结果图的局部最大值。

即可以得到输出图中的局部最大值，这些值就对应图像中的角点。

参数解释：

• src - 输入灰度图像，float32类型
• blockSize - 用于角点检测的邻域大小，就是上面提到的窗口的尺寸
• ksize - 用于计算梯度图的Sobel算子的尺寸
• k - 用于计算角点响应函数的参数k，取值范围常在0.04~0.06之间

4.2 代码示例

import cv2
from matplotlib import pyplot as plt
import numpy as np

# detector parameters
block_size = 3
sobel_size = 3
k = 0.06

image = cv2.imread('Figureharris_corner.png')

print(image.shape)
height = image.shape[0]
width = image.shape[1]
channels = image.shape[2]
print("width: %s  height: %s  channels: %s" % (width, height, channels))

gray_img = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# modify the data type setting to 32-bit floating point
gray_img = np.float32(gray_img)

# detect the corners with appropriate values as input parameters
corners_img = cv2.cornerHarris(gray_img, block_size, sobel_size, k)

# result is dilated for marking the corners, not necessary
# kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
# dst = cv2.dilate(corners_img, kernel)

dst = corners_img

# Threshold for an optimal value, marking the corners in Green
# image[corners_img>0.01*corners_img.max()] = [0,0,255]

for r in range(height):
    for c in range(width):
        pix = dst[r, c]
        if pix > 0.05 * dst.max():
            cv2.circle(image, (c, r), 5, (0, 0, 255), 0)

image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
plt.imshow(image)
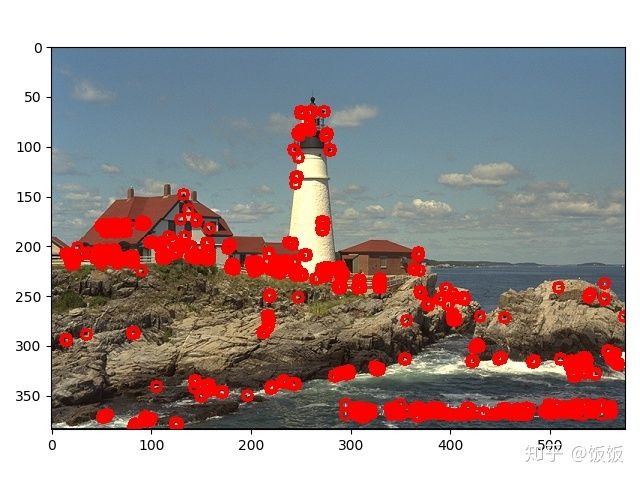
plt.show()

4.3 结果和分析

对Harris检测结果做 dilation 的结果如下 （感觉作用不大）

5 Harris 角点检测器特性

Harris角点检测的性质可总结如下：

• 阈值决定角点的数量
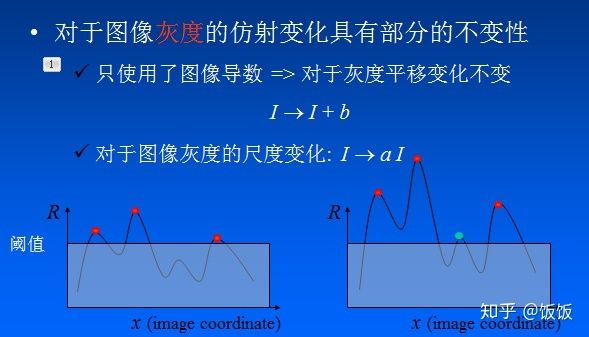
• 光照不变性：Harris角点检测算子对亮度和对比度的变化不敏感（光照不变性） 在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

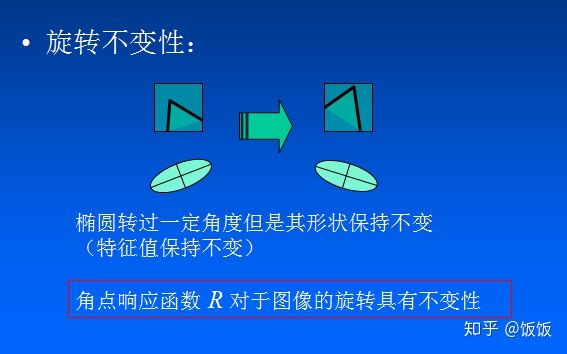
• 旋转不变性：Harris角点检测算子具有旋转不变性 Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

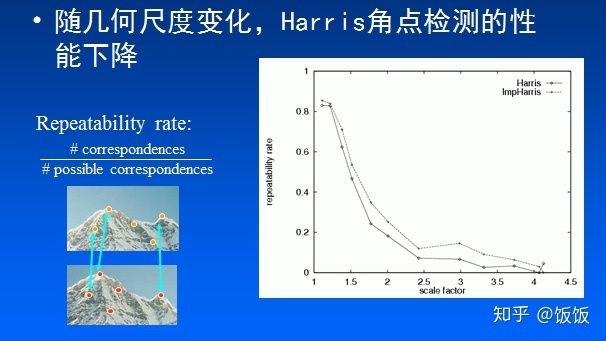
• 不具有尺度不变性：Harris角点检测算子不具有尺度不变性 尺度的变化会将角点变为边缘，或者边缘变为角点，Harris的理论基础并不具有尺度不变性。

参考

Datawhale 角点检测器

论文：《C.Harris, M.Stephens. “A Combined Corner and Edge Detector”. Proc. of 4th Alvey Vision Conference》

Harris角点算法

角点检测：Harris 与 Shi-Tomasi

https://www.cnblogs.com/ronny/p/4009425.html

https://blog.csdn.net/weixin_40647819