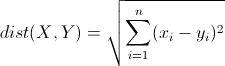K-Means算法及相关案例
K-Means算法及相关案例
大家好,我是W
K-Means作为机器学习的一个基础代码,显然稍微看过一点机器学习相关的内容的人都会听说过它。今天就来用实际代码讲K-Means算法的思想和原理。这篇文章的顺序是:1、K-Means算法原理 2、设计算法 3、案例1-普通K-Means算法代码实现。
1、K-Means算法原理
K-Means属于无监督学习算法,即在不知道数据集分类的情况下将相似的对象归到一个类(簇)中,是一种聚类。聚类和分类的差别在于是否知道训练集数据的分类,聚类是不知道的,而分类是知道的。
1.1 欧氏距离
K-Means算法的核心就是欧氏距离,通过欧氏距离可以在多维空间中计算出点的相近程度从而把最近的点归为一类。其具体公式为:
即X点和Y点的距离就是X、Y各维数据之差平方求和,最后取根号。
1.2 聚类步骤
K-Means算法存在一个质心的概念,就是该簇的中心点,而在算法开始的时候质心是随机生成的。下面通过流程图来解释算法:
可以看到流程图还是很简单的,这就是K-Means的最基本的思想:随机质心->更新样本类别->根据簇中样本更新质心->直到没有新的样本改变簇类别。
2、设计算法
在1.2中我们已经知道程序的流程图,但是还存在几个关键的步骤没有解决,在这里逐一列举出来:1、随机质心怎么做 2、样本到质心距离怎么计算 3、什么时候更新质心位置 4、如何判断样本归类有变化
2.1 如何随机质心
随机质心必须让质心保持在数据集的范围内,即每一维数据的最大最小值之内。同时根据分类数目(k)来构造质心数目。
def create_centers(data_matrix, k=4):
# 先把数计算出来降低时间复杂度
n, m = np.shape(data_matrix)
# 根据数据集创建随机质心 shape=[k,m] 保存质心的坐标
center_matrix = np.zeros(shape=(k, m))
for i in range(m):
min_val, max_val = min(data_matrix[:, i])[0, 0], max(data_matrix[:, i])[0, 0]
center_matrix[:, i] = np.array((min_val + (max_val - min_val) * np.random.rand(k, 1)))[:, 0]
center_matrix = np.mat(center_matrix)
return center_matrix
2.2 样本到质心距离计算
我们知道质心也是点,跟每一个样本是一样的,所以这个问题相对简单只需要按照欧氏距离的公式来计算即可。
def cal_distance(point_A, point_B):
point_A = point_A.A
point_B = point_B.A
distance = np.sqrt(np.sum(np.power((point_A - point_B), 2)))
return distance
2.3 数目时机更新质心位置
按照流程图的描述,更新质心位置需要在计算完每个样本到每个质心的距离之后,然后通过样本到其对应质心的距离的求和来更新质心位置。
2.4 如何判断样本归类发生变化
因为程序终止的条件是数据集中的样本的分类不再发生变化,反过来说就是只要数据集中存在一个样本的归类发生变化就需要重新计算。所以在死循环外需要建立一个flag来判断是否发生变化,然后在计算归类的时候需要有一个变量来记录该样本目前最优归类,需要一个变量来记录该样本上一次归类结果。
补充:所需要的数据结构
首先,对训练样本来说需要一个矩阵来存储。然后,因为需要记录每个样本的归类和该样本到其质心的距离,所以需要一个矩阵来存储归类和距离。最后,参与计算的还有质心矩阵,质心矩阵每一行代表一个质心,共k行。每一行结构根训练样本一样。
3、案例1-普通K-Means算法代码实现
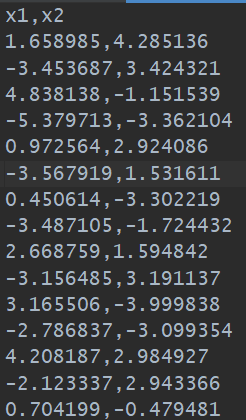
3.1 查看数据集
可以看到该数据集很简单,只有两列,存储格式是csv格式,整个数据集共有80个样本。肉眼观察就能知道没有缺失值。
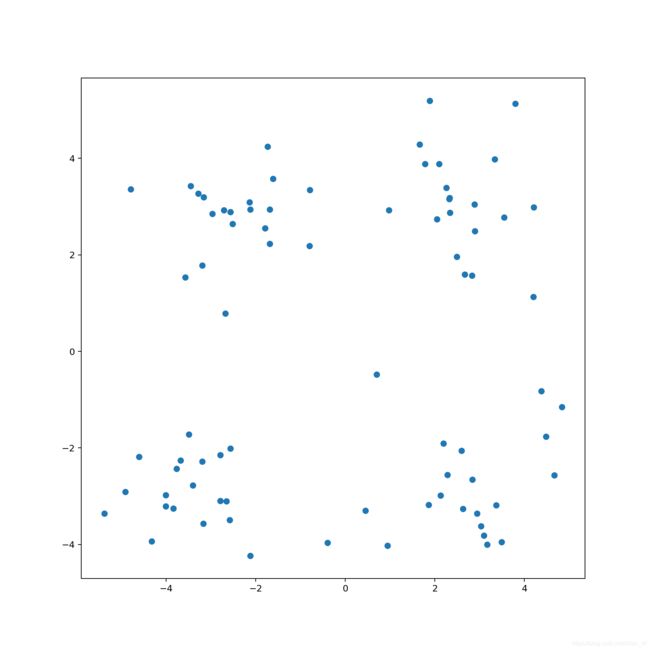
3.2 画图查看数据集
数据集很明显的分为4类,这也是观察容易看出来的,所以在后期分类的话就要分成4类。这是对于这个简单数据集来说的,若真实业务中可能会根据业务需求来分类。
3.3 程序整体流程
整个程序的流程是:加载数据->画出原始数据图->kmeans计算->画出kmeans聚类后的图
if __name__ == '__main__':
file_path = "./dataSet/data1.csv"
# 读数据
df = load_data(file_path)
# 画图
# my_paint(df)
# 转df为矩阵
data_matrix = np.mat(df)
# Kmeans算法分类
center_matrix = my_KMeans(data_matrix, 4)
# 画图2
my_paint_with_center(center_matrix, df)
3.4 读取数据
读取数据使用pandas的read_csv来读,很方便。因为要画图所以暂时用dataFrame格式。
def load_data(file_path):
df = pd.read_csv(file_path)
return df
3.5 KMeans算法
首先要生成分类矩阵
然后随机k个质心放入质心矩阵
用一个flag来标记循环
死循环判断是否有样本发生变化
两个循环对所有样本的所有质心计算记录
选择最优质心
判断样本质心变化,有则继续循环
更新质心坐标
def my_KMeans(data_matrix, k=4):
# 创建分类矩阵[n,2] n个样本 2列用于存质心index和到其对应质心的distance
cluster_matrix = np.zeros(shape=(len(data_matrix), 2))
# 创建随机质心矩阵
center_matrix = create_centers(data_matrix, k)
# 得到两个矩阵的shape
center_matrix_n, center_matrix_m = np.shape(center_matrix)
data_matrix_n, data_matrix_m = np.shape(data_matrix)
# 是否有变化flage
change_flag = True
# 直到没有变化为止结束
while change_flag:
change_flag = False
# 计算每一个点到每一个质心距离 取最小值归类
for i in range(data_matrix_n):
min_dist, min_index = math.inf, -1
for j in range(center_matrix_n):
# 计算距离
new_distance = cal_distance(data_matrix[i], center_matrix[j])
# 更新最近距离和质心index
if min_dist > new_distance:
min_dist = new_distance
min_index = j
# 若质心有变化 更新质心index
if min_index != cluster_matrix[i, 0]:
print("min_index != cluster_matrix[i, 0]", cluster_matrix[i, 0], min_index)
cluster_matrix[i, 0] = min_index
cluster_matrix[i, 1] = new_distance
change_flag = True
# 根据分类更新质心位置
for center in range(k):
# 从data_matrix中找到该类点 返回矩阵
# print(data_matrix[cluster_matrix[:, 0] == center])
# 对该矩阵求平均 axis表方向 0为列求平均 最后[1,m]
# print("avg:", np.average(data_matrix[cluster_matrix[:, 0] == center], axis=0))
center_matrix[center] = np.average(data_matrix[cluster_matrix[:, 0] == center], axis=0).A[0]
return center_matrix
最后的结果是这样的:
项目地址
点击进入github