MATLAB在聚类分析中的应用

（一）   引言：

“物以类聚，人以群分”，聚类分析作为一种重要的多元统计方法，广泛地应用于自然科学、社会科学、工农业生产的各个领域。本文仅以一个案例讲述在利用MATLAB软件实现聚类分析时所使用的函数以及聚类的方法和过程。

（二）案例重述：

我们对苏州所辖张家港市2003年七条河流中的主要污染因子（指标），即CODmn,BOD5,非离子氨，氨氮，挥发酚，石油类共6个变量（资料见下表，来源于张家港市2003年环境质量报告书），进行聚类分析。

 

河流	CODmn	BOD5	非离子氨	氨氮	挥发酚	石油类
张家港河	3.14	8.41	23.78	25.79	4.17	6.47
二干河	5.47	9.57	26.48	23.79	6.42	6.58
东横河	3.1	4．31	21.2	22.48	5.34	6.54
横套河	5.67	9.54	10.23	20.87	4.2	6.8
四干河	6.81	9.05	16.18	24.56	5.2	5.45
华妙河	6.21	7.08	21.05	31.56	6.15	8.21
盐铁塘	4.87	8.97	26.54	34.56	5.58	8.07

（三）函数解释:

1)  pdist函数

调用格式：Y=pdist(X,’metric’)

说明：用‘metric’指定的方法计算 X 数据矩阵中对象之间的距离。

metric’取值如下：

‘euclidean’：  欧氏距离（默认）；  ‘seuclidean’：标准化欧氏距离；

‘mahalanobis’：马氏距离；         ‘cityblock’：  洛克距离；

‘minkowski’： 明可夫斯基距离；

X是一个m×n的矩阵，Y是一个长为m(m–1)/2的行向量.

可以这样理解 Y的生成：首先生成一个 X 的距离方阵，由于该方阵是对称的，且对角线上的元素为0，所以取此方阵的下三角元素，按照Matlab中矩阵的按列存储原则，此下三角各元素的索引排列即为(2,1), (3,1),..., (m,1), (3,2), ..., (m,2), ..., (m,m–1).

2) squareform函数

调用格式：D=squareform(Y)
说明：  强制将距离矩阵从上三角形式转化为方阵形式，或从方阵形式转化为上三角形式。将pdist函数生成的行向量转化为方阵，其中 t(i,j)表示第 i个样本与第 j个样本之的距离，对角线均为 0.

3) linkage函数

调用格式：Z=linkage(Y,’method’)

说 明：用‘method’参数指定的算法计算系统聚类树。

method：可取值如下：

‘single’：最短距离法（默认）； ‘complete’：最长距离法；

‘average’：未加权平均距离法；‘weighted’： 加权平均法；

‘centroid’：质心距离法；     ‘median’：加权质心距离法；

‘ward’：内平方距离法（最小方差算法）

其中Y是pdist函数返回的距离向量；

返回：Z为一个包含聚类树信息的（m-1）×3的矩阵。其中前两列为索引标识，表示哪两个序号的样本可以聚为同一类，第三列为这两个样本之间的距离。另外，除了m个样本以外，对于每次新产生的类，依次用 m+1、 m+2、 …来标识。

4) dendrogram函数

调用格式：[H，T，…]=dendrogram(Z,p，…)

说明：生成只有顶部p个节点的冰柱图（谱系图）。

5) cluster函数

调用格式：T=cluster(Z,…)

说明：根据linkage函数的输出Z 创建分类。

（四）聚类方法及过程：

Ø Step1： 数据无量纲化

在多元统计分析中，各个指标由于计量单位和数量级不尽相同，从而使得各指标间不具有综合性，不能直接进行综合分析，这时就必须采用某种方法对各指标数值进行无量纲化处理，解决各指标数值不可综合性问题。消除量纲影响的方法有多种，在本案例的程序中采用的是标准差化方法，即每一变量值分别处以该变量的标准差，此外，还可以采用标准化方法（可以直接调用zscore函数）、均值化方法等。

ØStep2：寻找变量之间的相似性

利用pdist函数计算样本之间的距离，本案例中默认为欧氏距离，pdist生成一个 7*(7-1)/2个元素的行向量，分别表示 7个样本两两间的距离。   

D(2，1)=3.1688;

D(3，1)=2.6754;

D(4，1)=3.1361;

D(5，1)=3.2909;

D(6，1)=3.8705;

D(7，1)=3.1923;

D(3，2)=3.5882;

D(4，2)=3.8141;

D(5，2)=2.7127;

D(6，2)=2.8664;

D(7，2)=2.8693;

D(4，3)=4.0272;

D(5，3)=3.8880;

D(6，3)=3.7359;

D(7，3)=4.1058;

D(5，4)=2.3515;

D(6，4)=4.1167;

D(7，4)=4.4553;

D(6，5)=3.6402;

D(7，5)=4.0572;

D(7，6)=1.8834;

 

利用squareform函数，将上面的数据转化为方阵，同时，为了使对应关系更为直观，将方阵转化为下面的表格:

七条河流个体间欧氏距离的相似矩阵

案例	1：张家港河	2：二干河	3：东横河	4：横套河	5：四干河	6：华妙河	7：盐铁塘
1：张家港河	0	3.1688	2.6754	3.1361	3.2909	3.8705	3.1923
2：二干河	3.1688	0	3.5882	3.8141	2.7127	2.8664	2.8693
3：东横河	2.6754	3.5882	0	4.0272	3.8880	3.7359	4.1058
4：横套河	3.1361	3.8141	4.0272	0	2.3515	4.1167	4.4553
5：四干河	3.2909	2.7127	3.8880	2.3515	0	3.6402	4.0572
6：华妙河	3.8705	2.8664	3.7359	4.1167	3.6402	0	1.8834
7：盐铁塘	3.1923	2.8693	4.1058	4.4553	4.0572	1.8834	0

Ø Step3 ：定义变量之间的连接

样本6与样本7的距离最小（为1.8834），在层次聚类中将首先聚到一起形成一个新的小类记为第8类。接着，样本4与样本5聚到一起形成一个新的小类记为第9类。然后，样本1与样本3聚聚类顺序到一起形成一个新的小类记为第10类。样本2与第8，9，10类的最短欧氏距离依次为2.8664， 2.7127，3.1688，故接下来样本2会与第9类聚到一起形成一个新的小类记为第11类。样本6，7到样本1，2，3，4，5的最短距离是D(6，2)=2.8664，故样本2，4，5，6，7聚到一起，即第8类与第11类聚到一起成为第12类。样本1，3到样本2，4，5，6，7的最短距离是D(4，1)=3.1361，故1，2，3，4，5，6，7聚到一起，即第10类与第12类聚到一起。执行命令z=linkage(y)得到下面的结果：

z =

6.0000    7.0000    1.8834

4.0000    5.0000    2.3515

1.0000    3.0000    2.6754

2.0000    9.0000    2.7127

8.0000    11.0000    2.8664

10.0000   12.0000   3.1361

Ø Step4 创建聚类，并作出谱系图

聚类顺序

顺序	聚在一起的两类		最短距离
1	6	7	1.8834
2	4	5	2.3515
3	1	3	2.6754
4	2	9	2.7127
5	8	11	2.8664
6	10	12	3.1361

 

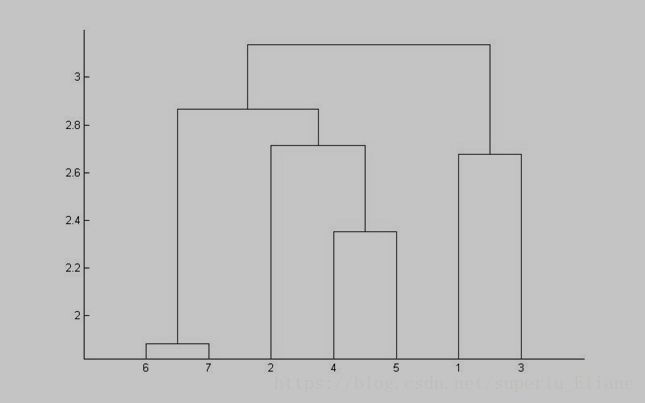
聚类谱系图

由该谱系图可以看出：

①       如果将样本分为4类，则样本1，3是一类，样本4，5是一类，样本6，7是一类，样本2单独一类

②       如果将样本分为3类，则样本1,3是一类，样本2,4,5是一类，样本6,7是一类

③       如果将样本分为2类，则样本1,3是一类，样本2,4,5,6,7是一类

④       最终所有的样本聚为一类。

（五）结论与评价：

从谱系图可以看出，七条河流中，二干河、横套河、四干河属于一类，污染较重，主要是CODmn、COD5超标多；花妙河、盐铁塘属于一类，污染一般，主要是氨氮、石油类超标；张家港河、东横河属于一类，污染较轻，总的来说，各河流都存在不同程度的污染，因此全市应对各河流严格监督管理，着力实施水污染防治工作，太湖流域水污染源应限期治理达标排放，巩固水污染防治工作成果，加大投入，新建或改、扩建废水治理工程，确保达标排放。

[参考资料]

[1].薛薇.统计分析与SPSS的应用.北京：中国人民大学出版社

[2]道客巴巴：http://www.doc88.com/p-17430638739.html

[3]道客巴巴：http://www.doc88.com/p-6905538103698.html

附录：MATLAB程序及运算结果

x =

    3.1400    8.4100  23.7800   25.7900    4.1700   6.4700

    5.4700    9.5700  26.4800   23.7900    6.4200   6.5800

    3.1000    4.3100  21.2000   22.4800    5.3400   6.5400

    5.6700    9.5400  10.2300   20.8700    4.2000   6.8000

    6.8100    9.0500  16.1800   24.5600    5.2000   5.4500

    6.2100    7.0800  21.0500   31.5600    6.1500   8.2100

    4.8700    8.9700  26.5400   34.5600    5.5800   8.0700

>> [m,n]=size(x)

m =7

n =6

>> stdr=std(x)

 stdr =1.4426    1.8880   5.8791    4.9921    0.8712   0.9669

 >> xx=x./stdr(ones(m,1),:)

 xx =

 

    2.1767    4.4545   4.0449    5.1662    4.7867   6.6913

    3.7918    5.0689   4.5041    4.7655    7.3694   6.8050

    2.1489    2.2829   3.6060    4.5031    6.1297   6.7636

    3.9305    5.0530   1.7401    4.1806    4.8211   7.0325

    4.7207    4.7935   2.7521    4.9198    5.9690   5.6364

    4.3048    3.7500   3.5805    6.3220    7.0595   8.4908

    3.3759    4.7511   4.5143    6.9229    6.4052   8.3460

 

>> y=pdist(xx)

y=

[3.1688,2.6754,3.1361,3.2909,3.8705,3.1923,3.5882,3.8141,2.7127,  2.8664,2.8693,4.0272,3.8880,3.7359,4.1058,2.3515,4.1167,4.4553    3.6402,4.0572,1.8834]

>> g=squareform(y)

g =

 

0         3.1688      2.6754      3.1361      3.2909     3.8705    3.1923

3.1688    0           3.5882      3.8141       2.7127    2.8664     2.8693

2.6754     3.5882      0          4.0272      3.8880     3.7359     4.1058

3.1361     3.8141      4.0272     0            2.3515      4.1167    4.4553

3.2909     2.7127      3.8880      2.3515      0          3.6402     4.0572

3.8705     2.8664      3.7359      4.1167      3.6402     0          1.8834

3.1923     2.8693      4.1058      4.4553      4.0572     1.8834    0

>> z=linkage(y)

z =

    6.0000    7.0000   1.8834

    4.0000    5.0000   2.3515

    1.0000    3.0000   2.6754

    2.0000    9.0000   2.7127

    8.0000   11.0000   2.8664

   10.0000   12.0000   3.1361

>> h= dendrogram(z)

h =

   173.0011

   175.0011

   176.0011

   177.0011

   178.0011

   179.0011

 

 

>>  t=cluster(z,4)

 

t =[4,1,4,2,2,3,3]’

 

>> t=cluster(z,3)

 

t =[3,2,3,2,2,1,1]’

 

>> t=cluster(z,2)

 

t =[1,2,1,2,2,2,2]’