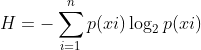机器学习决策树
基于《机器学习实战》理解并尝试决策树的实现。
目录
一、理解决策树
二、理解信息增益
三、构建决策树
四、图形化决策树
实验总结:
一、理解决策树
我们在日常生活中有时会遇到一些决策,做出不同的决策就应对着不同的结果。比如我们在回家时,是面临选择坐公交车,还是打车,做出选择时还需考虑自己的经济能力以及路途远近等因素。决策树就是在这样一种情形下诞生的。下面是决策树的一个模板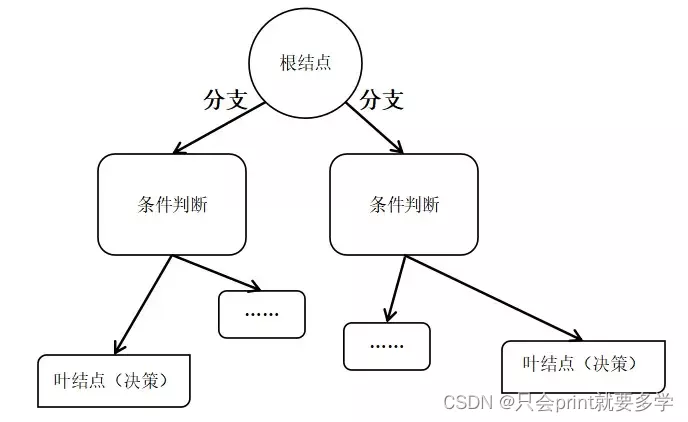
二、理解信息增益
上面提到,我们在回家要乘坐什么交通工具的时候,会依据自身经济能力以及路途远近等因素来考量,那么哪一个因素对于决策的影响更大,就需要应用信息增益来划分数据集。
划分数据集的大原则是:将无序数据变得更加有序,但是各种方法都有各自的优缺点。在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择,所以必须先学习如何计算信息增益,集合信息的度量方式称为香农熵,或者简称熵。
熵定义为信息的期望值,在明晰这个概念之前,我们必须知道信息的定义。如果待分类的事务可能划分在多个分类之中,则符号xi的定义为:
![]()
其中p(xi)是选择该分类的概率
为了计算熵,我们需要计算所有类别所有可能值包含的信息期望值,通过下面公式得到
书上还介绍另一种基尼不纯度,但是本次实验中不使用基尼不纯度方法,故不介绍
得到熵之后,我们就可以按照获取最大信息增益的方法划分数据集。
三、构建决策树
在了解了以最大信息增益的方式划分数据集后,我们就可以构建决策树了,构造流程如下:首先遍历整个数据集,计算每一个特征的香农熵,之后在按香农熵最大的划分数据集,之后得到若干个划分后的数据集,在对划分后的数据集计算香农熵,再按香农熵最大的划分数据集,以此类推,直到遍历完所有划分数据集的属性,或者每个分支下的所有实例都具有相同的分类,这样,程序便终止了。
但是世上万物都不可能是绝对的,数据集中的有些数据并不会完全符合预期,比如,你身上有足够的钱,并且回家的路途也很遥远,但是你也愿意骑共享单车回家,所以,在实际运用中,我们会多采用多数表决的方法决定叶子结点的分类
本次实验中,决策树是以字典集的方式呈现的,树的分支是以嵌套字典的形式展现。
每次下课,同学们的第一件事就是会问朋友们去哪吃,以此列出以下四个特征:
'外出意愿':0代表不想外出,1代表可以外出
'生活费是否充足 ':0代表生活费不充足,1代表生活费充足
' 饱腹程度':0代表饿,1代表不是很饿
'时间是否充足 ':0代表有时间,1代表没时间
| 外出意愿 | 生活费是否充足 | 饱腹程度 | 时间是否充足 | 结论 |
| 0 | 0 | 0 | 0 | 食堂 |
| 0 | 0 | 0 | 1 | 食堂 |
| 0 | 0 | 1 | 0 | 食堂 |
| 0 | 0 | 1 | 1 | 西餐厅 |
| 0 | 1 | 0 | 0 | 食堂 |
| 0 | 1 | 0 | 1 | 自助 |
| 0 | 1 | 1 | 0 | 食堂 |
| 0 | 1 | 1 | 1 | 西餐厅 |
| 1 | 0 | 0 | 0 | 食堂 |
| 1 | 0 | 0 | 1 | 食堂 |
| 1 | 0 | 1 | 0 | 食堂 |
| 1 | 0 | 1 | 1 | 西餐厅 |
| 1 | 1 | 0 | 0 | 西餐厅 |
| 1 | 1 | 0 | 1 | 自助 |
| 1 | 1 | 1 | 0 | 西餐厅 |
| 1 | 1 | 1 | 1 | 西餐厅 |
代码实现:
导入数据集:
def createDataSet():
dataSet = [[0, 0, 0, 0,'canteen'], #数据集
[0, 0, 0, 1,'canteen'],
[0, 0, 1, 0, 'canteen'],
[0, 0, 1, 1, 'restaurant'],
[0, 1, 0, 0,'canteen'],
[0, 1, 0, 1,'buffer'],
[0, 1, 1, 0,'canteen'],
[0, 1, 1, 1,'restaurant'],
[1, 0, 0, 0, 'canteen'],
[1, 0, 0, 1,'canteen'],
[1, 0, 1, 0, 'canteen'],
[1, 0, 1, 1,'restaurant'],
[1, 1, 0, 0, 'restaurant'],
[1, 1, 0, 1, 'buffer'],
[1, 1, 1, 0, 'restaurant'],
[1, 1, 1, 1, 'restaurant']]
labels = ['外出意愿', '生活费是否充足', '饱腹程度','时间是否充足'] #分类属性
return dataSet, labels
计算给定数据集的香农熵:
def calcShannonEnt(dataSet):
numEntires = len(dataSet)
labelCounts = {}
#对每一行取标签并计数标签的次数
for featVec in dataSet:
#取分类标签
currentLabel = featVec[-1]
#如果标签(Label)没有放入统计次数的字典,添加进去,有则加1
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
#计算香农熵
for key in labelCounts:
#计算概率然后依次取log2累加,套公式
prob = float(labelCounts[key]) / numEntires
shannonEnt -= prob * log(prob, 2)
return shannonEnt按照给定特征划分数据集:
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
#取与value特征相同的第axis项数据
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
#将去掉axis特征的数据加入retDataset中
retDataSet.append(reducedFeatVec)
return retDataSet例如,选择第0项为1的数据:
选择最好的数据集划分方式:
先计算数据集的原始熵值并保存,再对每一个属性值划分一次数据集,计算数据集的新熵值,并对所有唯一特征值求得的熵求和。最后比较所有特征中的信息增益,返回最好特征划分的索引。
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
#计算数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
#最优特征索引
bestFeature = -1
for i in range(numFeatures):
#获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
#subDataSet划分后的子集
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
#计算子集的熵
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
#取最大的信息增益
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
在一次筛选中,输出的值即为最大信息增益的特征,结果是2即表示以第2个特征划分是最好的,经过这一次筛选,labels中就不在有第2个特征了
创建决策树:
创建决策树的过程就是一个递归调用的过程,上文提到,递归结束的条件是程序遍历完所有的划分数据集的属性或者是剩下的分支的类别都相同,以这两个为递归结束出口编写代码
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet]
#如果类别完全相同则停止继续划分
if classList.count(classList[0]) == len(classList):
return classList[0]
#遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0]) == 1:
return majorityCnt(classList)
#选择最优特征
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
featLabels.append(bestFeatLabel)
#根据最优特征的标签生成树
myTree = {bestFeatLabel:{}}
#删除已经使用特征标签
del(labels[bestFeat])
#得到训练集中所有最优特征的属性值
featValues = [example[bestFeat] for example in dataSet]
#去掉重复的属性值
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels=labels[:]
#递归调用函数createTree(),遍历特征,创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree程序运行结果:
可以看到,该决策树是以饱腹程度为最大信息增益来分类的,为了让结果更直观,下面介绍用图形化展现决策树
四、图形化决策树
为了让结果更直观,我们将原先字典集形式的树在matplotlib上画出来
导包:
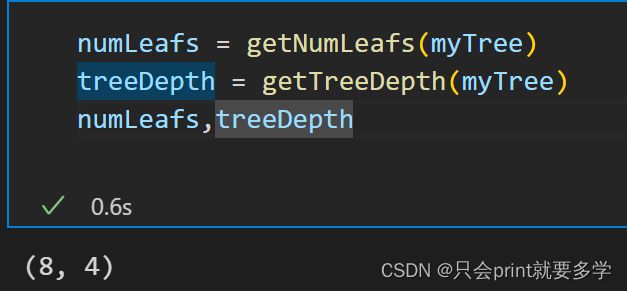
求出决策树的深度以及叶子节点个数:
为了让图像整体呈现居中的观感,我们需要提前获取决策树的叶子节点个数以及树的层数,这样我们在作画时就可以让根节点在画布正上方,然后根据层数以及叶子节点数让树的整体与画布相适应
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree)[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
#测试节点类型是否为字典,是则继续递归下去,不是则代表是叶子节点,计数+1
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs += 1
return numLeafsdef getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree)[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
#测试节点类型是否为字典
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
#比较深度
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth运行结果如下:8个叶子节点,4层深度
图形相关参数设置:
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
#箭头设置
arrow_args = dict(arrowstyle="<-")
#字体设置
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
#绘制结点
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args,fontproperties=font)
计算标注位置:
def plotMidText(cntrPt, parentPt, txtString):
#计算标注位置
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
绘制决策树:
绘制决策树的过程也是一个递归调用的过程。
def plotTree(myTree, parentPt, nodeTxt):
#设置结点格式
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
#设置叶结点格式
leafNode = dict(boxstyle="round4", fc="0.8")
#获取决策树叶结点数目以及树的层数
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstStr = next(iter(myTree))
#中心位置
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
#标注有向边属性值
plotMidText(cntrPt, parentPt, nodeTxt)
#绘制结点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
#继续绘制下一个节点
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
创建绘图面板:
def createPlot(inTree):
#创建fig
fig = plt.figure(1, facecolor='white')
#清空fig
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
#获取决策树叶结点数目以及树的层数
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
#绘制决策树
plotTree(inTree, (0.5,1.0), '')
plt.show()
最后根据数据集绘出的决策树图如下:
实验总结:
决策树的优点:
1.决策树易于理解,可以可视化分析,易提取规则
2.可以处理一些有确实属性的样本
3.测试数据集时运行速度快
决策树的缺点:
1.容易发生过拟合(课上提及随机森林可以大幅减少过拟合)
2.ID3算法计算信息增益时结果会偏向数值比较多的特征。