《视觉slam十四讲》学习笔记——ch7实践部分 比较opencv库下的ORB特征的提取和手写ORB的区别

    在学习了《视觉slam十四讲》第七章视觉里程计的相关知识后，运行了里面的基于opencv库函数的ORB特征点提取和匹配的代码。在使用代码自带的模板图片时，出来的效果很好，特征点匹配成功率很高，一方面原因是两张模板照片拍摄角度相差不大，于是我自己拍摄了两张照片，一张是正面照片，一张是侧面照片，再次使用该代码进行特征点匹配时发现误匹配的概率有点高，效果图如下：

1.两种方法的效果图

图1 基于opencv库函数的特征点匹配

     同时我在书上发现了手写的ORB特征点提取和匹配算法，这个算法是根据之前的ORB特征点原理而写的， 这里附上手写ORB的代码：

#include 
#include 
#include 
#include 

using namespace std;

// global variables
string first_file = "/home/rxz/桌面/3.jpeg";
string second_file = "/home/rxz/桌面/4.jpeg";

// 32 bit unsigned int, will have 8, 8x32=256
typedef vector DescType; // Descriptor type

/**
 * compute descriptor of orb keypoints
 * @param img input image
 * @param keypoints detected fast keypoints
 * @param descriptors descriptors
 *
 * NOTE: if a keypoint goes outside the image boundary (8 pixels), descriptors will not be computed and will be left as
 * empty
 */
void ComputeORB(const cv::Mat &img, vector &keypoints, vector &descriptors);

/**
 * brute-force match two sets of descriptors
 * @param desc1 the first descriptor
 * @param desc2 the second descriptor
 * @param matches matches of two images
 */
void BfMatch(const vector &desc1, const vector &desc2, vector &matches);

int main(int argc, char **argv) {

  // load image
  //加载图片
  cv::Mat first_image = cv::imread(first_file, 0);//0为灰度图
  cv::Mat second_image = cv::imread(second_file, 0);
  assert(first_image.data != nullptr && second_image.data != nullptr);

  // detect FAST keypoints1 using threshold=40
  //检测FAST关键点并构造描述函数
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  vector keypoints1;
  cv::FAST(first_image, keypoints1, 40);//ORB特征点的计算放在keypoints1容器中，利用FAST函数
  vector descriptor1;
  ComputeORB(first_image, keypoints1, descriptor1);//描述子的计算是自定义函数ComputeORB()

  // same for the second
  //同上
  vector keypoints2;
  vector descriptor2;
  cv::FAST(second_image, keypoints2, 40,true);//40是中心像素和围绕该像素的圆的像素之间的亮度差阈值
  ComputeORB(second_image, keypoints2, descriptor2);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration time_used = chrono::duration_cast>(t2 - t1);
  cout << "extract ORB cost = " << time_used.count() << " seconds. " << endl;

  // 暴力匹配法找匹配点
  vector matches;
  t1 = chrono::steady_clock::now();
  BfMatch(descriptor1, descriptor2, matches);//寻找相似特征点
  t2 = chrono::steady_clock::now();
  time_used = chrono::duration_cast>(t2 - t1);
  cout << "match ORB cost = " << time_used.count() << " seconds. " << endl;
  cout << "matches: " << matches.size() << endl;

  // plot the matches
  //连线匹配点，画图
  cv::Mat image_show;
  cv::drawMatches(first_image, keypoints1, second_image, keypoints2, matches, image_show);
  cv::imshow("matches", image_show);
  cv::imwrite("matches.png", image_show);
  cv::waitKey(0);

  cout << "done." << endl;
  return 0;
}

// -------------------------------------------------------------------------------------------------- //
// ORB pattern
//pragma region ORB_pattern[256 * 4]相当于在以关键点为中心[-13,12]的范围内,随机选点对p,q;进行关键点的向量构建
//这个变量里的数字，在ORBSLAM的代码中总共是256行，代表了256个点对儿，也就是每一个都代表了一对点的坐标，
//如第一行表示点q1(8,-3) 和点 q2(9,5), 接下来就是要对比这两个坐标对应的像素值的大小；
//为了保持踩点固定，工程上采用特殊设计的固定的pattern来做
int ORB_pattern[256 * 4] = {
  8, -3, 9, 5/*mean (0), correlation (0)*/,
  4, 2, 7, -12/*mean (1.12461e-05), correlation (0.0437584)*/,
  -11, 9, -8, 2/*mean (3.37382e-05), correlation (0.0617409)*/,
  7, -12, 12, -13/*mean (5.62303e-05), correlation (0.0636977)*/,
  2, -13, 2, 12/*mean (0.000134953), correlation (0.085099)*/,
  1, -7, 1, 6/*mean (0.000528565), correlation (0.0857175)*/,
  -2, -10, -2, -4/*mean (0.0188821), correlation (0.0985774)*/,
  -13, -13, -11, -8/*mean (0.0363135), correlation (0.0899616)*/,
  -13, -3, -12, -9/*mean (0.121806), correlation (0.099849)*/,
  10, 4, 11, 9/*mean (0.122065), correlation (0.093285)*/,
  -13, -8, -8, -9/*mean (0.162787), correlation (0.0942748)*/,
  -11, 7, -9, 12/*mean (0.21561), correlation (0.0974438)*/,
  7, 7, 12, 6/*mean (0.160583), correlation (0.130064)*/,
  -4, -5, -3, 0/*mean (0.228171), correlation (0.132998)*/,
  -13, 2, -12, -3/*mean (0.00997526), correlation (0.145926)*/,
  -9, 0, -7, 5/*mean (0.198234), correlation (0.143636)*/,
  12, -6, 12, -1/*mean (0.0676226), correlation (0.16689)*/,
  -3, 6, -2, 12/*mean (0.166847), correlation (0.171682)*/,
  -6, -13, -4, -8/*mean (0.101215), correlation (0.179716)*/,
  11, -13, 12, -8/*mean (0.200641), correlation (0.192279)*/,
  4, 7, 5, 1/*mean (0.205106), correlation (0.186848)*/,
  5, -3, 10, -3/*mean (0.234908), correlation (0.192319)*/,
  3, -7, 6, 12/*mean (0.0709964), correlation (0.210872)*/,
  -8, -7, -6, -2/*mean (0.0939834), correlation (0.212589)*/,
  -2, 11, -1, -10/*mean (0.127778), correlation (0.20866)*/,
  -13, 12, -8, 10/*mean (0.14783), correlation (0.206356)*/,
  -7, 3, -5, -3/*mean (0.182141), correlation (0.198942)*/,
  -4, 2, -3, 7/*mean (0.188237), correlation (0.21384)*/,
  -10, -12, -6, 11/*mean (0.14865), correlation (0.23571)*/,
  5, -12, 6, -7/*mean (0.222312), correlation (0.23324)*/,
  5, -6, 7, -1/*mean (0.229082), correlation (0.23389)*/,
  1, 0, 4, -5/*mean (0.241577), correlation (0.215286)*/,
  9, 11, 11, -13/*mean (0.00338507), correlation (0.251373)*/,
  4, 7, 4, 12/*mean (0.131005), correlation (0.257622)*/,
  2, -1, 4, 4/*mean (0.152755), correlation (0.255205)*/,
  -4, -12, -2, 7/*mean (0.182771), correlation (0.244867)*/,
  -8, -5, -7, -10/*mean (0.186898), correlation (0.23901)*/,
  4, 11, 9, 12/*mean (0.226226), correlation (0.258255)*/,
  0, -8, 1, -13/*mean (0.0897886), correlation (0.274827)*/,
  -13, -2, -8, 2/*mean (0.148774), correlation (0.28065)*/,
  -3, -2, -2, 3/*mean (0.153048), correlation (0.283063)*/,
  -6, 9, -4, -9/*mean (0.169523), correlation (0.278248)*/,
  8, 12, 10, 7/*mean (0.225337), correlation (0.282851)*/,
  0, 9, 1, 3/*mean (0.226687), correlation (0.278734)*/,
  7, -5, 11, -10/*mean (0.00693882), correlation (0.305161)*/,
  -13, -6, -11, 0/*mean (0.0227283), correlation (0.300181)*/,
  10, 7, 12, 1/*mean (0.125517), correlation (0.31089)*/,
  -6, -3, -6, 12/*mean (0.131748), correlation (0.312779)*/,
  10, -9, 12, -4/*mean (0.144827), correlation (0.292797)*/,
  -13, 8, -8, -12/*mean (0.149202), correlation (0.308918)*/,
  -13, 0, -8, -4/*mean (0.160909), correlation (0.310013)*/,
  3, 3, 7, 8/*mean (0.177755), correlation (0.309394)*/,
  5, 7, 10, -7/*mean (0.212337), correlation (0.310315)*/,
  -1, 7, 1, -12/*mean (0.214429), correlation (0.311933)*/,
  3, -10, 5, 6/*mean (0.235807), correlation (0.313104)*/,
  2, -4, 3, -10/*mean (0.00494827), correlation (0.344948)*/,
  -13, 0, -13, 5/*mean (0.0549145), correlation (0.344675)*/,
  -13, -7, -12, 12/*mean (0.103385), correlation (0.342715)*/,
  -13, 3, -11, 8/*mean (0.134222), correlation (0.322922)*/,
  -7, 12, -4, 7/*mean (0.153284), correlation (0.337061)*/,
  6, -10, 12, 8/*mean (0.154881), correlation (0.329257)*/,
  -9, -1, -7, -6/*mean (0.200967), correlation (0.33312)*/,
  -2, -5, 0, 12/*mean (0.201518), correlation (0.340635)*/,
  -12, 5, -7, 5/*mean (0.207805), correlation (0.335631)*/,
  3, -10, 8, -13/*mean (0.224438), correlation (0.34504)*/,
  -7, -7, -4, 5/*mean (0.239361), correlation (0.338053)*/,
  -3, -2, -1, -7/*mean (0.240744), correlation (0.344322)*/,
  2, 9, 5, -11/*mean (0.242949), correlation (0.34145)*/,
  -11, -13, -5, -13/*mean (0.244028), correlation (0.336861)*/,
  -1, 6, 0, -1/*mean (0.247571), correlation (0.343684)*/,
  5, -3, 5, 2/*mean (0.000697256), correlation (0.357265)*/,
  -4, -13, -4, 12/*mean (0.00213675), correlation (0.373827)*/,
  -9, -6, -9, 6/*mean (0.0126856), correlation (0.373938)*/,
  -12, -10, -8, -4/*mean (0.0152497), correlation (0.364237)*/,
  10, 2, 12, -3/*mean (0.0299933), correlation (0.345292)*/,
  7, 12, 12, 12/*mean (0.0307242), correlation (0.366299)*/,
  -7, -13, -6, 5/*mean (0.0534975), correlation (0.368357)*/,
  -4, 9, -3, 4/*mean (0.099865), correlation (0.372276)*/,
  7, -1, 12, 2/*mean (0.117083), correlation (0.364529)*/,
  -7, 6, -5, 1/*mean (0.126125), correlation (0.369606)*/,
  -13, 11, -12, 5/*mean (0.130364), correlation (0.358502)*/,
  -3, 7, -2, -6/*mean (0.131691), correlation (0.375531)*/,
  7, -8, 12, -7/*mean (0.160166), correlation (0.379508)*/,
  -13, -7, -11, -12/*mean (0.167848), correlation (0.353343)*/,
  1, -3, 12, 12/*mean (0.183378), correlation (0.371916)*/,
  2, -6, 3, 0/*mean (0.228711), correlation (0.371761)*/,
  -4, 3, -2, -13/*mean (0.247211), correlation (0.364063)*/,
  -1, -13, 1, 9/*mean (0.249325), correlation (0.378139)*/,
  7, 1, 8, -6/*mean (0.000652272), correlation (0.411682)*/,
  1, -1, 3, 12/*mean (0.00248538), correlation (0.392988)*/,
  9, 1, 12, 6/*mean (0.0206815), correlation (0.386106)*/,
  -1, -9, -1, 3/*mean (0.0364485), correlation (0.410752)*/,
  -13, -13, -10, 5/*mean (0.0376068), correlation (0.398374)*/,
  7, 7, 10, 12/*mean (0.0424202), correlation (0.405663)*/,
  12, -5, 12, 9/*mean (0.0942645), correlation (0.410422)*/,
  6, 3, 7, 11/*mean (0.1074), correlation (0.413224)*/,
  5, -13, 6, 10/*mean (0.109256), correlation (0.408646)*/,
  2, -12, 2, 3/*mean (0.131691), correlation (0.416076)*/,
  3, 8, 4, -6/*mean (0.165081), correlation (0.417569)*/,
  2, 6, 12, -13/*mean (0.171874), correlation (0.408471)*/,
  9, -12, 10, 3/*mean (0.175146), correlation (0.41296)*/,
  -8, 4, -7, 9/*mean (0.183682), correlation (0.402956)*/,
  -11, 12, -4, -6/*mean (0.184672), correlation (0.416125)*/,
  1, 12, 2, -8/*mean (0.191487), correlation (0.386696)*/,
  6, -9, 7, -4/*mean (0.192668), correlation (0.394771)*/,
  2, 3, 3, -2/*mean (0.200157), correlation (0.408303)*/,
  6, 3, 11, 0/*mean (0.204588), correlation (0.411762)*/,
  3, -3, 8, -8/*mean (0.205904), correlation (0.416294)*/,
  7, 8, 9, 3/*mean (0.213237), correlation (0.409306)*/,
  -11, -5, -6, -4/*mean (0.243444), correlation (0.395069)*/,
  -10, 11, -5, 10/*mean (0.247672), correlation (0.413392)*/,
  -5, -8, -3, 12/*mean (0.24774), correlation (0.411416)*/,
  -10, 5, -9, 0/*mean (0.00213675), correlation (0.454003)*/,
  8, -1, 12, -6/*mean (0.0293635), correlation (0.455368)*/,
  4, -6, 6, -11/*mean (0.0404971), correlation (0.457393)*/,
  -10, 12, -8, 7/*mean (0.0481107), correlation (0.448364)*/,
  4, -2, 6, 7/*mean (0.050641), correlation (0.455019)*/,
  -2, 0, -2, 12/*mean (0.0525978), correlation (0.44338)*/,
  -5, -8, -5, 2/*mean (0.0629667), correlation (0.457096)*/,
  7, -6, 10, 12/*mean (0.0653846), correlation (0.445623)*/,
  -9, -13, -8, -8/*mean (0.0858749), correlation (0.449789)*/,
  -5, -13, -5, -2/*mean (0.122402), correlation (0.450201)*/,
  8, -8, 9, -13/*mean (0.125416), correlation (0.453224)*/,
  -9, -11, -9, 0/*mean (0.130128), correlation (0.458724)*/,
  1, -8, 1, -2/*mean (0.132467), correlation (0.440133)*/,
  7, -4, 9, 1/*mean (0.132692), correlation (0.454)*/,
  -2, 1, -1, -4/*mean (0.135695), correlation (0.455739)*/,
  11, -6, 12, -11/*mean (0.142904), correlation (0.446114)*/,
  -12, -9, -6, 4/*mean (0.146165), correlation (0.451473)*/,
  3, 7, 7, 12/*mean (0.147627), correlation (0.456643)*/,
  5, 5, 10, 8/*mean (0.152901), correlation (0.455036)*/,
  0, -4, 2, 8/*mean (0.167083), correlation (0.459315)*/,
  -9, 12, -5, -13/*mean (0.173234), correlation (0.454706)*/,
  0, 7, 2, 12/*mean (0.18312), correlation (0.433855)*/,
  -1, 2, 1, 7/*mean (0.185504), correlation (0.443838)*/,
  5, 11, 7, -9/*mean (0.185706), correlation (0.451123)*/,
  3, 5, 6, -8/*mean (0.188968), correlation (0.455808)*/,
  -13, -4, -8, 9/*mean (0.191667), correlation (0.459128)*/,
  -5, 9, -3, -3/*mean (0.193196), correlation (0.458364)*/,
  -4, -7, -3, -12/*mean (0.196536), correlation (0.455782)*/,
  6, 5, 8, 0/*mean (0.1972), correlation (0.450481)*/,
  -7, 6, -6, 12/*mean (0.199438), correlation (0.458156)*/,
  -13, 6, -5, -2/*mean (0.211224), correlation (0.449548)*/,
  1, -10, 3, 10/*mean (0.211718), correlation (0.440606)*/,
  4, 1, 8, -4/*mean (0.213034), correlation (0.443177)*/,
  -2, -2, 2, -13/*mean (0.234334), correlation (0.455304)*/,
  2, -12, 12, 12/*mean (0.235684), correlation (0.443436)*/,
  -2, -13, 0, -6/*mean (0.237674), correlation (0.452525)*/,
  4, 1, 9, 3/*mean (0.23962), correlation (0.444824)*/,
  -6, -10, -3, -5/*mean (0.248459), correlation (0.439621)*/,
  -3, -13, -1, 1/*mean (0.249505), correlation (0.456666)*/,
  7, 5, 12, -11/*mean (0.00119208), correlation (0.495466)*/,
  4, -2, 5, -7/*mean (0.00372245), correlation (0.484214)*/,
  -13, 9, -9, -5/*mean (0.00741116), correlation (0.499854)*/,
  7, 1, 8, 6/*mean (0.0208952), correlation (0.499773)*/,
  7, -8, 7, 6/*mean (0.0220085), correlation (0.501609)*/,
  -7, -4, -7, 1/*mean (0.0233806), correlation (0.496568)*/,
  -8, 11, -7, -8/*mean (0.0236505), correlation (0.489719)*/,
  -13, 6, -12, -8/*mean (0.0268781), correlation (0.503487)*/,
  2, 4, 3, 9/*mean (0.0323324), correlation (0.501938)*/,
  10, -5, 12, 3/*mean (0.0399235), correlation (0.494029)*/,
  -6, -5, -6, 7/*mean (0.0420153), correlation (0.486579)*/,
  8, -3, 9, -8/*mean (0.0548021), correlation (0.484237)*/,
  2, -12, 2, 8/*mean (0.0616622), correlation (0.496642)*/,
  -11, -2, -10, 3/*mean (0.0627755), correlation (0.498563)*/,
  -12, -13, -7, -9/*mean (0.0829622), correlation (0.495491)*/,
  -11, 0, -10, -5/*mean (0.0843342), correlation (0.487146)*/,
  5, -3, 11, 8/*mean (0.0929937), correlation (0.502315)*/,
  -2, -13, -1, 12/*mean (0.113327), correlation (0.48941)*/,
  -1, -8, 0, 9/*mean (0.132119), correlation (0.467268)*/,
  -13, -11, -12, -5/*mean (0.136269), correlation (0.498771)*/,
  -10, -2, -10, 11/*mean (0.142173), correlation (0.498714)*/,
  -3, 9, -2, -13/*mean (0.144141), correlation (0.491973)*/,
  2, -3, 3, 2/*mean (0.14892), correlation (0.500782)*/,
  -9, -13, -4, 0/*mean (0.150371), correlation (0.498211)*/,
  -4, 6, -3, -10/*mean (0.152159), correlation (0.495547)*/,
  -4, 12, -2, -7/*mean (0.156152), correlation (0.496925)*/,
  -6, -11, -4, 9/*mean (0.15749), correlation (0.499222)*/,
  6, -3, 6, 11/*mean (0.159211), correlation (0.503821)*/,
  -13, 11, -5, 5/*mean (0.162427), correlation (0.501907)*/,
  11, 11, 12, 6/*mean (0.16652), correlation (0.497632)*/,
  7, -5, 12, -2/*mean (0.169141), correlation (0.484474)*/,
  -1, 12, 0, 7/*mean (0.169456), correlation (0.495339)*/,
  -4, -8, -3, -2/*mean (0.171457), correlation (0.487251)*/,
  -7, 1, -6, 7/*mean (0.175), correlation (0.500024)*/,
  -13, -12, -8, -13/*mean (0.175866), correlation (0.497523)*/,
  -7, -2, -6, -8/*mean (0.178273), correlation (0.501854)*/,
  -8, 5, -6, -9/*mean (0.181107), correlation (0.494888)*/,
  -5, -1, -4, 5/*mean (0.190227), correlation (0.482557)*/,
  -13, 7, -8, 10/*mean (0.196739), correlation (0.496503)*/,
  1, 5, 5, -13/*mean (0.19973), correlation (0.499759)*/,
  1, 0, 10, -13/*mean (0.204465), correlation (0.49873)*/,
  9, 12, 10, -1/*mean (0.209334), correlation (0.49063)*/,
  5, -8, 10, -9/*mean (0.211134), correlation (0.503011)*/,
  -1, 11, 1, -13/*mean (0.212), correlation (0.499414)*/,
  -9, -3, -6, 2/*mean (0.212168), correlation (0.480739)*/,
  -1, -10, 1, 12/*mean (0.212731), correlation (0.502523)*/,
  -13, 1, -8, -10/*mean (0.21327), correlation (0.489786)*/,
  8, -11, 10, -6/*mean (0.214159), correlation (0.488246)*/,
  2, -13, 3, -6/*mean (0.216993), correlation (0.50287)*/,
  7, -13, 12, -9/*mean (0.223639), correlation (0.470502)*/,
  -10, -10, -5, -7/*mean (0.224089), correlation (0.500852)*/,
  -10, -8, -8, -13/*mean (0.228666), correlation (0.502629)*/,
  4, -6, 8, 5/*mean (0.22906), correlation (0.498305)*/,
  3, 12, 8, -13/*mean (0.233378), correlation (0.503825)*/,
  -4, 2, -3, -3/*mean (0.234323), correlation (0.476692)*/,
  5, -13, 10, -12/*mean (0.236392), correlation (0.475462)*/,
  4, -13, 5, -1/*mean (0.236842), correlation (0.504132)*/,
  -9, 9, -4, 3/*mean (0.236977), correlation (0.497739)*/,
  0, 3, 3, -9/*mean (0.24314), correlation (0.499398)*/,
  -12, 1, -6, 1/*mean (0.243297), correlation (0.489447)*/,
  3, 2, 4, -8/*mean (0.00155196), correlation (0.553496)*/,
  -10, -10, -10, 9/*mean (0.00239541), correlation (0.54297)*/,
  8, -13, 12, 12/*mean (0.0034413), correlation (0.544361)*/,
  -8, -12, -6, -5/*mean (0.003565), correlation (0.551225)*/,
  2, 2, 3, 7/*mean (0.00835583), correlation (0.55285)*/,
  10, 6, 11, -8/*mean (0.00885065), correlation (0.540913)*/,
  6, 8, 8, -12/*mean (0.0101552), correlation (0.551085)*/,
  -7, 10, -6, 5/*mean (0.0102227), correlation (0.533635)*/,
  -3, -9, -3, 9/*mean (0.0110211), correlation (0.543121)*/,
  -1, -13, -1, 5/*mean (0.0113473), correlation (0.550173)*/,
  -3, -7, -3, 4/*mean (0.0140913), correlation (0.554774)*/,
  -8, -2, -8, 3/*mean (0.017049), correlation (0.55461)*/,
  4, 2, 12, 12/*mean (0.01778), correlation (0.546921)*/,
  2, -5, 3, 11/*mean (0.0224022), correlation (0.549667)*/,
  6, -9, 11, -13/*mean (0.029161), correlation (0.546295)*/,
  3, -1, 7, 12/*mean (0.0303081), correlation (0.548599)*/,
  11, -1, 12, 4/*mean (0.0355151), correlation (0.523943)*/,
  -3, 0, -3, 6/*mean (0.0417904), correlation (0.543395)*/,
  4, -11, 4, 12/*mean (0.0487292), correlation (0.542818)*/,
  2, -4, 2, 1/*mean (0.0575124), correlation (0.554888)*/,
  -10, -6, -8, 1/*mean (0.0594242), correlation (0.544026)*/,
  -13, 7, -11, 1/*mean (0.0597391), correlation (0.550524)*/,
  -13, 12, -11, -13/*mean (0.0608974), correlation (0.55383)*/,
  6, 0, 11, -13/*mean (0.065126), correlation (0.552006)*/,
  0, -1, 1, 4/*mean (0.074224), correlation (0.546372)*/,
  -13, 3, -9, -2/*mean (0.0808592), correlation (0.554875)*/,
  -9, 8, -6, -3/*mean (0.0883378), correlation (0.551178)*/,
  -13, -6, -8, -2/*mean (0.0901035), correlation (0.548446)*/,
  5, -9, 8, 10/*mean (0.0949843), correlation (0.554694)*/,
  2, 7, 3, -9/*mean (0.0994152), correlation (0.550979)*/,
  -1, -6, -1, -1/*mean (0.10045), correlation (0.552714)*/,
  9, 5, 11, -2/*mean (0.100686), correlation (0.552594)*/,
  11, -3, 12, -8/*mean (0.101091), correlation (0.532394)*/,
  3, 0, 3, 5/*mean (0.101147), correlation (0.525576)*/,
  -1, 4, 0, 10/*mean (0.105263), correlation (0.531498)*/,
  3, -6, 4, 5/*mean (0.110785), correlation (0.540491)*/,
  -13, 0, -10, 5/*mean (0.112798), correlation (0.536582)*/,
  5, 8, 12, 11/*mean (0.114181), correlation (0.555793)*/,
  8, 9, 9, -6/*mean (0.117431), correlation (0.553763)*/,
  7, -4, 8, -12/*mean (0.118522), correlation (0.553452)*/,
  -10, 4, -10, 9/*mean (0.12094), correlation (0.554785)*/,
  7, 3, 12, 4/*mean (0.122582), correlation (0.555825)*/,
  9, -7, 10, -2/*mean (0.124978), correlation (0.549846)*/,
  7, 0, 12, -2/*mean (0.127002), correlation (0.537452)*/,
  -1, -6, 0, -11/*mean (0.127148), correlation (0.547401)*/
};

// compute the descriptor
void ComputeORB(const cv::Mat &img, vector &keypoints, vector &descriptors) 
{
  const int half_patch_size = 8;
  const int half_boundary = 16;
  int bad_points = 0;
  for (auto &kp: keypoints) 
  {//在计算BRIEF描述子时，如果以该keypoints为中心的图像块，超出了图像范围则为坏点
    if (kp.pt.x < half_boundary || kp.pt.y < half_boundary ||
        kp.pt.x >= img.cols - half_boundary || kp.pt.y >= img.rows - half_boundary) 
        {
      // outside
      bad_points++;
      descriptors.push_back({});
      continue;
        }

    float m01 = 0, m10 = 0;
    for (int dx = -half_patch_size; dx < half_patch_size; ++dx) {
      for (int dy = -half_patch_size; dy < half_patch_size; ++dy) {
        uchar pixel = img.at(kp.pt.y + dy, kp.pt.x + dx);
        m10 += dx * pixel;
        m01 += dy * pixel;
      }
    }

    // 计算几何中心和质心的角度angle should be arc tan(m01/m10);
    float m_sqrt = sqrt(m01 * m01 + m10 * m10) + 1e-18; // avoid divide by zero
    float sin_theta = m01 / m_sqrt;
    float cos_theta = m10 / m_sqrt;

    // compute the angle of this point
    DescType desc(8, 0);
    for (int i = 0; i < 8; i++) {
      uint32_t d = 0;
      for (int k = 0; k < 32; k++) {
        int idx_pq = i * 32 + k;
        cv::Point2f p(ORB_pattern[idx_pq * 4], ORB_pattern[idx_pq * 4 + 1]);
        cv::Point2f q(ORB_pattern[idx_pq * 4 + 2], ORB_pattern[idx_pq * 4 + 3]);

        // rotate with theta
        cv::Point2f pp = cv::Point2f(cos_theta * p.x - sin_theta * p.y, sin_theta * p.x + cos_theta * p.y)
                         + kp.pt;
        cv::Point2f qq = cv::Point2f(cos_theta * q.x - sin_theta * q.y, sin_theta * q.x + cos_theta * q.y)
                         + kp.pt;
        if (img.at(pp.y, pp.x) < img.at(qq.y, qq.x)) {
          d |= 1 << k;
        }
      }
      desc[i] = d;
    }
    descriptors.push_back(desc);
  }

  cout << "bad/total: " << bad_points << "/" << keypoints.size() << endl;
}

// brute-force matching暴力匹配
void BfMatch(const vector &desc1, const vector &desc2, vector &matches) {
  const int d_max = 40;

  for (size_t i1 = 0; i1 < desc1.size(); ++i1) 
  {
    if (desc1[i1].empty()) continue;//如果第i1个描述子为空，则跳出此次循环
    cv::DMatch m{i1, 0, 256};//创建DMatch类的变量m，其中前两个分别是第一张图片的索引，queryIdx : 查询点的索引（当前要寻找匹配结果的点在它所在图片上的索引）。trainIdx : 被查询到的点的索引（存储库中的点的在存储库上的索引）。
                             //第三个参数是设定的汉明距离
    for (size_t i2 = 0; i2 < desc2.size(); ++i2)
     {
      if (desc2[i2].empty()) continue;
      int distance = 0;
      for (int k = 0; k < 8; k++) 
      {
        //这里的描述子是256位的，对应为8个32位的unsigned int数据，而这里的k表示第几个unsigned int数据
        distance += _mm_popcnt_u32(desc1[i1][k] ^ desc2[i2][k]);//利用sse指令集计算unsigned int变量中1的个数，从而计算汉明距离。a^b表示a与b按位异或；
      }
      if (distance < d_max && distance < m.distance) //在图像1中取一个描述子，然后计算与图像2中的所有描述子的汉明距离，把最近的那个距离找出来
      {
        m.distance = distance;
        m.trainIdx = i2;
      }
    }
    if (m.distance < d_max) 
    {
      matches.push_back(m);
    }
  }
}

手写ORB代码的效果图如下：

图2 手写ORB特征点提取和匹配算法效果图

 同时附上两种方法的运行时间：

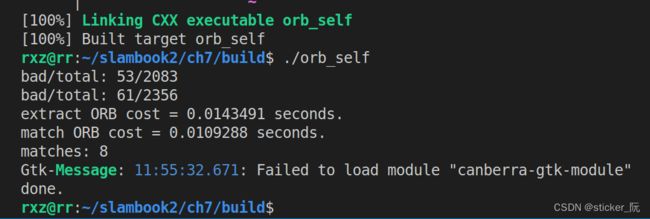
               图3 手写ORB特征点提取和匹配算法运行的时间

     图4 opencv特征点提取和匹配算法运行的时间

可以发现手写ORB特征点提取和匹配算法的特征点匹配成功率较高，匹配对较少，在上附图中只有8对匹配对。接下来分析比较两种代码的差别：

2.两种方法的差别

(1)FAST角点检测

opencv库函数：利用ORB特征检测器detector里的detect函数。

手写：利用改进的FAST算法，增加了中心像素和围绕该像素的圆的像素之间的强度差阈值以及非最大值抑制。
其中的FAST（）函数结构如下：

1.检测FAST关键点使用 cv::FAST()函数   

 CV_EXPORTS void FAST( InputArray image, CV_OUT std::vector& keypoints,
                      int threshold, bool nonmaxSuppression=true );

image： 检测的灰度图像

keypoints: 在图像上检测到的关键点

threshold: 中心像素和围绕该像素的圆的像素之间的强度差阈值

nonmaxSuppression: 参数非最大值抑制,默认为真，对检测到的角点应用非最大值抑制。

（2）描述子计算

opencv库函数：构建ORB特征描述器descriptor里的compute函数

手写：自定义函数ComputeORB()来计算描述子，在这个函数里面首先会排除一些靠近边缘的特征点。排除的坏点的判断方式如下：

1、当kp.pt.x < half_boundary时，边长为boundary的图像块将在-x轴上超出图像。
2、当kp.pt.y < half_boundary时，边长为boundary的图像块将在-y轴上超出图像。
3、当kp.pt.x >= img.cols - half_boundary（kp.pt.x>= 640-16）时，边长为boundary(32)的图像块将在+x轴上超出图像。
4、当kp.pt.y >= img.rows - half_boundary（kp.pt.y>= 480-16）时，边长为boundary(32)的图像块将在+y轴上超出图像。
同时，在手写代码中，按照灰度质心法定义了图像块的矩和质心，最后求出了特征点的角度。

在求描述子时，事先准备了256*4个数据集，这些数据集表示以关键点为中心，[-13,12]的范围内,随机选点对p,q。选取两个点p,q，这两个点的坐标从数据集选取，然后乘上之前求的角度再加上关键点，以此找到关键点附近的两个随机像素，然后比较像素值。最终形成描述子。

（3）BRIEF描述子匹配函数

opencv下：利用自带的match函数，比较两副图像的描述子的汉明距离，并从小到大排序在matches容器中，然后在容器中挑选好的描述子，这些描述子满足描述子之间的距离小于两倍的最小距离和经验阈值的最小值，因为最小距离可能是0；

手写代码中：描述子是采用256位二进制描述，对应到8个32位的unsigned int 数据，并利用SSE指令集计算每个unsigned int变量中1的个数，从而计算汉明距离。手写的暴力匹配代码中输入三个参数，分别是第一副和第二副图像的描述子，和存放输出匹配对的容器；这里的暴力匹配的思路为：取第一副图片中的一个描述子，分别计算与第二副图片每个描述子的汉明距离，然后选取最近的距离以及所对应的匹配对，然后多次选取图片1中的描述子重复上述操作，分别找到最短距离和相应的匹配对。最后再将比较得到的最小距离与设定的经验阈值作比较，如果小于经验阈值则保留并输出该匹配对。

参考链接：

（1）视觉SLAM ch7代码总结（一）_雨幕丶的博客-CSDN博客

（2）ORB特征匹配、手写ORB特征代码详解 - 知乎

（3）《视觉SLAM十四讲》-7.2 手写ORB特征_BetterTL的博客-CSDN博客_手写orb特征

（4）特征描述子匹配公用接口 — OpenCV 2.3.2 documentation