Influence Maximization across Partially Aligned Heterogenous Social Networks
部分对齐的异构社交网络的影响力最大化
- 前言
- 文章内容
-
- 摘要
- 背景
-
- AHI问题与其他影响力最大化问题的不同之处:
- AHI的挑战:
- 问题定义
- 提出的模型
-
- 多对齐多关系网络提取
- 多对齐多关系网络中的影响传播
-
- 传统的线性阈值模型(Linear threshold)
- 改进的线性阈值模型
- M&M模型中的影响最大化问题
-
- 分析一下
- AHI问题的贪婪算法
- 实验
-
- 数据集
前言
PAKDD2015年的文章,最早一批人研究异质信息网络中影响力最大化的成果吧。但是研究的异质信息网络只有关系的异质性。

https://link.springer.com/chapter/10.1007/978-3-319-18038-0_5
文章内容
摘要
The influence maximization problem aims at finding a subsetof seed users who can maximize the spread of influence in online socialnetworks (OSNs). Existing works mostly focus on one single homogenousnetwork. However, in the real world, OSNs (1) are usually heterogeneous,via which users can influence each others in multiple channels; and (2)share common users, via whom information could propagate across networks.
In this paper, for the first time we study the influence maximizationproblem in multiple partially aligned heterogenous OSNs. A new model,multi-aligned multi-relational network influence maximizer (M&M), isproposed to address this problem. M&M extracts multi-aligned multi-relational networks (MMNs) from aligned heterogeneous OSNs basedon a set of inter and intra network social meta paths. Besides, M&Mextends traditional linear threshold (LT) model to depict the information diffusion across MMNs. In addition, M&M, which selects seed usersgreedily, is proved to achieve a ( 1 − 1 / e ) (1-1/e) (1−1/e)-approximation of the optimalsolution. Extensive experiments conducted on two real-world partiallyaligned heterogeneous OSNs demonstrate its effectiveness.
影响力最大化问题的目标是找到能够最大化在线社交网络(OSN)中影响力传播的种子用户。现有的工作主要集中在一个单一的同质网络上。然而,在现实世界中,OSN(1)通常是异构的,用户可以通过它在多个渠道中相互影响;以及(2)共享共同用户,信息可以通过这些用户在网络上传播。
在本文中,我们首次研究了多个部分对齐的异质OSN中的影响最大化问题。为了解决这一问题,提出了一种新的模型,多对齐多关系网络影响最大化器(M&M)。M&M基于一组网络间和网络内社交元路径从对齐的异构OSN中提取多对齐的多关系网络(MMNs)。此外,M&M扩展了传统的线性阈值(LT)模型来描述MMNs中的信息扩散。此外,自由选择种子用户的M&M被证明实现了 ( 1 − 1 / e ) (1-1/e) (1−1/e)-最优解的近似。在两个真实世界部分对齐的异构OSN上进行的大量实验证明了其有效性。
背景
用户常同时参加多个社交网络,跨多个社交网络的共享用户被称为anchor user(锚点用户)。锚点用户的存在使得影响力不仅可以在社交网络内传播,也可以在社交网络之间传播。
我觉得这里的锚点用户也相当于社交网络社区之间的桥连用户。
 两幅图是一些与跨社交网络用户行为的分析。图(a)中,从Foursquare随机抽取500人,其中409人会转发活动到Twitter,但图(b)表示这409人的转发活动仅仅占他们在Foursquare中总活动的一小部分。所以作者认为锚点用户不会将其所有信息传播到另一个网络。
两幅图是一些与跨社交网络用户行为的分析。图(a)中,从Foursquare随机抽取500人,其中409人会转发活动到Twitter,但图(b)表示这409人的转发活动仅仅占他们在Foursquare中总活动的一小部分。所以作者认为锚点用户不会将其所有信息传播到另一个网络。
提出了对齐异构网络影响力最大化问题:
Aligned Heterogeneous network Influence maxmization(AHI) problem
关于锚点用户,作者给出了一些图来解释
 图A显示了两个部分对齐的异构输入网络。
图A显示了两个部分对齐的异构输入网络。
图B是提取多关系,基于构建的多关系网络选择最佳的种子用户集合。
图C是传统的单一同质社交网络中的病毒营销。
图D是单个多关系网络中的信息扩散。
图E是多重社交网络的影响力最大化,跨多个单一同质网络。
AHI问题与其他影响力最大化问题的不同之处:
- 社交网络是异质的;
- 同时研究了多个社交网络,其中不同的异构网络可能具有不同的结构或者网络模式;
- 研究了社交网络是通过锚点用户部分对齐的,并不是简单合并在一起。
AHI的挑战:
- 异构网络中测信息扩散,关系的多样性,如何建模网络中的信息传播?
- 跨网络信息传播:信息可以通过锚点用户传播,如何建模网络间的信息扩散?
- NP难问题,效率问题。
针对这些问题,提出了Multi-aligned Multi-relational network influence maximizer(M&M)model
多对齐多关系网络影响力最大化模型。
- 首先基于一组网络间和网络内的远路径,通过输入OSN中的异构信息来构建多对齐多关系网络。
- 扩展了传统的线性阈值(LT)模型,以描述多对齐多关系网络内部和之前的信息传播。(证明了单调性和子模性)
- 利用贪心算法,可以实现 ( 1 − 1 / e ) (1-1/e) (1−1/e)
问题定义
AHI问题定义:
给定两个部分对齐网络 G ( 1 ) G^{(1)} G(1)和 G ( 2 ) G^{(2)} G(2),还有 G ( 1 ) G^{(1)} G(1)和 G ( 2 ) G^{(2)} G(2)之间的无向锚链接集 A \mathcal A A, U ( 1 ) \mathcal U^{(1)} U(1)和 U ( 1 ) \mathcal U^{(1)} U(1)分别表示 G ( 1 ) G^{(1)} G(1)和 G ( 2 ) G^{(2)} G(2)的用户节点集。设 σ ( ⋅ ) : Z → R \sigma(·): \mathcal Z\rightarrow\mathbb{R} σ(⋅):Z→R, Z ⊂ U ( 1 ) ∪ U ( 2 ) \mathcal Z\subset\mathcal U^{(1)}\cup\mathcal U^{(2)} Z⊂U(1)∪U(2), σ ( ⋅ ) \sigma(·) σ(⋅)是影响函数,将种子用户集合 Z \mathcal Z Z映射到受 Z \mathcal Z Z影响的用户数量。AHI问题旨在选择包含 d d d个种子的最优集合 Z ∗ \mathcal Z* Z∗来使影响扩散最大化。
提出的模型
多对齐多关系网络提取
基于网络模式(network schema)定义的元路径来提取有异构信息的多对齐多关系网络。
1.网络模式的定义:给定网络 G G G,其网络模式为 S G = ( O , R ) S_{G}=(O,R) SG=(O,R), O , R O,R O,R分别表示 G G G中的节点类型和连接类型。
不同网络的网络模式不同,所以不能简单合并在一起。基于网络模式,将传播渠道表示为一组网络内和网络间的社交元路径。
2.网络内社交元路径的定义:
基于给定的网络模式 S G = ( O , R ) S_{G}=(O,R) SG=(O,R),定义网络内社交元路径 P = O 1 → R 1 O 2 → R 2 ⋯ → R k − 1 O k ( k > 1 ) \mathcal P=O_1\xrightarrow{R_1}O_2\xrightarrow{R_2}\dots\xrightarrow{R_{k-1}}O_{k}(k>1) P=O1R1O2R2⋯Rk−1Ok(k>1),其中 O i ∈ O , i ∈ { 1 , 2 , … , k } , R i ∈ R , i ∈ { 1 , 2 , … , k − 1 } O_i\in O, i\in\{1,2,\dots,k\}, R_i\in R, i\in\{1,2,\dots,k-1\} Oi∈O,i∈{1,2,…,k},Ri∈R,i∈{1,2,…,k−1}。本文主要关注的元路径是连接用户的 O 1 … O k = U s e r ∈ O O_1\dots O_k=User\in O O1…Ok=User∈O,即社交元路径。
3.网络间社交元路径的定义:两个部分对齐的异质信息网络 G ( 1 ) G^{(1)} G(1)和 G ( 2 ) G^{(2)} G(2),分别有网络模式 S G ( 1 ) = ( O ( 1 ) , R ( 1 ) ) S_{G^{(1)}}=(O^{(1)},R^{(1)}) SG(1)=(O(1),R(1))和 S G ( 2 ) = ( O ( 2 ) , R ( 2 ) ) S_{G^{(2)}}=(O^{(2)},R^{(2)}) SG(2)=(O(2),R(2))。定义网络间的网络模式 Q = O 1 → R 1 O 2 → R 2 ⋯ → R k − 1 O k ( k > 1 ) \mathcal Q=O_1\xrightarrow{R_1}O_2\xrightarrow{R_2}\cdots\xrightarrow{R_{k-1}}O_{k}(k>1) Q=O1R1O2R2⋯Rk−1Ok(k>1),其中 O i ∈ O ( 1 ) ∪ O ( 2 ) , i ∈ { 1 , 2 , … , k } , R i ∈ R ( 1 ) ∪ R ( 2 ) ∪ { A n c h o r } , i ∈ { 1 , 2 , … , k − 1 } O_i\in O^{(1)}\cup O^{(2)}, i\in\{1,2,\dots,k\}, R_i\in R^{(1)} \cup R^{(2)}\cup \{Anchor\}, i\in\{1,2,\dots,k-1\} Oi∈O(1)∪O(2),i∈{1,2,…,k},Ri∈R(1)∪R(2)∪{Anchor},i∈{1,2,…,k−1}, A n c h o r Anchor Anchor是锚链接类型。并且, O 1 = U s e r ∈ O ( 1 ) O_1=User \in O^{(1)} O1=User∈O(1), O k = U s e r ∈ O ( 2 ) O_k=User \in O^{(2)} Ok=User∈O(2),表示元路径的两端在不同的网络中, ∃ m ∈ { 1 , 2 , … , k − 1 } \exists m\in \{1,2,\dots, k-1\} ∃m∈{1,2,…,k−1}使得 R m = { A n c h o r } R_m=\{Anchor\} Rm={Anchor},也就是元路径的关系中一定存在锚连接。
根据Foursquare和Twitter的特性,设计元路径:
-
Foursquare网络内的社交元路径:
1. f o l l o w : U s e r → f o l l o w − 1 U s e r follow:User\xrightarrow{follow^{-1}}User follow:Userfollow−1User
2. c o − l o c a t i o n c h e c k i n s : U s e r → c h e c k i n L o c a t i o n → c h e c k − 1 U s e r co-location checkins:User\xrightarrow{checkin}Location\xrightarrow{check^{-1}}User co−locationcheckins:UsercheckinLocationcheck−1User
3. c o − l o c a t i o n v i a s h a r e d l i s t s : U s e r → c r e a t e / l i k e L i s t → c o n t a i n L o c a t i o n → c o n t a i n − 1 L i s t → c r e a t e / l i k e − 1 U s e r co-location via shared lists:User\xrightarrow{create/like}List\xrightarrow{contain}Location\xrightarrow{contain^{-1}}List\xrightarrow{create/like^{-1}}User co−locationviasharedlists:Usercreate/likeListcontainLocationcontain−1Listcreate/like−1User -
Twitter网络内的社交元路径:
1. f o l l o w : U s e r → f o l l o w − 1 U s e r follow:User\xrightarrow{follow^{-1}}User follow:Userfollow−1User
2. c o − l o c a t i o n c h e c k i n s : U s e r → c h e c k i n L o c a t i o n → c h e c k − 1 U s e r co-location checkins:User\xrightarrow{checkin}Location\xrightarrow{check^{-1}}User co−locationcheckins:UsercheckinLocationcheck−1User
3. c o n t a c t v i a t w e e t : U s e r → w r i t e T w e e t → r e t w e e t T w e e t → w r i t e − 1 U s e s r contact via tweet:User\xrightarrow{write}Tweet\xrightarrow{retweet}Tweet\xrightarrow{write^{-1}}Usesr contactviatweet:UserwriteTweetretweetTweetwrite−1Usesr -
跨网络元路径:
U s e r → A n c h o r U s e r User\xrightarrow{Anchor}User UserAnchorUser
由于跨网络元路径,使两个网络中的非锚点用户也可以通过网络内和网络间元路径相连,元路径实例数量变得很多。
4.多对齐多关系网络的定义:
给定两个异质信息网络 G ( 1 ) G^{(1)} G(1)和 G ( 2 ) G^{(2)} G(2),定义多对齐多关系网络MMNs,公式化 M = ( U , E , R ) M=(U,E,R) M=(U,E,R),其中 U = U ( 1 ) ∪ U ( 2 ) U=U^{(1)}\cup U^{(2)} U=U(1)∪U(2)表示网络中的节点,集合 E E E是节点 U U U之间的链接集。元素 e = ( u , v , r ) ∈ E e=(u,v,r)\in E e=(u,v,r)∈E表示 ( u , v ) (u,v) (u,v)之间至少存在一种连接类型 r ∈ R = R ( 1 ) ∪ R ( 2 ) ∪ { A n c h o r } r\in R=R^{(1)}\cup R^{(2)} \cup \{Anchor\} r∈R=R(1)∪R(2)∪{Anchor}, R ( 1 ) R^{(1)} R(1)和 R ( 2 ) R^{(2)} R(2)表示两个网络内部的链接关系, A n c h o r Anchor Anchor表示两个网络之间的链接关系。
多对齐多关系网络中的影响传播
传统的线性阈值模型(Linear threshold)
在单一同质网络 G = ( V , E ) G=(V,E) G=(V,E),用户 u i ∈ V u_i\in V ui∈V可以影响他的邻居 u k ∈ Γ i n ( u i ) ⊆ V u_k\in \varGamma_{in}(u_i)\subseteq V uk∈Γin(ui)⊆V,影响权重是 w i , k ⩾ 0 w_{i,k}\geqslant 0 wi,k⩾0,如果 u i u_i ui是非活跃态则 w i , k = 0 w_{i,k}=0 wi,k=0,
Γ i n ( u i ) \varGamma_{in}(u_i) Γin(ui)表示follow了 u i u_i ui的用户,并且 ∑ u k ∈ Γ i n ( u i ) w i , k ≤ 1 \sum_{u_k\in \varGamma_{in}(u_i)}w_{i,k}\leq 1 ∑uk∈Γin(ui)wi,k≤1。每个节点,例如 u i u_i ui都有一个静态阈值 θ i \theta_i θi,表示激活所需的最小影响。影响力以离散步传播,已经被激活的节点保持活跃,非激活态的节点如果接收到了超过阈值的影响力则可以被激活。只有在t步被激活的节点才能在t+1步去影响它的邻居。
在MMNs中 M = ( U , E , R ) M=(U,E,R) M=(U,E,R),由pathsim来估计不同扩散的权重
-
网络内部的扩散权重
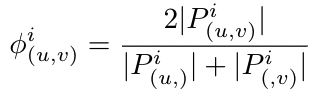
u , v u,v u,v是用户, i i i是关系。 P ( u , v ) i P_{(u,v)}^i P(u,v)i表示从 u u u开始到 v v v结尾,关系为 i i i的网络内元路径实例集合。 ∣ ⋅ ∣ |·| ∣⋅∣是集合的大小。 P ( u , ) i P_{(u,)}^i P(u,)i和 P ( , v ) i P_{(,v)}^i P(,v)i分别是 u , v u,v u,v作为起始和中止节点的元路径实例。 -
网络之间的扩散权重

u , v u,v u,v是用户, j j j是关系。 Q ( u , v ) j Q_{(u,v)}^j Q(u,v)j表示从 u u u开始到 v v v结尾,关系为 i i i的网络之间元路径实例集合。 ∣ ⋅ ∣ |·| ∣⋅∣是集合的大小。 Q ( u , ) j Q_{(u,)}^j Q(u,)j和 Q ( , v ) j Q_{(,v)}^j Q(,v)j分别是 u , v u,v u,v作为起始和中止节点的元路径实例。
改进的线性阈值模型
一个网络中的用户 v v v被激活的概率根据网络内部的联系 i i i和网络之间的联系 j j j,分别表示为:
- 网络内部的
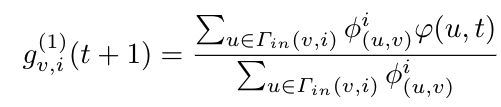
- 网络之间的
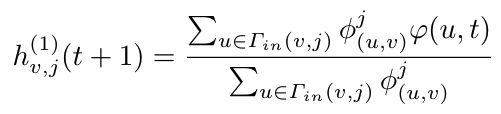
Γ i n ( v , i ) \varGamma_{in}(v,i) Γin(v,i)和 Γ i n ( v , j ) \varGamma_{in}(v,j) Γin(v,j)是用户 u u u以关系 i , j i,j i,j相连的邻居。
φ ( u , t ) \varphi(u,t) φ(u,t)表示节点 u u u在时间 t t t是否被激活。
注意,锚用户用户 v ( 1 ) v^{(1)} v(1)被激活并不代表 v ( 2 ) v^{(2)} v(2)同时被激活,但是 v ( 2 ) v^{(2)} v(2)可以通过锚链接从 v ( 1 ) v^{(1)} v(1)获取影响力。
得到 v v v的综合的激活概率,使用logistic函数作为聚合函数。

ρ i ( 1 ) \rho_i^{(1)} ρi(1)和 ω j ( 1 ) \omega_j^{(1)} ωj(1)表示扩散过程中每个关系的权重,其值满足 ∑ ( i ) ρ i ( 1 ) + ∑ ( j ) ω j ( 1 ) = 1 , ρ i ( 1 ) ≥ 0 , ω j ( 1 ) ≥ 0 \sum_{(i)}\rho_i^{(1)}+\sum_{(j)}\omega_j^{(1)}=1,\rho_i^{(1)}\geq 0, \omega_j^{(1)}\geq 0 ∑(i)ρi(1)+∑(j)ωj(1)=1,ρi(1)≥0,ωj(1)≥0。同样的,在 G ( 2 ) G^{(2)} G(2)中 v ( 2 ) v^{(2)} v(2)的激活概率也是一样计算。
M&M模型中的影响最大化问题
分析一下
传统的影响力最大化问题对于LT模型是NP难的,影响函数是单调和子模的,基于此,贪婪算法的近似比为 1 − 1 / e 1-1/e 1−1/e。
需要证明M&M模型下的影响力最大化问题也是NP难,影响扩散函数也是单调且子模的
- 定理1:跨部分对齐的异质社会网络(AHI)的影响最大化问题是NP难题。
证明:AHI问题可以很容易地映射到NP完全的“顶点覆盖”问题。因此AHI问题是NP难的。
- 定理2:对于M&M模型,影响函数 σ ( Z ) \sigma(\mathcal Z) σ(Z)是单调的。
证明:给定现有的种子用户集合 Z \mathcal Z Z,让 z z z称为本轮选择的种子用户。由于多关系的权重是非负的,添加一个新的种子用户 z z z不会减少受影响用户的数量,即 σ ( Z + z ) ≥ σ ( Z ) \sigma(\mathcal Z+z)\geq\sigma(\mathcal Z) σ(Z+z)≥σ(Z)。因此,对于给定的M&M模型,影响扩散函数是单调的。
-定理3:对于M&M模型,影响函数 σ ( Z ) \sigma(\mathcal Z) σ(Z)是子模的。
证明:可以用[12]中提出的活边路径方法来证明。
[12]D. Kempe, J. Kleinberg, and ́E. Tardos. Maximizing the spread of influence througha social network. InKDD, 2003.
AHI问题的贪婪算法
- 输入:两个网络 G ( 1 ) G^{(1)} G(1)和 G ( 1 ) G^{(1)} G(1),锚用户矩阵 A n ( 1 ) × n ( 2 ) A_{n_{(1)}\times n_{(2)}} An(1)×n(2),种子节点个数d
- 输出:种子节点集 Z Z Z
- line 1:初始化种子集合 Z = [ ] Z=[] Z=[],种子索引 i = 0 i=0 i=0
- line 2:获取两个网络的网络模式 S G ( 1 ) S_G^{(1)} SG(1)和 S G ( 2 ) S_G^{(2)} SG(2),用户节点集合 U = U ( 1 ) ∪ U ( 2 ) U=U^{(1)}\cup U^{(2)} U=U(1)∪U(2)
- line3-5:对于节点集中的每一个节点v,提取它网络内和网络间的扩散元路径。
- line 6:计算关系的扩散强度 ϕ ( u , v ) \phi_{(u,v)} ϕ(u,v)和 ψ ( u , v ) \psi_{(u,v)} ψ(u,v)
- line 7: 定义激活概率向量 P ( 1 ) P^{(1)} P(1)和 P ( 2 ) P^{(2)} P(2),并计算初始值(激活概率是p,向量用P)
- line 8:进入循环并在选出 d d d个节点之后结束循环
- line 9-11:对于每一个不在 Z Z Z中的节点 u u u,用蒙特卡洛方法基于激活概率计算边际收益 M u = σ ( Z ∪ { u } ) − σ ( Z ) M_u=\sigma(Z\cup\{u\})-\sigma(Z) Mu=σ(Z∪{u})−σ(Z),
- line 12-13:选取 M u M_u Mu最大的节点,并加入种子集合 Z Z Z
- line 14: 更新激活概率向量 P ( 1 ) P^{(1)} P(1)和 P ( 2 ) P^{(2)} P(2),种子索引 i = i + 1 i=i+1 i=i+1

