三维坐标变换矩阵的推导过程

三维坐标变换矩阵的推导过程

在3D计算机图形学中，我们经常需要使用多个坐标系，因此我们需要知道如何从一个坐标系转到另一个坐标系。在3D计算机图形学中，点(Point)和向量(Vector)的变换是不同的，所以需要分别讨论。

1、向量的变换

 

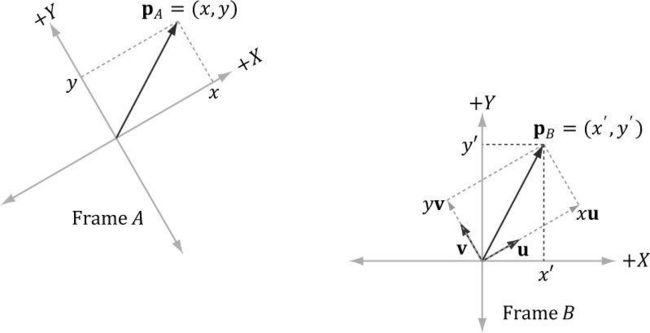
如图所示，有两个坐标系A、B和一个向量p。假设我们已经知道了p在坐标系A下的坐标为pA = (x,y);现在我们要求p在坐标系B下的坐标，pB = (x',y') 。也就是说，给定一个坐标系下的向量p，如何计算p在另一个坐标系下的坐标呢？

显然，在坐标系A下，p = x*u + y*v;其中u、v为坐标系A下沿着x轴和y轴的单位向量；而在坐标系B下，p = x*uB + y*vB ，其中uB和vB为A坐标系下的x轴和y轴在B坐标系下的向量表示。因此，如果求出uB = (ux,uy),vB = (vx,vy),则可以求出pB = (x',y')的值。

相应地，将二维情况推广到三维，即可得到：

如果向量pA = (x , y , z),则pB = x*uB + y*vB + z*wB;其中pA为p在A坐标系下的向量表示，pB为p在B坐标系下的向量表示，uB 、vB 、wB分别为A坐标系下的坐标轴x、y、z在B坐标系下的向量表示。

2、点的变换

 

 

 

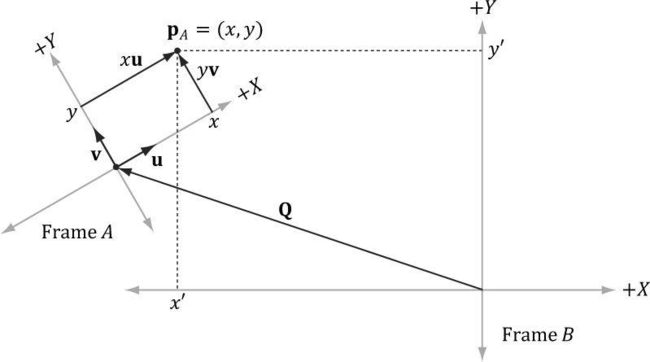
点是需要包含位置信息的，因此，点的变换和向量的变换稍微有些不同。

如图所示，在坐标系A下，点p可表示为：p = x*u + y*v + Q ，其中u、v为坐标系A的坐标轴，Q为坐标系A原点的坐标。而在B坐标系下，点p可表示为:p = x*uB + y*vB + QB ,其中uB和vB为A坐标系下的x轴和y轴在B坐标系下的向量表示，QB为A坐标系下的原点在B坐标系下的坐标表示。因此，我们只要求出uB = (ux,uy),vB = (vx,vy),QB = (Qx,Qy),则可求出点p在B坐标下的坐标表示。

同理，将上述变换推广到三维可得：

如果点pA = (x , y , z),则点pB = x*uB + y*vB + z*wB +QB ;其中pA为p在A坐标系下的坐标，pB为p在B坐标系下的坐标，uB 、vB 、wB分别为A坐标系下的坐标轴x、y、z在B坐标系下的向量表示，QB为A坐标系下的原点在B坐标系下的坐标表示。

 

3、点和向量的矩阵表示

结合1和2可得，

对于向量：

(x', y', z') = x*uB + y*vB + z*wB;

对于点:

(x', y', z') = x*uB + y*vB + z*wB + QB。

使用齐次坐标，我们将以上两式统一表示为：

(x', y', z',w') = x*uB + y*vB + z*wB + w*QB。

 其中，w=0，为向量的坐标变换；w=1，为点的坐标变换。
 

令QB = (Qx ,Qy ,Qz ,1), uB = (ux , uy , uz ,0), vB = (vx ,vy ,vz ,0), wB = (wx , wy , wz ,0)，则可得坐标系A到坐标系的变换矩阵为