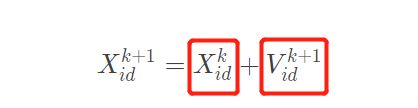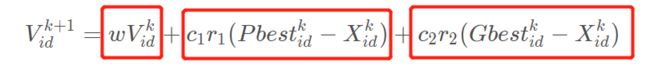进化算法之粒子群算法介绍附代码——PSO
粒子群算法PSO
- 背景介绍
-
- 算法介绍
- 鸟群觅食
- 算法&鸟群
-
- 重点
- 算法介绍
-
- 简单概念
- 大致流程
-
- 核心流程
- 核心公式
-
- 公式拆解
- 算法的伪代码
- PSO的应用场景
背景介绍
算法介绍
粒子群算法,英文全称为Partricle Swarm Optimization,所以简称为PSO算法,它是一种基于群体协作的随机搜索算法,个人理解是PSO算法是属于迭代性质的进化算法,也就是说下一个结果是基于上一个结果所传递的信息,并更新后的结果。PSO算法是基于鸟群觅食的行为所提出来的算法。所以在了解PSO算法需要了解鸟群是如何觅食的。一种基于群体协作的随机搜索算法
鸟群觅食
故事一:
假设有若干个食物分别藏在一片大森林中,此时有一群鸟想要去寻找这些食物,可是他们并不知道食物的具体位置,但是他们会感应到食物的大概位置。那么在它们的感应范围内,离食物最近的小鸟就会将自己的位置信息广播出去,(或者是传递出去),然后整个鸟群就会改变他们的飞行方向,改变后的方向就是将自己的位置信息广播出去的小鸟,以他们的速度飞过去 ,然后不断重复,直到他们找到食物为止。
故事二:
有一天森林飞来了一群鸟儿,由于长时间的飞行让每一个鸟儿饿死了快。所以它们进入森林第一件事就是寻找食物,但是因为鸟儿们第一次在这个森林中展开合作,所以它们并不知道哪里可以找得到食物,于是每个鸟儿就抱着天涯未远,江湖再见,后会有期的想法,决定每一个都朝着不同的方向独自寻找,开始大范围的捕食行为。
但是为了能够更快的找到虫子吃,它们在出发前就立了一个投名状,要是谁发现了虫子,就喊一嗓子。
随着时间的流逝,终于有一个鸟儿——小烨,它似乎发现在它附近不远处有食物的踪迹。于是它开始传话给它的兄弟们,那么小烨的兄弟在收到消息后,便开始改变轨迹,都往小烨那边。此时小烨在自己的感知范围内搜小范围圈继续寻找虫子。最终,随着小烨越来越接近虫子。其他兄弟也差不多都聚集到了小烨这边。最终,大家都吃到了食物。
算法&鸟群
鸟群觅食的行为正是这个粒子群算法被提出的原因。因此,如果想更好的了解粒子群算法,我们就要来分析故事二。首先,我们来分析分析鸟宝宝们的运动状态,即每一个鸟儿是怎么决定自身的飞翔速度和位置的。
- 首先,大家都知道的道理就是——物体是具有惯性的,如此说来鸟儿在一开始飞翔的时候,无论它下一次想怎么飞,往哪个方向飞,都是有一个惯性存在的,所以它必须根据当前的速度和方向来进行下一步的调整。对吧,这个应该可以理解的吧?因此,“惯性” ——当前的速度是一个因素。
- 其次,由于鸟群长期捕食,因此每一只鸟儿是有经验的,它虽然不知道具体哪里是有食物的存在,但是它能大概知道食物分布在哪里。比如当鸟儿飞到荒不拉几的一个地方,根据经验,它肯定知道这里是不会有虫子的,但是它到一个大森林里,它肯定知道这里面是有食物的。因此,在鸟儿的心中,在寻找食物的过程中它每次飞,都会根据自己的经验来找,比如以往食物分布的地区,它肯定优先对这部分的地方进行搜索。因此,个人认知——也是一个因素。(也可以理解为经验)
- 最后,每个鸟儿发现自己离虫子非常接近的时候,便会发出信号给同伴,在遇到这样的信号,其余还在找的鸟儿们就会想着,兄弟的位置更接近虫子,我得上它那看看去。这样的信息沟通,我们称之为“社会共享”,这也是鸟群在移动时考虑的一个因素——社会共享。
综上所述,鸟儿每次在决定下一步移动的速度和方向时,脑子里是由这三个因素(速度,个人认知——经验,社会认知——信息)影响的。我们想,如果能够用一条公式来描述着三个因素的影响的话,那不就能写出每个鸟儿的移动方向和速度么。但是,每一个鸟儿,对这三个因素的考虑都是不一致的,比如对于捕食经验不高的鸟宝宝,移动的时候会更看重同伴分享的信息,而对于捕食经验高的鸟大叔,则更看重自己的经验。因此,我们的公式,在“个人认知”和“社会共享”这部分,是具有随机性的。
重点
PSO算法就是把鸟群中每一只鸟儿比作没有质量和体积的粒子,粒子成为利用算法去求解优化问题时候的每一个潜在的解(注意这里是一个粒子对应的一个潜在解),那么鸟群们找到的食物就是最优解。结合上述故事,就是在说鸟儿们捕食的过程,也就是所有的粒子在解空间内寻找到最优解的过程。
每一个粒子,都由一个适应度函数来确定适应度,以此来确定粒子位置的好坏。适应度函数其实就是模仿鸟儿的“经验”判断部分,通过适应度函数来确定这个位置是不是所谓的贫瘠地或是虫子可能出现的位置。
注:这里的适应度和适应度函数什么,后面有介绍, 因为内容设计问题,这里没法展开介绍,大家记住这个名词即可,谨记这个适应度很重要
每一个粒子被赋予了记忆功能,能够记忆所搜寻过的最佳位置。
每一个粒子都有一个速度以及决定飞行的距离和方向,这个根据它本身的飞行经验和同伴共享的信息所决定。
算法介绍
粒子群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解
简单概念
为了方便大家理解,我在解释概念时以二维向量为例,并附上一个GIF更容易理解
- 粒子——优化问题的潜在解,也可以叫做候选解。
eg:假设在一个二维优化问题,那么二维的每一个向量[x1 ,x2]… …[xa ,xb]为每一个粒子,粒子们便构成了粒子群。
- 位置——粒子(候选解)的位置
eg:二维向量[x1 x2]… …[xa xb]都是有一定的数值,占据着二维空间中一个点的位置。
- 速度——粒子(候选解)移动的速度
eg:每一个二维向量向下一个位置的移动速度
- 适应度——fitness value,评价粒子的优劣值,一般为优化目标的函数值
- 适应度函数——fitness function,适应度函数确定适应度
eg:假设函数为
y = f ( x a , x b ) = x a 2 + x b 2 y=f(x_a,x_b)=x_a^{2}+x_b^{2} y=f(xa,xb)=xa2+xb2
y代表每一个粒子的值,通过比较y来评价粒子的优劣,那么对于这个函数来说,y值越小,粒子越接近极值,粒子越好。
- 个体极值——Pbest,单个粒子在所经历的所有位置中,计算得到的适应度值最优位置
针对上述粒子的函数y,假设一个粒子第一个位置[3 ,5],第二个位置是[2 ,5],第三个位置[5 ,5],显而易见第二个位置是最接近极值,所有说第二位置[2 ,5]为个人极值
- 群体极值——Gbest,种群中的所有粒子搜索到的适应度最优值
群体极值不仅要比较每一个粒子的历史极值,还要与所有的粒子,也就是粒子群综合比较
GIF解释
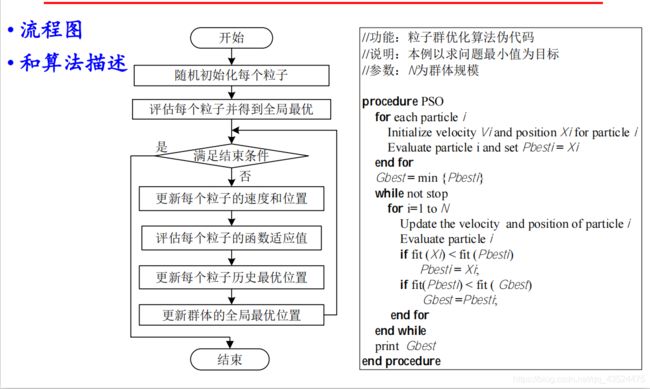
大致流程
核心流程
- 初始化粒子:在求解空间内随机产生初始化粒子,以及初始化粒子的速度
注意:有些同学会问:既然是粒子把鸟儿抽象化,那粒子的初始化为什么只初始化速度,不初始化方向呢,大家注意PSO算法的粒子,在一个N维空间内,粒子是一个N维向量,既然是向量,那么粒子就一定是具有方向的,因为向量本身是既具有粒子,也具有方向的。所以在粒子的初始化中,初始化粒子的速度,也相当于初始化粒子的方向。
- 计算适应度:根据适应度函数计算当前粒子的适应度值(把每一个粒子代入到适应度函数里计算值)然后寻找群体的最优值。
简单化就是说将xi带入适应函数f(xi)求适应值
- 更新粒子的速度与位置: 粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置,粒子每更新一次位置,就计算一次适应度值,并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。
核心公式
速度更新公式和位置更新公式是PSO算法中的核心公式
速度更新公式:
V i d k + 1 = w V i d k + c 1 r 1 ( P b e s t i d k − X i d k ) + c 2 r 2 ( G b e s t i d k − X i d k ) V_{id}^{k+1}=wV_{id}^{k}+c_1r_1(Pbest_{id}^{k}-X_{id}^{k})+c_2r_2(Gbest_{id}^{k}-X_{id}^{k}) Vidk+1=wVidk+c1r1(Pbestidk−Xidk)+c2r2(Gbestidk−Xidk)
位置更新公式:
X i d k + 1 = X i d k + V i d k + 1 X_{id}^{k+1}=X_{id}^{k}+V_{id}^{k+1} Xidk+1=Xidk+Vidk+1
上标k1和k+1表示粒子从k次飞行操作到下一次飞行操作的过程
公式拆解
- 首先我们需要只要,两个公式里面每一个字母含意是什么
Xid:表示为粒子i的位置,即Xi=(Xi1,Xi2,…,Xid)
Vid:表示为粒子i的速度,即Vi=(Vi1,Vi2,…,Vid)
有些同学会问,为什么会存在下标i1,i2,…,id呢,不要忘记,PSO算法是一个始终迭代,始终更新的一个过程。
通常,在第d(1<=d<=D)维内,我们要给我们的粒子速度和位置做一个限制,毕竟我们不希望鸟儿的速度过快或者以及飞出我们要搜寻的范围。因此对于每个粒子i,有:
X i ∈ [ X m i n , X m a x ] X_i∈[X_{min},X_{max}] Xi∈[Xmin,Xmax]
V i ∈ [ V m i n , V m a x ] V_i∈[V_{min},V_{max}] Vi∈[Vmin,Vmax]
Pbestid:表示为粒子i所搜寻到的最好的位置,即Pbesti=(Pbesti1,Pbesti2,…,Pestid)
Gbestid:表示为种群所搜寻到的最好的位置,即Bbesti=BPbesti1,Bbesti2,…,Bestid)
w:表示为惯性权重,是用于调节对解空间的搜索范围
惯性权重w是一个很重要的参数,其值越大,全局搜索能力更强,前提有比较大的全局搜索能力,但在后期可能会错过最优值。其值越小,局部搜索能力更强,但也可能就此找不到全局的最优解,目前惯性权重应该如何取值,很多世界级的大佬们都在研究
所以说惯性权重并不是一个固定值,动态w能获得比固定值更好的寻优结果,一般来说,惯性权值取值为0.9,0.4时算法性能最好。就开始先用较大的惯性权重去满足全局搜索能力,后用较小的惯性权重去满足局部搜索能力。
c1和c2是学习因子,表示我们自己对给“个人认知”和“社会共享”这两部分的分量的控制;

r1、r2是随机数, 给“个人认知”和“社会共享”提供随机性,即每个粒子对这两部分的看重是不一样的。一般的取值范围是[0-1]。
在公式里,个人认知 表示为 速度更新公式“+”号的第二部分,社会共享表示为“+”号的第三部分
位置公式:可以分为两个部分
- 第一个红方框表示的为粒子上一次的位置。
- 第二个红方框表示为粒子下一次的速度。
我们都知道一个物理知识就是x=x0+vt。即新位置=初始位置+速度时间,可是这里为什么少了个t呢,这里我们可以简单理解为从k飞行到k+1飞行,耗费了一个单位时间t,因此就没有t出现了。
速度更新公式:可以分为三个部分,不难发现的是这三个部分,正是我们前面分析的“惯性”、“个人认知”、“社会共享”这三大块。
- 第一个红方框,表示k次速度大小和方向的影响;其中惯性权重w体现的是粒子继承先前的速度的能力。
- 第二个红方框,表示是从当前点指向粒子自身最好点的一个矢量,表示粒子的动作来源于自己经验的部分;
- 第三个红方框,表示是一个从当前点指向种群最好点的矢量,反映了粒子间的协同合作和知识共享。
所以根据速度更新公式,我们不难发现的是,粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
算法的伪代码
PSO的应用场景
PSO具有很大的发展价值和发展空间,算法能够用于多个领域并创造价值,在群智能算法中具有重要的地位,同时也能够在相关产业创造价值,发挥作用。下面结合相关产业具体分析一下。
计算智能的算法,往往结合大数据平台,包括GPU运算,并行计算,HPC,多模式结合等手段,来完成更加复杂多变的业务需求。
下面具体分析在产业中的作用:
- 模式识别和图像处理。PSO算法已在图像分割、图像配准、图像融合、图像识别、图像压缩和图像合成等方面发挥作用。
- 神经网络训练。PSO算法可完成人工神经网络中的连接权值的训练、结构设计、学习规则调整、特征选择、连接权值的初始化和规则提取等。但是速度没有梯度下降优化的好,需要较大的计算资源。一般都算不动。
- 电力系统设计,例如:日本的Fuji电力公司的研究人员将电力企业某个著名的RPVC(Reactive Power and Voltage Control)问题简化为函数的最小值问题,并使用改进的PSO算法进行优化求解。
- 半导体器件综合,半导体器件综合是在给定的搜索空间内根据期望得到的器件特性来得到相应的设计参数。
- 还有其他的一些相关产业。包括自动目标检测、生物信号识别、决策调度、系统识别以及游戏训练等方面也取得了一定的研究成果。
PSO算法代码,请移步 - PSO算法代码详解
参考文章:
-
粒子群优化 PSO-Particle Swarm Optimization
-
最优化算法之粒子群算法(PSO)
-
数学建模——粒子群算法(PSO)
-
粒子群优化算法(PSO)简介及MATLAB实现
-
Qling的随笔