人工神经网络(ANN)及python实现
前言
初学人工智能不久,今天碰上了人工神经网(ANN),开始学的时候很懵,一大堆理论、公式、推导…作为一名小白,还是很痛苦的,不过经过摸索,大概了 解了什么是ANN,公式的推导以及一些其他问题,下面我就总结下自己的理解,一方面作为自己的笔记,日后方便巩固;另一方面,也可以分享给其他有意者。
一、什么是神经网络
1.单层神经网络
首先以单层神经元为例解释人工神经元是如何工作的
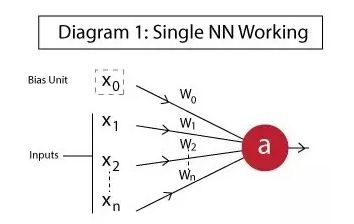
x1,x2,…, xN:神经元的输入。这些可以从输入层实际观测或者是一个隐藏层的中间值(隐藏层即介于输入与输出之间的所有节点组成的一层。后面讲到多层神经网络是会再跟大家解释的)。
X0:偏置单元。这是常值添加到激活函数的输入(类似数学里y=ax+b中使直线不过原点的常数b)。即截距项,通常有+1值。
w0,w1,w2,…,wN:对应每个输入的权重。甚至偏置单元也是有权重的。
a:神经元的输出。计算如下:
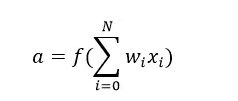
式子里的f是已知的激活函数,f使神经网络(单层乃至多层)非常灵活并且具有能估计复杂的非线性关系的能力。在简单情况下可以是一个高斯函数、逻辑函数、双曲线函数或者甚至上是一个线性函数。利用神经网络可让其实现三个基本功能:与、或、非(AND, OR, NOT)。
这里引入一个例子:and功能实现如下
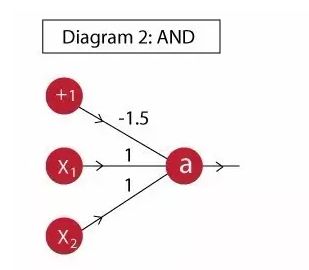
神经元输出:a = f( -1.5 + x1 + x2 )
这样大家就很容易理解其工作原理,其实就是对输入值赋予不同权重,经过激活函数输出的过程。
2.多层神经网络
2.1 网络结构
清楚了单层神经网络,多层神经网络也好理解了,就相当于多个单层的叠加成多层的过程。

神经网络分为三种类型的层:
输入层:神经网络最左边的一层,通过这些神经元输入需要训练观察的样本,即初始输入数据的一层。
隐藏层:介于输入与输出之间的所有节点组成的一层。帮助神经网络学习数据间的复杂关系,即对数据进行处理的层。
输出层:由前两层得到神经网络最后一层,即最后结果输出的一层。
2.2 传递函数/激活函数
前面每一层输入经过线性变换wx+b后还用到了sigmoid函数,在神经网络的结构中被称为传递函数或者激活函数。除了sigmoid,还有tanh、relu等别的激活函数。激活函数使线性的结果非线性化。
2.3 为什么需要传递函数
简单理解上,如果不加激活函数,无论多少层隐层,最终的结果还是原始输入的线性变化,这样一层隐层就可以达到结果,就没有多层感知器的意义了。所以每个隐层都会配一个激活函数,提供非线性变化。
二、BP算法
1.BP算法基本思想
BP算法全称叫作误差反向传播(error Back Propagation,或者也叫作误差逆传播)算法。其算法基本思想为:在上述的前馈网络中,输入信号经输入层输入,通过隐层计算由输出层输出,输出值与标记值比较,若有误差,将误差反向由输出层向输入层传播,在这个过程中,利用梯度下降算法对神经元权值进行调整。
2.BP算法的推导
2.1 数学基础理论
2.2推导过程
- 正向传播求损失,反向传播回传误差
- 根据误差信号修正每层的权重
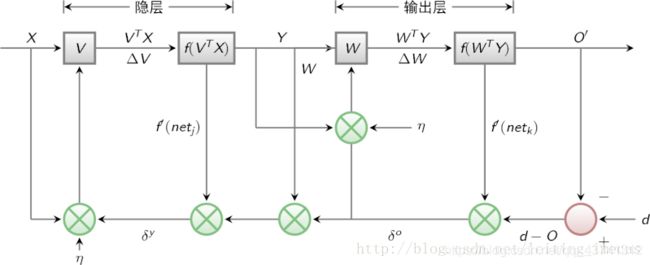
- f是激活函数;f(netj)是隐层的输出; f(netk)是输出层的输出O; d是target
结合BP网络结构,误差由输出展开至输入的过程如下:

有了误差E,通过求偏导就可以求得最优的权重。(不要忘记学习率)
3. 举例说明
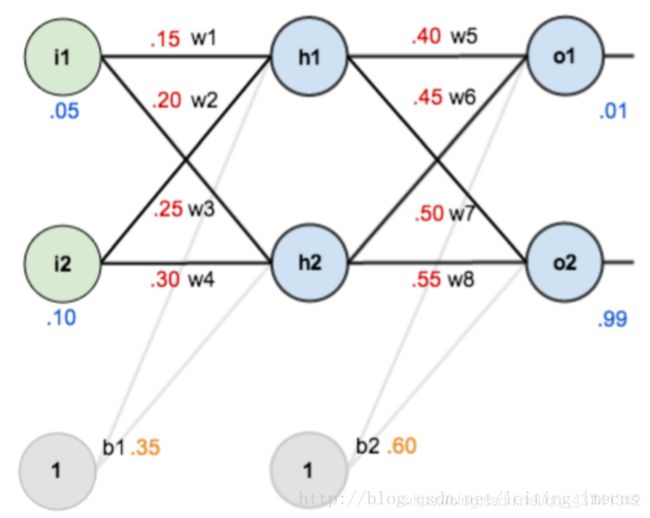
图中元素:
两个输入;
隐层: b1, w1, w2, w3, w4 (都有初始值)
输出层:b2, w5, w6, w7, w8(赋了初始值)
3.1 前向传播
3.2 反向传播

参数更新:

求误差对w1的偏导 :

注意,w1对两个输出的误差都有影响
通过以上过程可以更新所有权重,就可以再次迭代更新了,直到满足条件。
三、python代码实现
以上述例子,用python可写出如下代码,并附有详解:
import numpy as np
import matplotlib.pyplot as plt
import math
a=np.array([0.05,0.1]) #a1,a2的输入值
weight1=np.array([[0.15,0.25],[0.2,0.3]]) #a1对b1,b2的权重,a2对b1,b2的权重
weight2=np.array([[0.4,0.5],[0.45,0.55]]) #b1对c1,c2的权重,b2对c1,c2的权重
target=np.array([0.01,0.99])
d1=0.35 #输入层的偏置(1)的权重
d2=0.6 #隐藏层的偏置(1)的权重
β=0.5 #学习效率
#一:前向传播
#计算输入层到隐藏层的输入值,得矩阵netb1,netb2
netb=np.dot(a,weight1)+d1
#计算隐藏层的输出值,得到矩阵outb1,outb2
m=[]
for i in range(len(netb)):
outb=1.0 / (1.0 + math.exp(-netb[i]))
m.append(outb)
m=np.array(m)
#计算隐藏层到输出层的输入值,得矩阵netc1,netc2
netc=np.dot(m,weight2)+d2
#计算隐藏层的输出值,得到矩阵outc1,outc2
n=[]
for i in range(len(netc)):
outc=1.0 / (1.0 + math.exp(-netc[i]))
n.append(outc)
n=np.array(n)
#二:反向传播
count=0 #计数
e=0 #误差
E=[] #统计误差
#梯度下降
while True:
count+=1
#总误差对w1-w4的偏导
pd1=(-(target[0]-n[0])*n[0]*(1-n[0])*weight2[0][0]-(target[1]-n[1])*n[1]*(1-n[1])*weight2[0][1])*m[0]*(1-m[0])*a[0]
pd2=(-(target[0]-n[0])*n[0]*(1-n[0])*weight2[0][0]-(target[1]-n[1])*n[1]*(1-n[1])*weight2[0][1])*m[0]*(1-m[0])*a[1]
pd3=(-(target[0]-n[0])*n[0]*(1-n[0])*weight2[1][0]-(target[1]-n[1])*n[1]*(1-n[1])*weight2[0][1])*m[0]*(1-m[0])*a[0]
pd4=(-(target[0]-n[0])*n[0]*(1-n[0])*weight2[1][1]-(target[1]-n[1])*n[1]*(1-n[1])*weight2[0][1])*m[0]*(1-m[0])*a[1]
weight1[0][0]=weight1[0][0]-β*pd1
weight1[1][0]=weight1[1][0]-β*pd2
weight1[0][1]=weight1[0][1]-β*pd3
weight1[1][1]=weight1[1][1]-β*pd4
#总误差对w5-w8的偏导
pd5=-(target[0]-n[0])*n[0]*(1-n[0])*m[0]
pd6=-(target[0]-n[0])*n[0]*(1-n[0])*m[1]
pd7=-(target[1]-n[1])*n[1]*(1-n[1])*m[0]
pd8=-(target[1]-n[1])*n[1]*(1-n[1])*m[1]
weight2[0][0]=weight2[0][0]-β*pd5
weight2[1][0]=weight2[1][0]-β*pd6
weight2[0][1]=weight2[0][1]-β*pd7
weight2[1][1]=weight2[1][1]-β*pd8
netb=np.dot(a,weight1)+d1
m=[]
for i in range(len(netb)):
outb=1.0 / (1.0 + math.exp(-netb[i]))
m.append(outb)
m=np.array(m)
netc=np.dot(m,weight2)+d2
n=[]
for i in range(len(netc)):
outc=1.0 / (1.0 + math.exp(-netc[i]))
n.append(outc)
n=np.array(n)
#计算总误差
for j in range(len(n)):
e += (target[j]-n[j])**2/2
E.append(e)
#判断
if e<0.0000001:
break
else:
e=0
print(count)
print(e)
print(n)
plt.plot(range(len(E)),E,label='error')
plt.legend()
plt.xlabel('time')
plt.ylabel('error')
plt.show()
四、BP神经网络的优缺点
BP神经网络的优点:
- 非线性映射能力
- 泛化能力
- 容错能力,允许输入样本中带有较大误差甚至个别错误。反应正确规律的知识来自全体样本,个别样本中的误差不能左右对权矩阵的调整
BP神经网络的缺陷:
- 需要的参数过多,而且参数的选择没有有效的方法。确定一个BP神经网络需要知道:网络的层数、每一层神经元的个数和权值。权值可以通过学习得到,如果,隐层神经元数量太多会引起过学习,如果隐层神经元个数太少会引起欠学习。此外学习率的选择也是需要考虑。目前来说,对于参数的确定缺少一个简单有效的方法,所以导致算法很不稳定;
- 属于监督学习,对于样本有较大依赖性,网络学习的逼近和推广能力与样本有很大关系,如果样本集合代表性差,样本矛盾多,存在冗余样本,网络就很难达到预期的性能;
- 由于权值是随机给定的,所以BP神经网络具有不可重现性;