Pytorch中的序列化容器-度消失和梯度爆炸-nn.Sequential-nn.BatchNorm1d-nn.Dropout

Pytorch中的序列化容器-度消失和梯度爆炸-nn.Sequential-nn.BatchNorm1d-nn.Dropout

1. 梯度消失和梯度爆炸

在使用pytorch中的序列化 容器之前，我们先来了解一下常见的梯度消失和梯度爆炸的问题

1.1 梯度消失    【梯度太小，无法进行参数的更新，梯度小到数据类型无法表示时出现NAN】

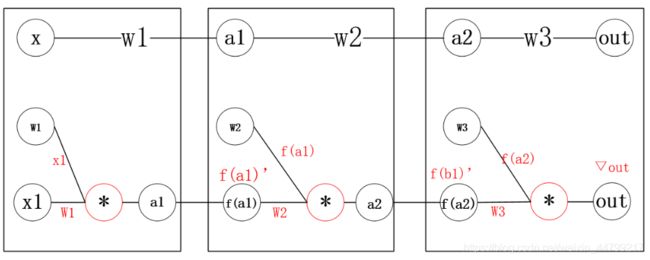
假设我们有四层极简神经网络：每层只有一个神经元

获取w1的梯度有：▽w1 = x1f(a1)’w2f(b1)’w3*▽out

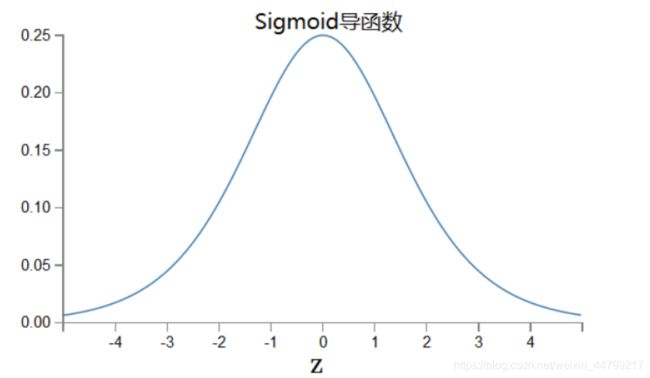
假设我们使用sigmoid激活函数，即f为sigmoid函数，sigmoid的导数如下图

假设每层都取得sigmoid导函数的最大值1/4，那么在反向传播时，X1=0.5,w1=w2=w3=0.5​

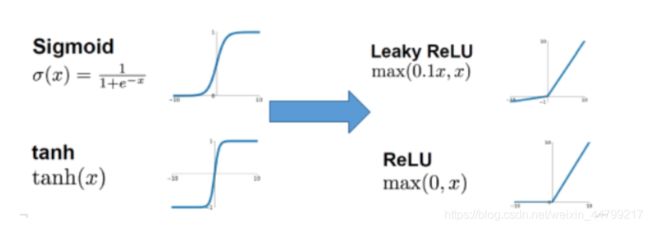
当权重初始过小或使用易饱和神经元(sigmoid,tanh，) sigmoid在y=0,1处梯度接近0，而无法更新参数，时神经网络在反向传播时也会呈现指数倍缩小，产生“消失”现象。

 

1.2 梯度爆炸    【梯度太大，大到数据类型无法表示，出现NAN】

假设X2=2,w1=w2=w3=2​

当权重初始过大时，梯度神经网络在反向传播时也会呈现指数倍放大，产生“爆炸”现象。

1.3 解决梯度消失或者梯度爆炸的经验   【1.使用更加容易计算梯度的激活函数 2.使用改进的优化算法 3.使用batch Normalization】

1. 替换易训练神经元

1. 改进梯度优化算法：使用adam等算法

2. 使用batch normalization

 

2. nn.Sequential

nn.Sequential是一个有序的容器，其中传入的是构造器类(各种用来处理input的类)，最终input会被Sequential中的构造器类依次执行

例如：

layer = nn.Sequential(
            nn.Linear(input_dim, n_hidden_1), 
            nn.ReLU(True)， #inplace=False 是否对输入进行就地修改，默认为False
            nn.Linear(n_hidden_1, n_hidden_2)，
            nn.ReLU(True)，
            nn.Linear(n_hidden_2, output_dim) # 最后一层不需要添加激活函数
             )

在上述过程中，可以直接调用layer(x)，得到输出

x的被执行顺序就是Sequential中定义的顺序：

1. 被隐层1执行，形状变为[batch_size,n_hidden_1]

2. 被relu执行，形状不变

3. 被隐层2执行，形状变为[batch_size,n_hidden_2]

4. 被relu执行，形状不变

5. 被最后一层执行，形状变为[batch_size,output_dim]

 

3. nn.BatchNorm1d  【加速模型的训练，把参数进行规范化的处理，让参数计算的梯度不会太小】

batch normalization 翻译成中文就是批规范化，即在每个batch训练的过程中，对参数进行归一化的处理，从而达到加快训练速度的效果。

以sigmoid激活函数为例，他在反向传播的过程中，在值为0,1的时候，梯度接近0，导致参数被更新的幅度很小，训练速度慢。但是如果对数据进行归一化之后，就会尽可能的把数据拉倒[0-1]的范围，从而让参数更新的幅度变大，提高训练的速度。

batchNorm一般会放到激活函数之后，即对输入进行激活处理之后再进入batchNorm

layer = nn.Sequential(
            nn.Linear(input_dim, n_hidden_1),
    		
            nn.ReLU(True)， 
    		nn.BatchNorm1d(n_hidden_1)
    
            nn.Linear(n_hidden_1, n_hidden_2)，
            nn.ReLU(True)，
    		nn.BatchNorm1d(n_hidden_2)

            nn.Linear(n_hidden_2, output_dim) 
             )

4. nn.Dropout

dropout在前面已经介绍过，可以理解为对参数的随机失活

1. 增加模型的稳健性

2. 可以解决过拟合的问题（增加模型的泛化能力）

3. 可以理解为训练后的模型是多个模型的组合之后的结果，类似随机森林。

layer = nn.Sequential(
            nn.Linear(input_dim, n_hidden_1),
            nn.ReLU(True)， 
    		nn.BatchNorm1d(n_hidden_1)
    		nn.Dropout(0.3) #0.3 为dropout的比例，默认值为0.5
    
            nn.Linear(n_hidden_1, n_hidden_2)，
            nn.ReLU(True)，
    		nn.BatchNorm1d(n_hidden_2)
    		nn.Dropout(0.3)
    
            nn.Linear(n_hidden_2, output_dim) 
             )