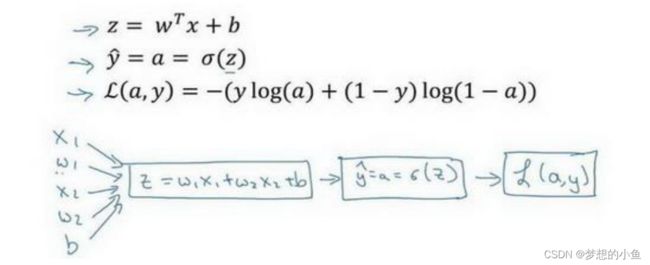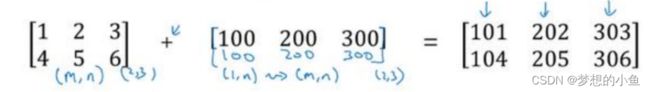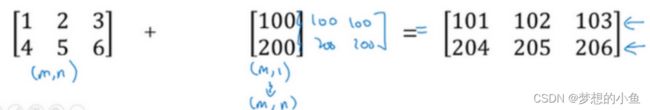吴恩达《机器学习》学习笔记（一）
目录
一、机器学习
什么是神经网络？
为什么要引入ReLU？
监督学习 supervised learning
为什么深度学习会兴起？
二、Logistic regression
二分类
逻辑回归模型
代价函数 cost function
为什么需要代价函数？
损失函数loss function
梯度下降gradient decent
计算图
向量化
numpy 广播机制
一、机器学习
什么是神经网络？
神经网络类似一个函数y=f(x)，神经网络可以训练出一个非常精准的函数。我们可以借此来完成相关的下游任务。
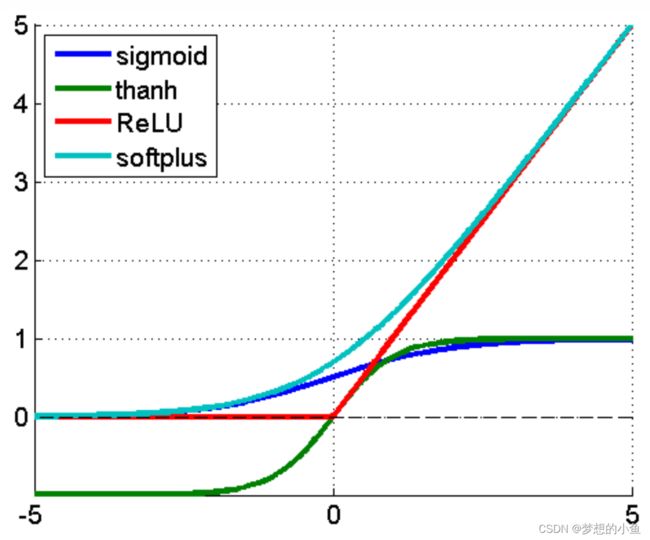
ReLU激活函数，它的全称是Rectified Linear Unit
为什么要引入ReLU？
1、采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
2、对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
3、ReLu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。
监督学习 supervised learning
监督学习是机器学习的一周类别，目前使用最多的是在线广告。
RNN（recurrent neural network）:时间序列数据处理
CNN（Convolutional neural network）:图像处理
Training时设计到的数据分为structured和unstructured（图像、语音、文本）
为什么深度学习会兴起？
数字化社会提供了大量数据信息；在大数据的环境下，深度学习取得的效果比传统机器学习要好；机器设备更加先进；算法不断更新。
二、Logistic regression
二分类
逻辑回归是一个用于二分类的算法。
训练部分包括前向和反向传播
对于图片数据，可以提取三通道的像素值来获取特征向量
一张图片，需要保存三个矩阵，分别对应图片中的红、绿、蓝三种颜色通道，代表对应图片中红、绿、蓝三种像素的强度值。
在python中可以使用 X.shape 来获取数据集矩阵的大小(, ) Y.shape 获取对应标签(1, )
逻辑回归模型
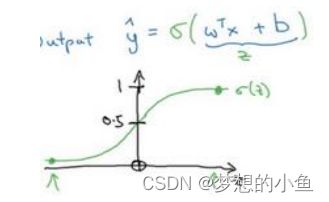
怎么使用逻辑回归去处理一个图像问题？例如这张图片是不是一只猫? 使用一个简单的函式
去获取你这是一只猫的图片的机率，利用sigmoid函数
将值域映射到[0,1]。
同时我们注意到，当x的取值在两端时，函数的斜率趋近于0，这里会造成梯度消失的现象。
代价函数 cost function
为什么需要代价函数？
因为需要通过代价函数来更新我们的参数，代价函数可以看成一个目标函数，放映当前模型的好坏程度。
损失函数loss function
一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我们在逻辑回归模型中会定义相关熵损失函数
Ly,y=-ylog(y)-(1-y)log(1-y)
如果等于1，我们就尽可能让y
变大，如果y等于0，我们就尽可能让y
变小
损失函数只适用于单个训练样本，而代价函数是参数的总代价，对于每一个样本的损失函数求和取平均。
梯度下降gradient decent
实际情况的函数可能是非凸且有多个local minima ，故我们可以假设代价函数为凸函数初始化参数，也可以随机初始化。对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。
参数更新：w=w-lrdJ(w)dw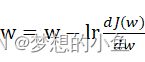
，lr表示学习率，用来控制步长。
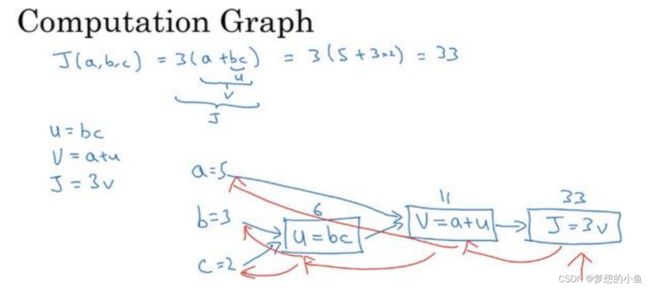
计算图
正向
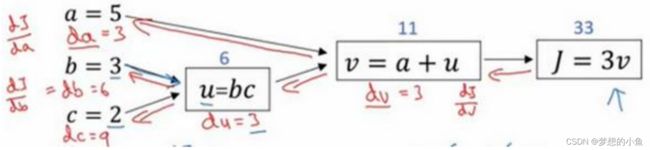
反向（链式法则）
对于logistic regression而言，
最后结果：dL(a,y)dz=a-y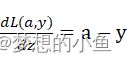
w=w-lrdzdw1n(a-y)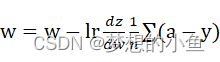
对于n个样本，即取平均进行更新
缺点：第一个for循环是一个小循环遍历个训练样本，第二个for循环是一个遍历所有特征的 for循环。
向量化
z=0
for i in range(n_x)
z+=w[i]*x[i]
z+=b可以使用z=np.dot(w,x)+b代替
示例代码
import numpy as np #导入 numpy 库
a = np.array([1,2,3,4]) #创建一个数据 a
print(a)
# [1 2 3 4]
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过 round 随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(“Vectorized version:” + str(1000*(toc-tic)) +”ms”) #打印一下向量化的版本的时间
#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
c += a[i]*b[i]
toc = time.time()
print(c)
print(“For loop:” + str(1000*(toc-tic)) + “ms”)#打印 for 循环的版本的时间numpy 库有很多向量函数。比如 u=np.log 是计算对数函数()、np.abs()是计算数据的绝对值、np.maximum() 计算元素 中的最大值，你也可以np.maximum(v,0) 、∗∗2代表获得元素每个值得平方、1/获取元素 的倒数等等。所以当你想写循环时候，检查numpy是否存在类似的内置函数，从而避免使用循环(loop)方式。
利用个训练样本一次性计算出小写和小写a
Z = np.dot(w.T,X) + b
Broadcast: 实数 扩展成一个 1 × 的行向量
A.sum(axis=0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行，在numpy中，0轴是垂直的，也就是列，而1轴是水平的，也就是行。
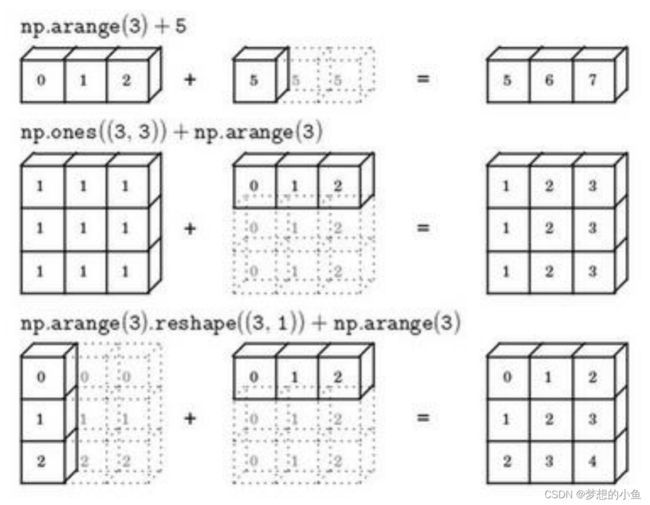
numpy 广播机制
矩阵（3,4）后缘维度的轴长度是4，而矩阵 （1,4）的后缘维度也是4，则他们满足后缘维度轴长度相符，可以进行广播。广播会在轴长度为1的维度进行，轴长度为1的维度对应axis=0，即垂直方向，矩阵cal（1,4）沿axis=0(垂直方向)复制成为cal_temp（3,4），之后两者进行逐元素除法运算。
