吴恩达老师的机器学习与深度学习贴

吴恩达老师的机器学习与深度学习贴

机器学习第一周：
首先，老师举例说明，机器学习的几个显示生活中的例子：包括无人机的实验运行，垃圾邮件的识别，软件APP的内容推广，甚至谷歌新闻的同一类型的内容分块等等。
机器学习主要是包括三大类：无监督式学习，有监督式学习，以及加强式学习。老师主要涉及的内容是前两项，有监督和无监督学习。
无监督学习：给计算机一堆数据，让计算机自行处理，主要是进行聚类处理。
有监督学习：给计算机两类数据集，包括训练集和测试集，验证集则是给了计算机正确的答案，进而去训练模型，验证集验证模型效果。

ps:本课程有课后作业，主要基于matlab。作业及相关代码下载地址：

https://github.com/TingNie/Coursera-ML-using-matlab-python

机器学习第二周
第二周主要是关于回归预测的一周。

  首先，老师给了一些房子面积和房价的数据，来预测下没有给出的房子面积相应的房价-------回归分析。

  然后，回归分析经常用到的一些符号:
m:提供的样本数；
y:输出；
（x⁽ⁱ⁾,y⁽ⁱ⁾）:第i个样本
h：回归预测的假设函数（来自单词hypothesis）

  接着，线性回归的例子：
假设函数：h_θ（x）=θ₀+θ₁x
若需要此假设函数能够比较好的拟合样本，则还要引入一个代价函数：

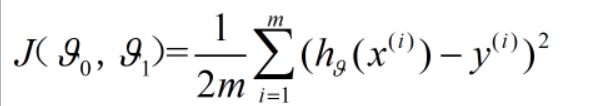
  回归预测的目标就是，改变θ₀和θ₁让代价函数最小，此时预测出来了相应的假设函数，最拟合样本点。

  之后，介绍了梯度下降的概念及数学思想：
梯度下降步骤：1，给函数里面的变量设初值，2，使变量向着函数输出值最小的方向移动，最终找到是函数值最小的变量值。
所以代价函数也是为了找到使函数值最小的变量，此时刚好契合了梯度下降的思想，以下公式代入代价函数。
梯度下降公式：

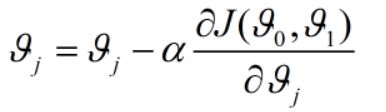
α：学习速率，控制参数变化的快慢。
对于j=0：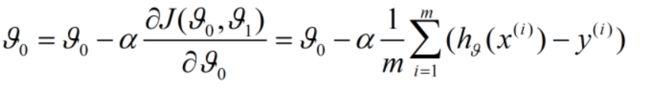
对于j=1：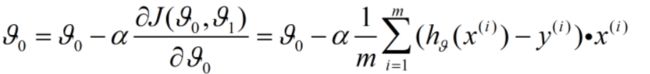

数学思想：

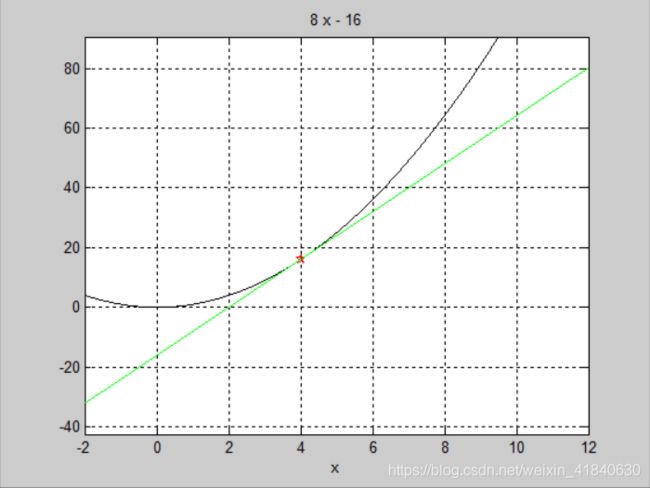
  为了更好的理解梯度下降的思想，假设此时梯度下降的目标函数y=f(x)为只含有一个变量的函数，设定初值为红点所在的位置，通过图中我们可以看到函数的最小值在初值的左边，即初值应该变小才对。
  绿线是初始值的切线，切线上升即导数为正，原先的x值减去导数（正数），是往左移动的，简单证明了梯度下降的数学思想。

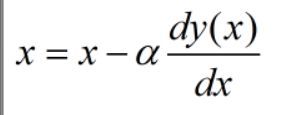
  关于梯度下降的几点说明：
  1.有可能梯度下降找到的是局部或者全局最优解，但对于线性回归来说，局部最优和全局最优是一个值；
  2.在接近最优解的时候，导数（或者偏导）已经变得很小，因为最优解处的导数（或者偏导）为0，所以α不用在此处设置很小值；
  3，对于用到全部样本的梯度下降，有个术语称之为：Batch梯度下降。

作业题：线性回归
得到的知识点：(x和y都是m行1列的向量)
1.对于h函数(h=theta0+theta1x)计算可以利用矩阵相乘：
theta=[theta0;theta1];X=[ones(m,1),x];h=Xtheta；
2.计算导数：differ_theta1=sum(（X✳theta-y）.✳X(:,2))/(2m);
3.行向量乘列向量等于平方和

机器学习第三周
  讲述了矩阵的加减乘除以及一些特性：
如：有多组theta值theta=[theta0，theta0s，theta0ss；
        theta1，theta1s，theta1ss];
X（同上定义），X✳theta表示第一列为第一组theta值预测的输出，同理第二列为第二组预测的输出，第三列是第三组预测的输出。

机器学习第四周
  讲述了有多个特征的样本的线性预测：
一.符号表示
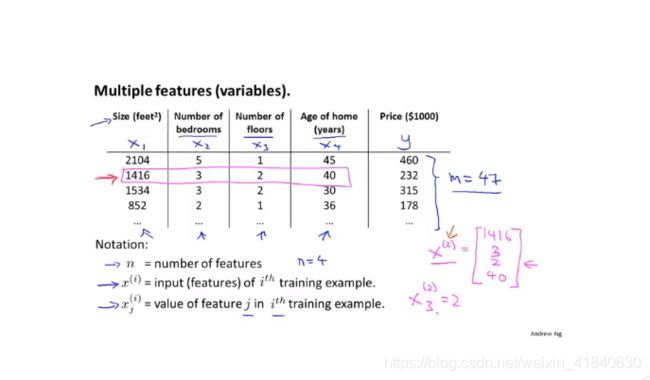
m:样本个数，如在图中样本数为4；
n:特征个数，如在图中每个样本的特征个数为4；
x⁽ⁱ⁾:第i个样本的所有特征，如在图中x⁽²⁾=[1416,3,2,40];
x⁽ⁱ⁾_j:第i个样本的所有特征里的第j个，如在图中x⁽²⁾₃=2；

二.假设函数（利用矩阵相乘）
  对于h函数(h=theta0+theta1x1+theta2x2+theta3x3…),其中x1,x2,x3…是某一个样本的n个特征。
  计算可以利用矩阵相乘：
theta=[theta0;theta1,theta2,theta3,…];(theta为n+1)
X=[ones(m,1),x];
(x为mXn矩阵，m个样本，n个特征，X为mXn+1)
h=X*theta；
三.代价函数

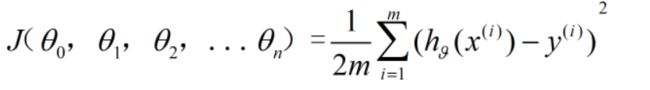
四.梯度下降

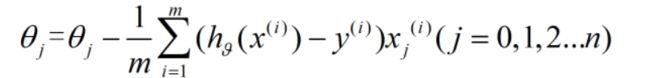
注意：对于j=0,x⁽ⁱ⁾_j=1;

五.特征缩放
目的：加快收敛速度，减少迭代次数；
特点：让特征在[-1，1]范围附近，如[-3,2]是允许的，但是[-100，100]就不太好；
方法1：让所有特征向量除以本类特征的最大值；
方法2：让所有特征向量减去本类特征的平均值，再除以本类特征的范围，即本类特征的最大值减最小值

六.多项式回归
有两个知识点：
1，如下图特征就一个x,但是有它的平方和立方，这时候可以看作有三个特征，x,x²,x³

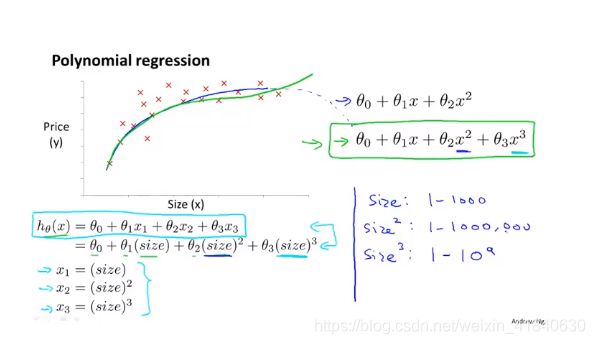
2,用二次多项式回归反而会随着横坐标的增长而下降，有时候是不符合现实情况的，可以采用平方根的形式。

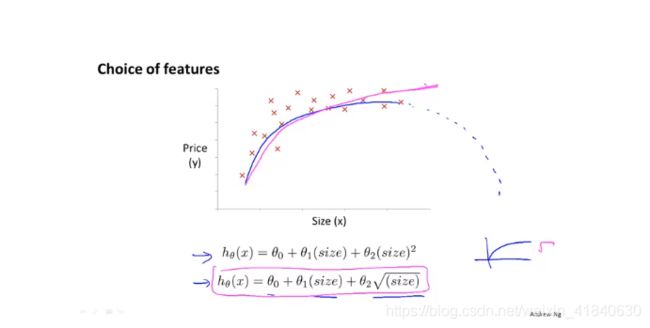
七，正规方程
  正规方程是一种快速解决theta最优值的方法：

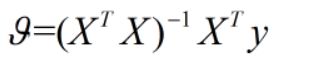
这里仍然是大写的x,来源同上，y是列向量（m x 1）,
X( m x n+1)
注意点：
1，对于求逆，在程序里用的是pinv函数，求的是伪逆；
2，一般不存在没有逆矩阵的请况，如果存在检查下特征里面是不是存在有线性关系的两个特征，还有可能是特征数大于样本数。
3，关于正规方程方法和梯度函数方法求theta，一般特征数小于10⁴
选择正规方程，特征数大于10⁴，选择梯度函数。

机器学习第五周
  主要讲述了octave软件的编程，有点像Linux和matlab的结合。
如pwd:当前路径，
cd：改变路径
ls：现在路径下的文件
其他的话，矩阵运算，变量运算像matlab
技巧：
A（：）：把所有的数据按列排成一列