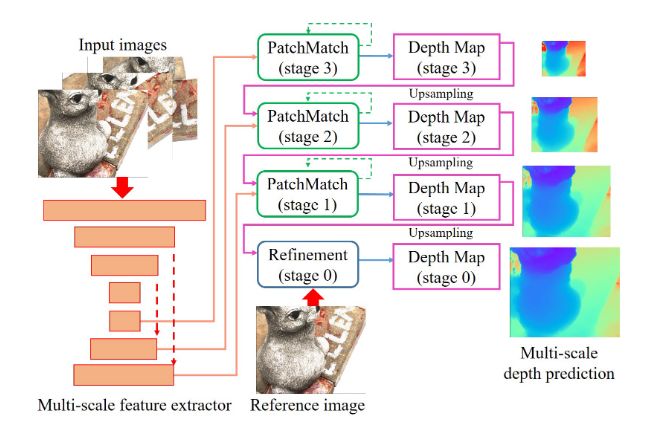
PatchmatchNet理解与学习

PatchmatchNet: Learned Multi-View Patchmatch Stereo

摘要

现有的基于深度学习的MVS网络，多为基于3D代价体，此方法根据Plane sweeping算法，首先在参考相机视锥空间划分相应的深度假设平面，因此面要想实现精细的重建效果，则深度假设平面也需相应的增加，由此导致内存消耗和运行时间增加，难以运用于高分辨率场景。
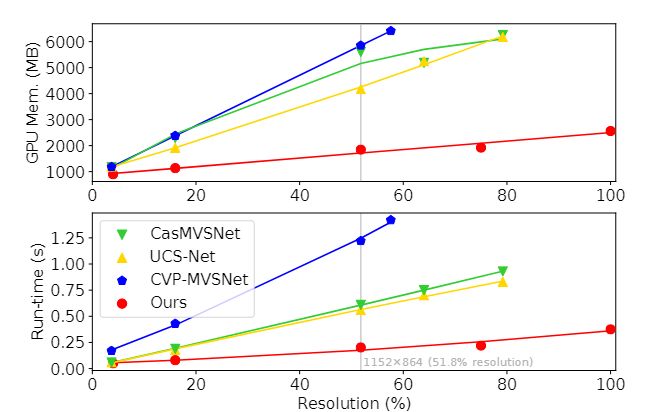
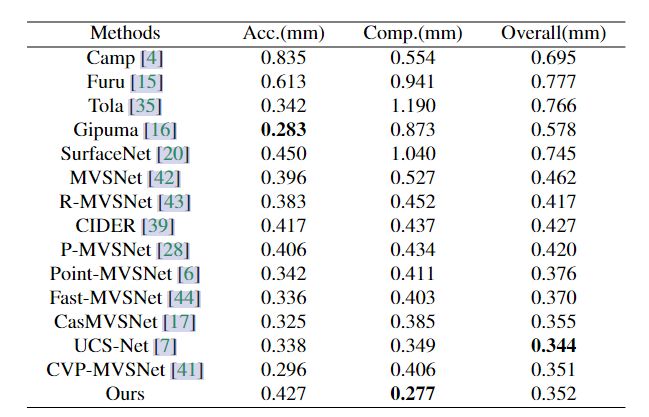
本文首次将patchmatch算法用于基于深度学习的多视图立体领域，与基于3D代价体正则化的方式相比，文中提出的方法显存消耗更小，运行时间更短。

网络

Patchmatch基本的流程可分为：

1. 特征提取
2. 基于学习的Patchmatch迭代
3. 深度图细化

1.特征提取

文中的网络结构为级联的网络结构，所以采用了特征金字塔网络来进行多尺度的特征提取

2.基于深度学习Patchmatch

和传统的Patchmatch的算法类似，本文提出的基于深度学习的Patchmatch基本流程如下：

1. 初始化：生成随机假设
2. 传播：向领域帧传播
3. 评估：计算相应patch的匹配代价，选择最佳的一个

2.1初始化和局部扰动

初始化：首次深度假设，也就是在stage 3阶段，由于没有深度图，文中通过对$[d_{min},d_{max}]$的逆深度范围对每个像素深度假设值$D_f$进行随机采样，为了确保均匀的覆盖深度范围，将你深度范围划分了$D_f$个区间，确保了每个每个区间都有一个深度值。

局部扰动：对于后续的stage K阶段，给定一个逆深度范围$R_k$，在这个范围内对每个像素点P均匀的生成$N_k$个假设点，也就是说在$R_k$的范围内，给像素点P在假设的深度层上层或者下层取样几个点，这几个点的是与P深度不一致的假设点。随着越来越精细的迭代进行，每个阶段的$R_k$不断减小，$R_k$的中心由上一阶段的结果所定义。这样给每个像素点都给出了一个局部扰动。

2.2自适应传播

设计理念：每个物体表面的上每个像素深度值之间的相关性，只与某个像素所在的同一物理表面上的像素有关。例如下图中的黄点，他的深度值只与猫表面其余点的深度值有关，而与桌子上的点无关，所以在传播过程中，自适应的在同一物理表面上的像素点进行传播。

基于可变形卷积神经网络而设计的。
为了学习参考图像中像素点P的深度假设$K_p$，在参考图像特征图$F_0$上运用2D CNN学习每个像素点的2D偏移量${\{\Delta O_i(p)\}}_{i=1}^{K_p}$，这些偏移量是在固定的2D偏移${\{O_i\}}_{i=1}^{K_p}$上发生的（可以这样理解，所谓的固定的2D偏移量就是相当于取参考图像的每个像素点P的邻域内的点，这个取样范围就是${\{O_i\}}_{i=1}^{K_p}$，由于这个固定的取样范围可能导致在取的邻域点和像素点P不在同一个物理平面内，所以在这些取样的邻域点上施加一个2D偏移量，并且通过2DCNN卷积操作，保证了每个邻域点偏移后都与像素点p在同一个物理平面中），形成了网格的结构，并通过双线性插值获得深度假设$D_p(P)$:$D_p(p)={\{D(p+O_i+\Delta o_i(p))\}}_{i=1}^{K_p}$，其中D是上一阶段迭代的深度图。

2.3自适应评估

自适应评估一共分为：可微变换（differentiable warping），匹配代价计算，自适应代价聚合，深度回归。

differentiable warping：给定参考相机和源相机的相机参数，计算参考图像中像素点$P_i(d_j)$在源图像中对应像素点$P_{i,j}$。

${\{K_i\}}_{i=0}^K$为内参举证
${\{[R_{0,i}|t_{0,i}]\}}_{i=1}^K$为参考相机和源相机之间的变换
$d_j$为参考图像下P的深度

通过可微双线性插值来获得视图 i 和第 j 组单应性变换后的源图像特征图$F_i(p_{i,j})$的深度假设。

匹配代价计算：对于基于深度学习的MVS网络，计算匹配代价是将任意数量的源图像中每个像素点p的深度假设值$d_j$聚合到一个视差空间中。
本文使用group-wise来计算代价，通过像素视图权重来对每个视图进行聚合。随后通过小型的网络，将每个group代价投影到一个数字。

参考图像的特征图$F_0(P)$和源图像的特征图$F_i(p_{i,j})$的特征通道channel分成G组，每组的特征图为{${F_0(P)}^g$，${F_i(p_{i,j})}^g$}$\in {\mathbb{R}}^C$计算他们第g组的相似度${S_i(p,j)}^g\in {\mathbb{R}}^{W\times H\times D\times G}$

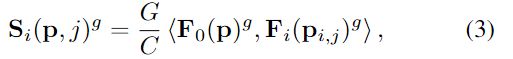
其中$<.,.>$表示内积，$S_i$的维度为H×W×D×G。

参考图像上的像素点p对应到每个源图像的权重${\{w_i(p)\}}_{i=1}^{N-1}$，简单来说就是每张源图像上与像素点P对应的点p’为p点的贡献度是多少。用$w_i(p)$表示源图像$I_i$中p’的可见信息（应该是颜色、光照之类的）。得到的逐像素的权重图只计算一次，之后的每个stage k都是将这张权重图进行上采样用于更为精细的迭代。
这个简单的逐像素权重网络由卷积核为1×1×1的3D卷积层和非线性的Sigmoid函数组成，网络的输入为初始的相似度$S_i$，每个像素的输出为0-1之间的值，这个输出是对每个深度假设层的，所以$P_i\in {\mathbb{R}}^{W\times H\times D}$。因此，像素点p在每个源图像的对应点p‘都存在一个权重值，文中只取了最大的一个，像素 p 和源图像 $I_i$的视图权重公式为：

其中$P_i(p,j)$表示为像素点p在第j个深度假设所覆盖范围的置信度。
最终的的相似度计算为：

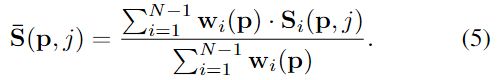
每个深度假设层都由一个$\overline{S}(p,j)$，而且只是一个group上的所以最终$\overline{S}(p,j)\in {\mathbb{R}}^{W\ast H\ast D\ast G}$，为了将其构建为一个整体的代价空间C，采用了一个卷积核大小为1×1×1的3D卷积层进行降维。

自适应空间代价聚合
虽然在多尺度特征提取时已经聚合了部分特征，本文还是采用和传统的MVS类似代价聚合方式，空间代价聚合。提出了基于Patchmatch stereo和AANet的自适应空间代价聚合方法。对于空间窗口$K_e$，像素${\{p_i\}}_{k=1}^{K_e}$呈网格分布，我们学习每个像素的附加2D偏移量${\{\Delta p_i\}}_{k=1}^{K_e}$，聚合的空间代价为：

和自适应传播类似，其中${\{{\omega }_k\}}_{k=1}^{K_e}$为空间特征相似性权重，${\{d_k\}}_{k=1}^{K_e}$为深度假设相似性权重。在给定的采样位置${\{p+p_k+\Delta p_k\}}_{k=1}^{K_e}$采用双线性插值从$F_0$中提取特征。采样位置的特征和p之间通过group-wise correction。将每个group的结构链接为一个整体，通过一个卷积核大小为1 × 1 × 1的3D卷积和非线性的sigmoid函数，输出描述每个采样点和 p 之间相似性的归一化权重。

深度回归：通过softmax将代价体装变为概率体P，得到子像素的回归深度值以及置信度。p处的回归深度值为

2.4深度图细化

基于MSG-Net设计了一个深度残差网络，为了避免对某个深度产生偏差，将深度图的深度值缩放到[0,1]范围内，在细化后转变回来。该网络的输出为残差值，将该残差值加到Patchmatch的深度估计上采样D中，获得细化后的深度图$D_{ref}$。这个网络独立的从D和$I_0$提取特征图$F_D,F_0$,对F_D进行上反卷积以达到上采样至原图像大小的目的。为了取得深度残差值，在这两个特征图的链接处运用了多个2D卷积层。

2.4损失函数

损失函数$L_{total}$将所有深度估计和以相同分辨率渲染的地面真实之间的损失进行加和，得到最终的损失函数表达式如下：

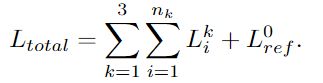
对于每一个阶段的Patchmatch的i次迭代损失$L_i^k$采用的$L_1$损失函数，而$L_{ref}^0$则是最后的那个被refine过的深度层的$L_1$损失。

3.结果（只看DTU数据集）

显存消耗

排名

4.消融实验