Reinforcement Learning Enhanced Heterogeneous Graph Neural Network阅读笔记

强化学习增强异质图神经网络

代码源：https://github.com/zhiqiangzhongddu/RL-HGNN

摘要

异构信息网络(HINs)涉及多种节点类型和关系类型，在许多实际应用中非常普遍。近年来，异质图表示学习(heterogeneous graph representation learning, HGRL)得到了越来越多的关注，其目的是将HIN中丰富的结构和语义信息嵌入到低维节点表示中。到目前为止，大多数HGRL模型依赖于手工定制元路径来捕获给定HIN的底层语义。然而，依赖于手工制作的元路径需要丰富的领域知识，而对于复杂和语义丰富的HINs来说，获取这些知识是极其困难的。此外，严格定义的元路径将限制HGRL对HINs中更全面的信息的访问。为了充分释放HGRL的力量，我们提出了强化学习增强的异构图形神经网络(RL-HGNN)，为HIN中的节点设计不同的元路径。具体来说，RL-HGNN将元路径设计过程建模为马尔可夫决策过程，并使用策略网络自适应地为每个节点设计元路径，以学习其有效表示。利用模型在下游任务上的性能，利用深度强化学习对策略网络进行训练。我们进一步提出了一个扩展，RL-HGNN++，以改进元路径设计过程，加快训练过程。实验结果证明了RL-HGNN的有效性，并揭示了它可以识别可能被人类知识忽略的有意义的元路径。

介绍

现实世界数据中的复杂交互，如社会网络、生物网络和知识图，可以被建模为异构信息网络(HINs)[29]，它通常与多种类型的对象(节点)和元关系相关联。以图1-(a)所示的异构学术网络为例，涉及论文、作者、机构、出版场所等四种类型的节点，以及这些节点之间的八种元关系。由于HINs能够保留节点之间丰富而复杂的相互依赖关系，因此越来越受到研究界的关注，最近被应用于推荐系统[17,39]、信息检索[26,36]等领域。然而，HINs的复杂语义和非欧几里得性质使得传统机器学习模型难以建模。

在过去的十年中，HIN 的一个重要研究方向是异构图表示学习（HGRL）。 HGRL 的目标是学习节点潜在表示，这些表示对图结构、多类型节点和元关系进行编码，用于下游任务，包括链接预测 [37]、节点分类 [16,38] 和节点聚类 [10]。 正如最近的一项调查 [7] 中所讨论的，HGRL 的传统范式之一是手动定义和使用元路径来对 HIN 的结构进行建模，并利用随机游走将图结构转换为序列 [6,9]，可以对其进行探索 通过基于浅层序列的嵌入学习算法，例如 DeepWalk [23] 和 node2vec [12]。 HIN 的元路径方案被定义为 HIN 网络模式上的元关系序列。例如，图1-(a)中的异质学术网络中的一个说明性元路径是$Author\stackrel{\text{ Cite }}{⟶}Author\stackrel{\text{ Write }}{⟶}Paper$.“浅层”方法被描述为一个嵌入查找表，这意味着它们直接将每个节点编码为一个向量，而这个嵌入表是要优化的参数。

图1：一个HIN的玩具例子和一些可能的方法:(A)一个学术HIN;(b)从(a)导出的一些示例元路径。

最近，鉴于图神经网络 (GNN) [13,19,34,41] 的巨大成功，HGRL 的第二范式尝试为 HGRL [10,16,25,38] 设计异构图神经网络 (HGNN) ,42]，它使用预定义的元路径扩展了 HIN 上的图卷积操作。 与 HGRL 的“浅层”方法相比，HGNNs 支持端到端的训练机制，可以在一些标记节点的指导下学习节点表示。它们还通过更复杂的编码器进行授权，而不是使用浅层嵌入学习算法。编码器通常采用深度神经网络的形式，能够对 HIN 中的结构和节点属性进行自然建模。

HGRL的关键挑战. 然而，HINs上的节点表示学习任务仍然不是简单的，这主要是因为它依赖于手工制作的元路径。例如，元路径的设计需要丰富的领域知识，而在复杂且语义丰富的HINs[7]中，这是极难获得的。具体而言，给定一个节点类型集为$\mathcal{N}$的HIN $G$，关系类型集$\mathcal{R}$和固定的元路径长度$T$.可能的元路径包含在一组大小$(|\mathcal{N}|\times |\mathcal{R}|)$中。当增加$|\mathcal{N}|$，$|\mathcal{R}|$和$T$的规模时，这种巨大的集合会导致组合爆炸。其次，手动设计的元路径的表示能力仅限于特定数据上的特定任务，因为具有相同节点类型集$\mathcal{N}$和关系类型集$\mathcal{R}$的不同$G$可能具有不同的节点属性和元关系分布。它需要为每个数据集上的每个任务设计合适的元路径，这对于实际应用来说非常困难。 此外，现有的元路径引导方法简单地假设相同类型的不同节点/关系共享相同的元路径，而忽略了各个节点之间的差异。 以异构学术网络为例（图1-（a）），假设我们计划学习节点表示来确定$Authors$的研究领域。一条元路径${\Omega }_1:Author\stackrel{\text{ Write }}{⟶}Paper\stackrel{\text{ Published }}{⟶}Venue$可能对了解高级研究员的形象很有用，因为他/她发表的论文和参加的地点可能提供足够的信息来决定他/她的研究领域。当我们仅通过几篇发表的论文来了解一个初级博士候选人的表现时，我们可能需要从他的合作者中提取信息，这些合作者遵循元路径:${\Omega }_2:Author\stackrel{\text{ Cite }}{⟶}Author\stackrel{\text{ Write }}{⟶}Paper$，因为之前的元路径${\Omega }_1$在博士候选人的情况下保留的信息很少。因此，我们认为应该根据每个节点自身的属性和结构属性为其设计适当的元路径，而不是为每个节点类型提供几个通常预定义的元路径。开发一种自适应策略来为HIN中的节点设计合适的元路径是至关重要的，这在HGRL领域仍然是一个挑战。

鉴于这些确定的局限性和挑战，我们建议研究HGRL，目标是(i)学习为HINs中的每个节点自动创建合适的元路径，(ii)使用自动设计的元路径高效地生成节点表示，以及(iii)保留端到端训练策略。为了实现这些目标，我们提出了强化学习增强异质图神经网络(RL-HGNN)框架，以充分释放HGRL的力量。

RL-HGNN的关键思想. 通常，我们的目标是通过强化学习 (RL) 智能体取代人类在元路径设计上的努力，以解决对 HGNN 手工制作的元路径的依赖性的局限性。 与具有领域知识的专家相比，RL 智能体（agent，本文中采用此种翻译，下同）可以通过顺序探索和开发，根据特定任务为每个节点自适应地设计适当的元路径。 在设计元路径时同时考虑了网络结构和节点属性，这对于具有复杂语义的 HIN 具有吸引力和实用性。

如图2所示，元路径设计过程可以自然地视为马尔科夫决策过程(MDP)，在这个过程中，扩展元路径的下一个关系取决于元路径的当前状态。然后，我们提出了一个HGNN模型，对设计的元路径进行信息聚合，以学习节点表示，可以应用到下游任务，如节点分类。由于最近RL的成功[22,22]，我们建议使用一个策略网络(agent)来解决这个MDP，并使用一个由奖励函数增强的RL算法来训练策略网络。奖励函数定义为对下游任务的性能改进，鼓励RL智能体实现更好、稳定的性能。此外，我们发现在元路径上的经典信息聚合过程中存在大量的计算冗余，因此我们引入了一种最优聚合策略来实现HINs上的无冗余信息聚合。

图2：RL-HGNN 将节点 A-1 的元路径设计为马尔可夫决策过程 (MDP)。 状态 1 是节点 A-1 的属性，RL 智能体采取行动选择关系引用来扩展元路径。 然后，状态 1 更新为状态 2，即节点 A-1 和 A-2 的属性的平均值。 RL 代理进一步对状态 2 采取行动以扩展元路径。 图中还显示了根据状态 2 和动作 2 生成的元路径实例。

我们展示了我们框架的一个实例，即 RL-HGNN，通过使用经典 RL 算法（即深度 Q 学习（DQN）[22]）及其扩展 RL-HGNN++ 实现它。 RL-HGNN 根据节点的属性为每个节点找到一个元路径，而 RLHGNN++ 进一步使元路径设计能够探索 HIN 的结构语义，并考虑编码器的状态。 它还基于理论复杂性分析显着加速了 HGRL 过程。

为了验证该框架的有效性，我们在两个HINs上进行了大量的实验，实验结果表明，我们的框架优于目前最先进的模型。

主要贡献. 我们在本文中总结了我们的贡献如下:

(1) 我们提出了一个 RL 增强框架 $\text{RL-HGNN}$，可以从 HIN 中学习节点表示，而无需手动元路径设计。
(2)我们设计了一种无冗余的异构信息聚合方法，以减少元路径信息聚合过程中的冗余计算。
(3) 我们开发了我们框架的两个实际实例，RLHGNN 和 RL-HGNN++，它们改进了元路径设计程序并加速了训练过程。
(4)我们使用不同的实验设置进行节点分类任务来评估我们模型的性能。 实验结果显示了我们框架的两个实例的有效性，它们都可以识别被人类专家忽略的有意义的元路径。

2 准备工作

2.1 问题描述

定义1.(异构信息网络) 异构信息网络(HIN)是一种具有多类型节点和边的信息网络，用图表示$G=(\mathcal{V},\mathcal{E},\mathcal{N},\mathcal{R})$，其中包含节点集合$\mathcal{V}$，关系集合$\mathcal{E}$，节点类型集合$\mathcal{N}$以及关系类型集合$\mathcal{R}$.每一个节点$v\in \mathcal{V}$且边$e\in \mathcal{E}$各自地与它们的类型映射函数$\varphi (v):\mathcal{V}\to \mathcal{N}$和$\varphi (e):\mathcal{E}\to \mathcal{R}$相关联。节点的属性$v_i$定义为$x_i\in \mathcal{X}\in {\mathbb{R}}^{\lambda }$.

示例. 图1-(a)显示了一个小的HIN，其中$\mathcal{N}=\{Institution,Author,Paper,Venue\}$且$\mathcal{R}=\{Work,Hire,Write,Written,Cite,Cited,Publish,Published\}$.

定义2.（元路径）： 给定一个HIN $G$，一条元路径$\Omega$用如下形式的序列定义：${\omega }_1\stackrel{r_1}{⟶}{\omega }_2\stackrel{r_2}{⟶}\dots \stackrel{r_n}{⟶}{\omega }_{n+1}$，其中${\omega }_j\in \mathcal{N}$定义的节点类型，$r_i\in \mathcal{R}$定义的关系类型。

示例： 图1-(b)给出了一些元路径示例，例如:$Institution\stackrel{\text{ Hire }}{⟶}Author$，$Venu\stackrel{\text{ Published }}{⟶}Paper\stackrel{\text{ Written}}{⟶}Author$以及$Author\stackrel{\text{ Cite }}{⟶}Author\stackrel{\text{ Write}}{⟶}Paper\stackrel{\text{ Written}}{⟶}Author$.

定义3.(元路径情况): 给定一个HIN $G$的一条元路径$\Omega$，$\Omega$的元路径实例$p$被定义为$G$中遵循$\Omega$定义的模式的节点序列。$P=\{p_1,p_2,\cdots ,p_{n+1}\}$表示生成的元路径$\Omega$实例，其中$p_i\in \mathcal{V}$且$\varphi (p_i)={\omega }_i$对于$1⩽i⩽n+1$成立，以及$\phi \left(⟨p_i,p_{i+1}⟩\right)=r_i$对于$1⩽i⩽n$成立。

示例： 沿着图1-(b)HIN $G$中的元路径$\Omega ：Venu\stackrel{\text{ Published }}{⟶}Paper\stackrel{\text{ Written}}{⟶}Author$，我们在图1-(a)中从$G$中获得了几个元路径实例，例如，$V-2\stackrel{\text{ Published }}{⟶}P-5\stackrel{\text{ Written}}{⟶}A-3$

基于强化学习的异构图表示学习。 给定一个HIN $G=(\mathcal{V},\mathcal{E},\mathcal{N},\mathcal{R})$，异构图表示学习 (HGRL) 的问题旨在学习所有$v_i\in \mathcal{V}$ 的 $d$ 维节点表示 $H[i]\in {\mathbb{R}}^d$，这些表示能够捕获 $G$ 中提供的丰富结构和语义信息。由于$G$的复杂性和异构性，现有的方法是手工设计元路径来表示$G$中的结构和语义，并基于这些元路径学习节点表示。我们的目标是避免手工定义元路径，采用强化学习(Reinforcement
Learning, RL)算法自适应地为每个节点设计合适的元路径，以捕获$G$中全面的结构和语义信息，并使用自动设计的元路径学习有效的节点表示，以释放HGRL的力量。

2.2 马尔可夫决策过程

马尔科夫决策过程(MDP)是描述满足马尔科夫性质[30]的顺序决策过程的数学理想化形式。MDP可以用四元组$(\mathcal{S},\mathcal{A},\mathcal{P},R,)$正式表示，其中$\mathcal{S}$是状态的有限集，$\mathcal{A}$是动作的有限集，$\mathcal{P}$是根据当前观测状态确定下一个动作概率分布的决策策略，由映射函数定义为$\mathcal{P}:\mathcal{S}\times \mathcal{A}\to (0,1)$，更具体地说，策略编码当前状态和动作以输出概率分布$\mathcal{P}\left(a_t\mid s_t\right)$，其中$s_t\in \mathcal{S}$，$a_t\in \mathcal{A}$.奖励函数.$R$定义为$R:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$，用以评估对观测状态$s_t$采取行动$a_t$的结果。

2.3 用强化学习解决MDP

深度强化学习(RL)是一组算法，利用深度神经网络优化MDP。在每个时间步长$t$，RL智能体基于当前状态$s_t\in \mathcal{S}$采取动作$a_t\in \mathcal{A}$，并且观察下一步状态$s_{t+1}$以及奖励$r_t=R(s_t,a_t)$，看一下MDP定义，智能体采取决策策略$\mathcal{P}$.我们的目标是寻找最优决策，使期望折现累积报酬最大化，即:我们想学习一个智能体网络$\pi :\mathcal{S}\to \mathcal{A}$来最大化${\mathrm{E}}_{\pi }\left[{\sum }_{{\mathrm{t}}^{\prime }=\mathrm{t}}^{\mathrm{T}}{\gamma }^{{\mathrm{t}}^{\prime }}{\mathrm{r}}_{{\mathrm{t}}^{\prime }}\right]$，其中$T$是最大的时间步长，$\gamma$是平衡短期和长期收益的折扣因子，低值时更强调即时回报[1]。

现有的RL算法主要分为基于模型和无模型两大类。与基于模型的RL算法相比，无模型的RL算法具有更好的灵活性，因为总是存在模型理解错误的风险，而模型理解错误又会影响学到的策略[1]。我们采用了一种经典的无模型RL算法，即Deep Q-learning (DQN)[22,22]。DQN的基本思想是利用Bellman方程[22]作为交互更新来估计行动-价值函数:
$$Q\left(s_t,a_t;\theta \right)={\mathbb{E}}_{s_{t+1}}\left[R\left(s_t,a_t\right)+\gamma \underset{a_{t+1}}{\max }\left(Q\left(s_{t+1},a_{t+1};\theta \right)\right)\right],\text{\hspace{1em}(1)}$$
其中$s_{t+1}$是下一步的状态，$a_{t+1}$是下一步动作，$\theta$表示神经网络中用于估计决策策略的可训练参数。方程1的命题基于如下直觉:如果对于所有可能的动作$a_{t+1}$，状态$s_{t+1}$的最优值$Q\left(s_{t+1},a_{t+1}\right)$已知，那么最优策略就是选择动作$a_{i+1}$，使期望值$R\left(s_t,a_t\right)+\gamma Q\left(s_{t+1},a_{t+1}\right)$最大化。值迭代算法将覆盖到最优的行动-价值函数，即:$Q\to Q$当$t\to \infty$.

DQN 引入了两种技术来稳定训练：（i）内存缓冲区$\mathcal{D}$，它将智能体在每个时间步长的经验存储在重放内存中，该内存被访问以执行权重更新；(ii)单独的目标$Q-network\hat{Q}$用于生成Q-learning中的目标，并定期更新。将每个存储的经验用于多个更新的能力允许DQN更有效地从其经验中学习，并减少更新的方差。并且，在每数个cupdates之后，我们克隆网络Q，得到一个单独的目标网络$\hat{Q}$，并使用$\hat{Q}$将后续cupdates的Q-learning目标生成为Q，这样波动就不那么剧烈，训练更稳定。

用RL解决HGRL。 正如2.2节所讨论的，HGRL可以被视为MDP，结合本节的内容，我们自然可以利用RL通过解决HGRL的元路径设计过程来优化HGRL。关于使用RL优化HGRL的更多细节可以在下一节中找到。

3 RL-HGNN框架

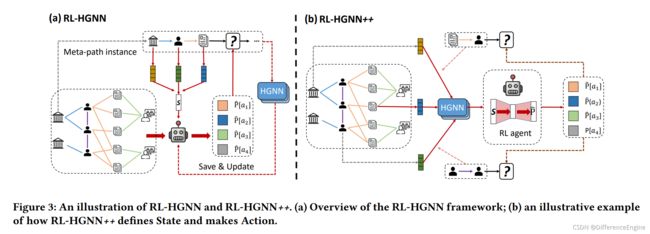
图3-(a)展示了我们的框架RL-HGNN的概述。RL-HGNN中有两个组件，一个是RL智能体模块，一个是HGNN模块。RL 智能体的目的是学习元路径状态与元路径中未来步骤之间的关系。HGNN模块对生成的元路径实例进行信息聚合，以学习节点表示。

图3：RL-HGNN和RL-HGNN++的插图。(a) RL-HGNN框架概述;(b)一个说明RL-HGNN++如何定义状态和采取行动的示例

通过结合这两个模块，我们释放了HGRL的力量，采用RL智能体自适应地为每个节点设计最优的元路径，而不是使用手工定义的元路径。首先，在RL- HGNN中，RL代理将元路径中涉及的节点的属性总结为元路径的状态，并将状态映射为操作(扩展元路径的下一个关系)，如图2所示。接下来，根据元路径生成的元路径实例可以被HGNN模块用来进行信息聚合来更新节点表示。最后，HGNN模块将学习到的节点表示应用于下游任务，并获得更新RL 智能体的奖励分数。

接下来，我们将详细介绍我们的RL-HGNN框架。我们首先描述如何用RL智能体设计元路径以及如何训练RL智能体。然后，我们将展示如何使用设计的元路径执行信息聚合。最后，我们进一步提出了一个RL-HGNN的扩展模型，RL-HGNN++，使元路径设计能够同时探索HIN和HGNN状态的结构语义。此外，它还可以显著加快表示学习过程。

3.1 基于RL的元路径设计

MDP$(\mathcal{S},\mathcal{A},\mathcal{P},R,)$的主要组成部分包括一组状态一组操作、决策策略和奖励功能，如2.2节所述。

如图2所示，具有最大T个时间步长的元路径设计过程可以被建模为T轮决策过程，可以自然地将其视为MDP。我们将起始节点的属性概括为状态，并选择一个关系作为扩展元路径的第一步。在扩展的元路径之后，我们进一步为HGRL生成相应的元路径实例来学习节点表示，这些节点表示可以应用到下游的预测任务中来获得奖励分数。详细地说，我们将元路径设计过程形式化如下。

• 状态$(\mathcal{S})$： 状态用来帮助决策策略选择扩展元路径的关系。捕获现有元路径中的所有有用信息至关重要。因此，我们让状态来记忆元路径中涉及的所有节点。我们以从节点$v_i$开始的元路径$\Omega$为例，在时间步长$t$处，$\Omega$的状态$s_t$正式定义为：
  $$s_t=\frac{\frac{1}{|D(i)|}{\sum }_{j\in D(i)}{x}_j+s_{t-1}}{2},\text{\hspace{1em}(2)}$$

其中$D(i)$表示到达节点在时间步长$t$采取动作$a_t$，$\frac{1}{|D(i)|}{\sum }_{j\in D(i)}{x}_j$表示到达节点的属性在时间步长t的平均值。$s_{t-1}$表示在上一个时间步长$t-1$的状态。请注意$s_0=x_i$.

• 动作$(\mathcal{A})$： 状态$s_t$的操作空间${\mathcal{A}}_t$是HIN中可用关系类型$\{r_0,r_1，\dots \}$的集合，以及一个特殊操作$STOP$。从开始节点$v_i$开始，决策策略迭代预测最有希望扩展当前元路径的关系，以获得更好的奖励分数。要么达到最大的时间步长$T$，要么发现元路径中任何额外的关系都会降低节点表示对下游任务的性能，则决策策略选择动作$STOP$来完成路径设计过程。

• 决策策略$(\mathcal{P})$： MDP的决策策略旨在将$\mathcal{S}$中的一个状态映射到$\mathcal{A}$中的一个动作。在元路径设计过程中，状态空间和动作空间分别是连续空间和离散空间，即$\mathcal{S}⊏{\mathbb{R}}^{\lambda },\mathcal{A}⊏\mathbb{N}$.因此，我们使用深度神经网络来近似动作-价值函数:$\mathcal{P}\left(a_t\mid s_t;\theta \right):\mathcal{S}\times \mathcal{A}\to (0,1)$.另外，由于任意动作$a\in \mathcal{A}$都是正整数，我们使用DQN[22]的Q-network作为决策策略网络，其形式化定义见式1。我们使用MLP[14]作为Q-network的深度神经网络，其定义为:
  $$\begin{array}{rl}{z}_1& =W_1^T{s}_t+c_1\\ z_2& =W_2^T{z}_1+c_2\\ & \dots \\ \hat{P}& =\mathrm{Softmax}\left({\varphi }_m\left(W_m^T{z}_{m-1}+c_m\right)\right)\end{array},\text{\hspace{1em}(3)}$$

其中$W_m$和$c_m$分别表示第$m$层感知器的权值矩阵和偏差向量。输出$\hat{P}\in (0,1)$表示选择不同关系$a\in {\mathcal{A}}_t$来扩展元路径的可能性。需要注意的是，如果其他RL算法能够近似连续状态空间和离散空间，则可以采用其他RL算法作为策略网络。在这里，我们使用一个基本的RL算法来说明我们的框架的主要思想，并证明其有效性。

• 奖励函数$(R)$： 奖励是引导RL智能体的关键因素，我们的目标是设计一个奖励函数来鼓励RL智能体获得更好和稳定的性能。因此，我们将奖励R定义为与历史性能相比，在特定任务上的性能改进。更准确地说，奖励函数被定义为:

$$R\left(s_t,a_t\right)=\mathcal{M}\left(s_t,a_t\right)-\frac{{\sum }_{j=t-b}^{t-1}\mathcal{M}\left(s_j,a_j\right)}{b},\text{\hspace{1em}(4)}$$

$\frac{{\sum }_{j=t-b}^{t-1}\mathcal{M}\left(s_j,a_j\right)}{b}$为时间步长t时的基准性能值，其中包含最后 $b$步的历史表现。$\mathcal{M}(s_t,a_t)$是学习到的节点表示 $H^t[i]$在下游任务上的表现。 在这项工作中，我们采用节点分类作为目标任务，并将其在验证集上的准确性作为评估性能。

最优化。 基于上述定义，本文提出的节点$v_i$在时间步长$t$时的元路径设计过程包括三个阶段:(i)获取时间步长t时的状态$s_t$;(ii)根据当前状态$s_t$，预测一个动作(关系)$a_t=argma{x}_a(\mathcal{Q}(s_t,a;\theta ))$来扩展元路径;(iii)将状态$s_t$更新为$s_{t+1}$。通过对公式1进行优化，训练策略网络Q-函数，其中奖励函数如公式4所定义，损失函数如[22]所定义:
$$\begin{array}{c}{\mathcal{L}}_Q(\theta )={\mathbb{E}}_{\mathcal{T}\sim U(D)}[(R\left(s_t,a_t\right)+\gamma \underset{a_{t+1}}{\max }\hat{Q}\left(s_{t+1},a_{t+1};{\theta }^{-}\right){-Q\left(s_t,a_t;\theta \right))}^2]\end{array},\text{\hspace{1em}(5)}$$
其中$\mathcal{T}=(s_t,a_t,s_{t+1},R_t)$是从内存缓冲区 $\mathcal{D}$中随机采样的回放内存，${\theta }^{-}$是这些平行目标 Q- 网络的参数$\hat{Q}$，${\max }_{a_{t+1}}\hat{Q}\left(s_{t+1},a_{t+1};{\theta }^{-}\right)$为最优目标值$\mathcal{Q}(s_t,a;\theta )$为训练Q-网络的预测值。我们通过反向传播和梯度下降最小化损失函数来优化Q-网络的参数。

3.2 利用元路径进行信息聚合

由于HIN节点的异质性，不同类型的节点具有不同的属性空间。在信息聚合之前，我们首先设计一个特定于节点类型的转换，将不同类型节点的属性投影到同一个属性空间中。预测过程可正式表述如下:
$$H^0[i]=M_{{\omega }_i}\cdot x_i,\text{\hspace{1em}(6)}$$
其中$x_i$和$H^0[i]$为节点$v_i$的原始属性和投影属性，$M_{{\omega }_i}$为${\omega }_i$型节点的变换矩阵。

之后，我们将讨论如何根据这些基于元路径生成的元路径实例执行信息聚合，以学习下游任务的有效节点表示。这里，我们以节点$v_i$为例，$v_i$设计的元路径假设为$\Omega$.

图4：通过元路径实例的信息聚合与我们的无冗余计算的比较(A:作者，P:论文)。(a)从元路径$\Omega :Paper\stackrel{\text{ Written }}{⟶}Author\stackrel{\text{ Cite }}{⟶}Author\stackrel{\text{ Write }}{⟶}Paper$生成的顺序聚合路径实例；(b)通过无冗余计算方法优化的聚合路径。

我们首先按照元路径$\Omega$生成元路径实例$P=\{p_1,p_2,\cdots ,p_{n+1}\}$.如图4所示，可能有许多元路径实例遵循元路径$\Omega$，比如一条元路径$Paper\stackrel{\text{ Written }}{⟶}Author\stackrel{\text{ Cite }}{⟶}Author\stackrel{\text{ Write }}{⟶}Paper$.执行信息聚合的一种直观方法是采用顺序聚合器 [42]。 示例包括 N-ary TreeLSTM [31] 和 GraphSAGE [13] 的 LSTM 变体。 但我们认为这些聚合路径包含计算冗余，可以进一步优化。举例来说，$P_3\to A_2$和$P_5\to A_2$在第一个聚合步骤中反复计算，因此，我们将这两个聚合过程归纳为一个聚合过程$\{P_3,P_5\}\to A_2$，以减少额外的计算，称为无冗余信息聚合。此外，我们还为每个聚合路径添加了注意值$Att(s,j)$，以区分不同的路径实例[34]。我们在第4.7节中进行了实证研究，以比较使用和不使用这种无冗余优化的聚合数量。设$H^t[i]$为节点$v_i$的学习表示，$\hat{H}[j]$为时间步长$t$参与$P$的节点$v_j$的表示，我们首先将$\hat{H}[j]$的更新过程形式化描述为:
$${\hat{H}}^l[j]=\underset{s\in N(j)}{\mathrm{Aggregate}}\left(Att(s,j)\cdot {\hat{H}}^{l-1}[j]\right),\text{\hspace{1em}(7)}$$
其中$N(j)$包括$P$中$v_j$的连通节点，$l\in \{1,2,\cdots ,t\}$是执行信息聚合的聚合器id，并且${\hat{H}}^0[j]=H^0[j]$.同样地，$H^t[i]$也可以通过公式7学习$t $个聚合器堆叠在一起形成我们的 HGNN，它可以在时间步 $t $用 $t$次聚合更新节点表示。

两个基本运算符$Att(\cdot )$和$Aggregate(\cdot )$定义为:
$$\begin{array}{c}\mathrm{Att}(s,j)=\underset{s\in N(j)}{\mathrm{Softmax}}\left(\mathrm{Leakrelu}\left(W{\hat{H}}^{l-1}[s]\Vert W{\hat{H}}^{l-1}[j]\right)\right)\\ \text{ Aggregate }(\cdot )=\mathrm{Relu}(\mathrm{Mean}(\cdot ))\end{array},$$
其中$W$包含可训练参数。使用 $Att(·) $可以帮助我们在最优聚合机制中区分不同的路径实例。例如，两个元路径实例:
$P_3\underset{{\mathrm{A}\mathrm{t}\mathrm{t}}_1}{\stackrel{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}}{⟶}}{A}_2\underset{{\mathrm{A}\mathrm{t}\mathrm{t}}_3}{\stackrel{\mathrm{C}\mathrm{i}\mathrm{t}\mathrm{e}}{⟶}}{A}_1$以及$P_3\underset{{\mathrm{A}\mathrm{t}\mathrm{t}}_1}{\stackrel{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}}{⟶}}{A}_2\underset{{\mathrm{A}\mathrm{t}\mathrm{t}}_4}{\stackrel{\mathrm{C}\mathrm{i}\mathrm{t}\mathrm{e}}{⟶}}{A}_3$，即使它们的前半部分被整合在一起，但注意力分数有助于区分它们。

参数共享。 我们通过参数共享机制减少了训练参数的数量。 特别是，我们首先在开始时初始化 HGNN 的最大时间步$T$，在每个时间步中，我们按照动作 $a_t$的初始化顺序重复堆叠聚合器以执行信息聚合。 这样，如果每个聚合器的可训练参数个数为 $u$，我们只需要训练$T\times u$个参数，而不是 $\frac{T\times (T+1)}{2}\times u$个参数。

HGNN的训练。 最后，更新后的节点表示 $H^t[i]$可以应用于下游任务并设计不同的损失函数来更新 HGNN。 对于半监督节点分类，在一小部分标记节点的帮助下，我们可以通过反向传播和梯度下降最小化交叉熵来优化 HGNN 的参数。 交叉熵损失可以正式定义为：
$$\mathcal{L}=-\sum _{v\in {\mathcal{V}}_L}\sum _{c=0}^{C-1}{y}_v[c]\cdot \log \left(H^t[v][c]\right),\text{\hspace{1em}(8)}$$
其中${\mathcal{V}}_L$表示带有标签的节点集合，$C$是类的数量，$y_v$是节点$v$的one-hot标签向量，$H^t[i]$是节点$v$的学习节点表示向量。同时，学习到的节点表示可以通过任务特定的评估矩阵$M_{eval}$进行评估，并输入到公式 4即$\mathcal{M}(s_t,a_t)=M_{eval}(H^t)$中以获得奖励分数。 我们在算法 1 中总结了我们的 RLHGNN 框架。

3.3 RL-HGNN++

从前面的章节可以看出，RL- HGNN主要采用RL智能体对HGRL进行自适应的元路径设计。然而，回顾图5-(a)和算法1所示的RL-HGNN的整体工作流程，我们发现有三个局限性:(i)忽略了HGNN随机性对HGRL的影响;(ii)在设计元路径时忽略了HIN的结构;(iii) HGNN需要大量的轮数来训练其参数并获得节点表示，这限制了RL-HGNN的效率。更具体地说，RL-HGNN设计元路径时只考虑来自HIN的节点属性信息，即状态$s_t$汇总元路径中涉及的节点属性。然而，学习到的节点表示的质量也与 HGNN 密切相关，但到目前为止 RL-HGNN 没有考虑到这一点。 例如，Scardapane 和 Wang [24] 讨论了深度神经网络模型的随机性，并展示了可能影响模型性能的各种随机因素。 此外，与其他深度神经网络的训练过程类似，RL-HGNN 的编码器需要多轮来训练其参数，以根据一组元路径实例学习有效的节点表示。通过这种方式，如果HGNN需要$B$轮训练得到参数，那么我们需要$T\times B$轮来完成最大$T$时间步长的元路径设计过程。同时，RL 智能体还需要大量四元组样本$\left(\mathcal{T}=\left(s_t,a_t,s_{t+1},R_t\right)\right)$来训练策略网络，这可能导致组合规模爆炸。

图5:RL-HGNN和RL-HGNN++工作流程概述。(a) RL-HGNN的工作流程:RL 智能体根据节点属性信息为HIN节点设计元路径，然后使用设计的元路径训练HGNN模型，并使用训练的HGNN学习节点表示。奖励分数可以通过在下游任务上应用学到的表示来获得，然后可以用来更新RL代理。(b)RL-HGNN++的工作流程:RL
智能体根据HIN的结构和语义信息以及HGNN的状态为HIN的节点设计元路径，然后通过HGNN学习节点表示。学习到的表示可以用于优化HGNN和更新RL
智能体后，应用到下游任务。

新状态$(\mathcal{S})$： 为了解决已识别的局限性，我们提出了 RL-HGNN 的扩展，它可以利用 HIN 和 HGNN 模块的综合信息。 我们的解决方案是定义一个新的状态来捕获此类信息。 特别地，我们利用元路径起始节点 $v_i$的最新节点表示向量 $H^{t-1}[i]$ 作为状态。 按照这种方式，在HGNN的帮助下将结构和节点属性信息汇总在$H^{t-1}[i]$中，同时HGNN的状态也反映在$H^{t-1}[i]$中。 新状态$(\mathcal{S})$可以形式化描述为：
$$s_t=\text{ Normalise }\left(H^{t-1}[i]\right),\text{\hspace{1em}(9)}$$
其中 $Normalize$ 是在前 $B$ 个生成状态上训练的归一化器，用于将状态转换为相同的分布。 请注意，规范化是深度强化学习算法中常用的一种技巧，用于在状态空间非常稀疏时稳定训练。

新的训练过程。 根据新的状态定义，训练过程也可以进一步优化。新工艺如图5-(b)所示。与RL-HGNN的过程相比(如图5-(a)所示)，主要的区别在于我们可以直接利用HGNN学习有效的节点表示，而不是在通过元路径学习节点表示之前用完整的训练过程更新HGNN。学习的节点表示可以进一步用于优化HGNN的参数和更新RL智能体。这是因为元路径是为HGNN的当前状态而设计的。在这种新颖的训练过程中，我们只需要$T$轮就可以完成元路径设计过程，而不是$T\times K$轮。我们对4.7节中RL-HGNN和RL-HGNN++的耗时进行了实证分析。在算法2中总结了RL-HGNN++。

4 实验

我们通过实验对RL-HGNN和RL-HGNN++进行评估，解决以下研究问题:

RQ1：与最先进的HGRL模型相比，RL-HGNN和RL-HGNN++表现如何?

RQ2：RL-HGNN探索的元路径和人类设计的元路径之间的主要区别是什么?

RQ3：RL-HGNN的主要组成部分有什么影响?

4.1 数据集

我们采用来自不同领域的两个广泛使用的HIN数据集来评估我们的模型的性能。数据集的详细描述如表1所示。

表1：数据集统计。

注：IMDB和DBLP的数据来源分别为https://www.imdb.com/和https://dblp.uni-trier.de/

• IMDB是一个关于电影和电视节目的在线数据集，包括演员、制作人员和情节摘要等信息。 我们提取了 IMDB 的一个子集，其中包含 4,278 部电影、2,081 位导演和 5,257 位演员。 电影根据其类型信息被标记为三个类别之一，即动作、喜剧和戏剧。 每部电影的特征对应于词袋的元素（即它们的情节关键词，总共 1,232 个）。
• DBLP 是一个在线计算机科学参考书目。 我们提取 DBLP 的一个子集，其中包含 4,057 部影像、1,4328 篇论文、7,723 个术语和 20 个场所。 作者被标记为以下四个研究领域之一：数据库、数据挖掘、机器学习和信息重试。 每个作者都可以用一个词袋来描述（即他们的论文关键词，总共 334 个）。

4.2 竞争方法

为了验证所提出的模型的有效性，我们比较了它们与不同类型的最先进的模型的性能，包括5个同质图表示学习模型和7个异质图表示学习模型:

• LINE[32] 是一个利用节点之间一阶和二阶接近度的同构模型。 我们通过忽略 HIN 异质性和节点属性将其应用于数据集。
• DeepWalk[23] 是一种基于随机游走的同构图表示学习方法，我们通过忽略 HIN 异质性和节点属性将其应用于数据集。
• ESim[27] 是一种HGRL 方法，它从多个元路径中学习不同的语义。它需要为每个元路径预定义权重，我们为所有元路径分配相同的权重。
• metapath2vec[6] 是一种HGRL 方法，它在预定义元路径的指导下对HIN 执行随机游走，并利用skip-gram 生成节点表示。 •HERec[28] 是一种HGRL 方法，它设计了一种类型约束策略来过滤节点序列并利用skip-gram 生成节点表示。
• MLP[14] 是一类前馈神经网络，它从没有结构信息的节点属性中学习信息。
• GCN[19] 是一个同构的 GNN，将卷积操作扩展到图。
• GAT[34] 是一个同构 GNN，它使用注意力机制在图上执行卷积。
• RGCN[25] 是一个异构的 GNN 模型，它为每个关系保持不同的权重以在图上执行卷积。
• HAN[38] 是一个异构 GNN 模型，它从不同的基于元路径的同构图中学习元路径引导节点表示，并将它们与使用注意力集成。
• MAGNN[10] 是一个异构的 GNN 模型，它定义了元路径实例编码器来提取元路径中的结构和语义，以改进生成的表示。
• HGT[16] 是一个异构的GNN 模型，它使用每个元关系来参数化类似transformer 的self-attention 架构，以捕获常见和特定的关系模式。

4.3 实现细节

对于提出的的 RL-HGNN 和 RL-HGNN++ 的 DQN，我们使用 [20] 中的实现，并进行了一些修改以使其适合我们的模型。 我们开发了 5 层 MLP，其中 (32,64,128,64,32) 作为 $\mathcal{Q}$ 函数的隐藏单元。 内存大小为 $50\times b$，其中 $b$ 是数据集中验证节点的数量。 对于提出的 RL-HGNN 和 RL-HGNN++ 的 HGNN 模型，我们随机初始化参数并使用 Adam 优化器优化模型 [18]。 我们将学习率设为 0.005，正则化参数设为 0.0001，表示向量维度为 128，注意力向量 $Att(\cdot )$ 维度设为 16，训练批次大小设为 256，attention head数量为 8， dropout ratio达到 0.5。 IMDB 和 DBLP 的最大时间步长$(T)$分别为 2 和 4。 代码和数据可见：https://github.com/zhiqiangzhongddu/RLHGNN .

对于基于随机游走的竞争方法，包括 DeepWalk、Esim、metapath2vec 和 HERec，我们将窗口大小设置为 5，步行长度为 100，每个节点的步行次数为 40，负样本数为 5。对于元路径引导的竞争方法 ，包括 Esim、metapath2vec、HERec、HAN 和 MAGNN，我们为它们提供了预定义的元路径，如 [38] 中所述。对于IMDB，有两条元路径:$Movie\stackrel{M-A}{⟶}Actor\stackrel{A-M}{⟶}Movie$和$Movie\stackrel{M-D}{⟶}Director\stackrel{D-M}{⟶}Movie$.对于DBLP，有三条元路径:$Author\stackrel{A-P}{⟶}Paper\stackrel{P-A}{⟶}Author$，$Author\stackrel{A-P}{⟶}Paper\stackrel{P-T}{⟶}Term\stackrel{T-P}{⟶}Paper\stackrel{P-A}{⟶}Author$和$Author\stackrel{A-P}{⟶}Paper\stackrel{P-V}{⟶}Venue\stackrel{V-P}{⟶}Paper\stackrel{P-A}{⟶}Author$.对于基于GNN的模型，我们在相同的数据分割上使用与RL-HGNN相同的参数进行测试。我们按照作者的官方代码在$\text{PyG}$中重新实现所有竞争模型。

注：实现链接为https://pytorch-geometric.readthedocs.io/en/latest/

4.5 实验结果(RQ1)

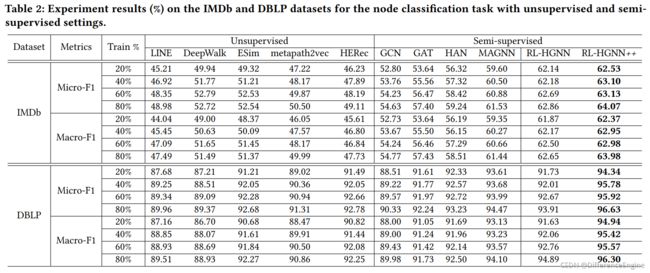
半监督节点分类。 我们在表 2 中展示了半监督节点分类的结果，其中不支持半监督设置的竞争方法保留其无监督设置。我们报告了每个模型不同种子的 10 次运行的平均 Micro-F1 和 Macro-F1。如表所示，RL-HGNN++ 在不同比例和数据集上的表现始终优于其他竞争方法。在 IMDB 上，RL-HGNN++ 比最佳竞争方法 (MAGNN) 获得的性能提升约为 (3.7% - 5.08%)。并且对于GNN，包括为同构和异构图设计的所有 GNN 模型，其性能优于浅层异构网络嵌入模型，这表明异构节点属性的使用显着提高了性能。在 DBLP 上，与 IMDB 上的结果相比，所有模型的性能总体上更好。有趣的是，与 IMDB 上的结果不同，浅层异构网络方法获得了比同类 GNN 更好的性能。也就是说，DBLP 上的异构关系对于节点分类任务很有用。 RL-HGNN++ 优于最强的竞争方法高达 2.4%，它展示了 RL-HGNN++ 的通用性。

此外，我们还有一个有趣的观察结果，即 RLHGNN 在大多数情况下在 IMDB 数据集上的表现优于竞争方法，但在大多数情况下在 DBLP 数据集上的表现不如最强基线。 我们认为原因是 DBLP 数据集中的标签比 IMDB 中的标签更准确，而 DBLP 包含更丰富的异构关系。 由于 RL-HGNN 只能为每个节点生成一个元路径，与具有许多人为定义的元路径的基线相比，这是不够的。 相比之下，RL-HGNN++ 可以在两个数据集上达到最佳性能，这要归功于其定义具有全面信息的元路径的设计。

表2：在IMDb和DBLP数据集上对无监督和半监督设置的节点分类任务的实验结果(%)。

监督节点分类。 我们在表 3 中展示了监督节点分类的结果。 我们报告了具有不同种子的每个模型 10 次运行的平均 Micro-F1 和 Macro-F1。 对于该表，我们可以看到 RL-HGNN++ 在 IMDB 和 DBLP 数据集上始终优于所有竞争模型，在 Micro-F1 方面高达 5.6%。 请注意，所有包含拓扑信息的 GNN 模型都比仅适用于节点属性的 MLP 获得更好的性能。 异构 GNN 优于同类 GNN，我们的 RL 增强模型 RL-HGNN++ 实现了最佳性能。 这证明了异构关系的有用性以及根据每个节点的特征为每个节点设计不同的适当元路径的优势。

表3:有监督设置的节点分类任务在IMDb和DBLP数据集上的实验结果(%).

4.6 元路径分析(RQ1)

除了对我们提出的框架的定量评估之外，我们还可视化了 RL 智能体如何为每个节点设计元路径以回答 RQ2 的过程。 如图 6 所示，它总结了 RL 智能体在不同最大时间步长下在 IMDB 上所做的动作。 他们遵循半监督训练设置，并注意到由于 RL-HGNN++ 可能会在不同的轮次中生成不同的元路径，这里我们只展示达到最佳验证性能的轮次的动作。 有趣的是，RL 智能体在第一个时间步比另一个 $M-D$ 更频繁地选择关系 $M-A$，这意味着电影的特征与其演员的关系比其导演更相关。 此外，当时间步长 $t=2$ 时，RL 智能体选择越来越多的 $STOP$ 动作（在图 6 中表示为${}^{\prime }{S}^{\prime }$）。这表明了两个短元路径，即，:$Movie\stackrel{M-A}{⟶}Actor$以及$Movie \stackrel{M-D}{\longrightarrow} Director $已经足够让主要节点学习它们的有效表示。此外，有 6.7%-9,4% 的节点不需要任何元路径来学习它们的表示，这意味着它们的属性可以提供足够的信息。 这也反映在第 4.5 节的 MLP 的结果中，它不利用任何结构信息，只利用节点属性。

图6 RL 智能体在IMDB上的作用细化:(a)、(b)、©分别对应于最大时间步长T=1、T=2、T=3的RL- HGNN++.线条的粗细表示相应动作的比例。

此外，我们在 RL-HGNN++ 生成的 表4中展示了最相关的元路径，具有不同的最大时间步长 $T$。 与图 6 类似，这里我们仅展示达到最佳验证性能的回合的元路径。 从表中，我们可以发现 RL 智能体能够为不同的节点设计各种元路径。 手动定义的元路径，即$Movie\stackrel{M-A}{⟶}Actor\stackrel{A-M}{⟶}Movie$也被我们的模型发现。 然而，这些由专家定义的元路径对于学习电影节点的节点表示并不是最有用的。相反，有两条短的元路径$Movie\stackrel{M-A}{⟶}Actor$以及$Movie\stackrel{M-D}{⟶}Director$是最有用的。这表明电影的参与者(导演和演员)很大程度上决定了电影的类型(因为目标任务是预测电影的类别)。

图4：IMDB中RL-HGNN++设计的元路径。

注：我们在表4中省略了所有元路径的关系类型。

此外，考虑到RL-HGNN++ 在不同最大时间步长$(T)$下的性能，如图7所示，$T\ge 2$与$T=1$相比，性能有显著提高，我们认为具有更丰富语义的元路径可以带来学习更好的节点表示的好处。最后，RL-HGNN++设计了一些被专家忽略的元路径，如:$Movie\stackrel{M-A}{⟶}Actor\stackrel{A-M}{⟶}Movie\stackrel{M-A}{⟶}Actor$，它们比$Movie\stackrel{M-A}{⟶}Actor\stackrel{A-M}{⟶}Movie$更有效。

图7：在不同的最大时间步长下，RL-HGNN++在IMDB上的性能(根据Micro F1)和聚集数量。

4.7 模型分析(RQ3)

我们进行实验来研究超参数的影响并评估 RL-HGNN 中某些组件的有效性。

最大时间步长$T$ 的影响。 在半监督节点分类中，我们遵循相同的实验程序，研究一个关键超参数，即最大时间步长 $T$的影响。 具体来说，我们研究以下两个方面：（i）它对 Micro F1测量的分类任务的性能； (ii) 它对信息聚合数量的影响。 结果如图 7 所示。我们可以看到，$T\ge 2$的情况在 Micro F1 方面比 $T=1$有显着的改进，并且随着$T$ 的增加，信息聚合的数量也增加了。 考虑到更多的信息聚合会导致更高的计算成本，我们为第 4.5 节中的所有实验选择 $T=2$，即使 $T>2$ 可以带来更好的性能。

无冗余优化的影响。 在这里，我们通过比较有和没有优化的信息聚合的数量来研究无冗余优化的影响。 图 8 显示了比较结果。 我们可以发现这种优化策略显着减少了信息聚合的数量。 此外，随着最大时间步长 T 的增加，减少的比率变得更高。 例如，优化在$T=2$ 时减少了 IMDB 上大约 50% 的聚合，当 $T=4$时减少的比例超过 80%。

图8:用不同的最大时间步长比较有无冗余优化的聚合数量(越低越好)。

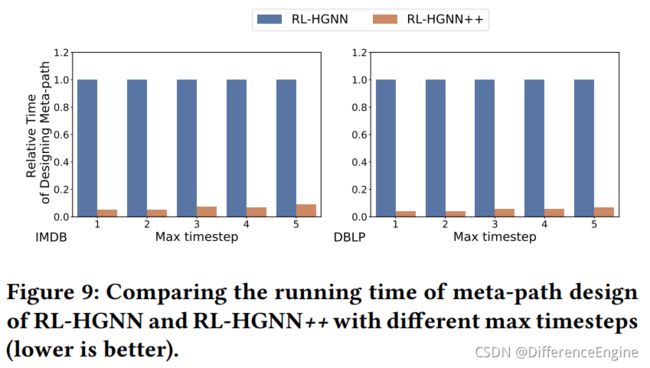
元路径设计的耗时比较。 正如我们在第 3.3 节中介绍的那样，RL-HGNN++ 通过优化训练过程显着加快了元路径设计过程。 在这里，我们对 RL-HGNN 和 RL-HGNN++ 元路径设计的耗时进行了比较。 我们计算RL-HGNN++相对于RL-HGNN的运行时间，结果如图9所示。 从图中我们可以发现，RL-HGNN++在两个数据集上消耗的时间都不到 RL-HGNN 运行时间的 5%。

图9:RL-HGNN和RL-HGNN++在不同最大时间步长的情况下元路径设计的运行时间比较(越低越好)

5 相关工作

图神经网络。 现有的图神经网络 (GNN) 将深度神经网络的卷积运算泛化到处理任意图结构数据 [40]。通常，GNN 模型可以被视为使用输入图结构生成节点的消息传递计算图 [11]，在此期间聚合局部邻域信息以获得网络中节点的更上下文表示。遵循这个想法，首先提出了基于谱的 GNN 模型来在图的傅立叶域中执行图卷积 [3,5]。德弗拉德等人。提出了 ChebNet，它利用 Chebyshev 多项式来过滤图中的节点特征 [5]。后来，另一系列空间方法因其有效性和效率而引起了极大的关注 [13,19,34,41]。基于空间的 GNN 模型通过从每个节点的邻居中聚合节点特征并进一步结合其自身特征，直接在图域中定义卷积。对于信息聚合，GCN [19] 采用均值池化，GraphSAGE [13] 将节点的特征与补充的 max/LSTM [15] 池化邻居信息连接起来。受 Transformer [33] 的启发，GAT [34] 基于可训练的注意力权重聚合邻域信息。已经提出了其他几种基于空间的 GNN 变体来进一步扩展这个想法。 DGI [35] 或者通过最大化局部互信息来驱动局部网络嵌入以捕获全局结构信息。 Cluster-GCN [4] 使用图聚类算法对子图进行采样，并对采样的子图中的节点进行图卷积，以提高处理大图的能力。

然而，现实世界中复杂的图结构数据通常与多种类型的对象和关系相关联。上述GNN模型均假定图是齐次的，因此很难直接应用到HINs中。

异构图表示学习。 HGRL 旨在将 HIN 中的节点投影到低维向量空间，同时保留异构节点的特征和关系。最近的一项调查对 HGRL [7] 进行了全面概述，它侧重于浅层异构网络嵌入方法 [6,8,9]，以及由相当复杂的深度编码器提供支持的基于异构 GNN 的方法 [10,16,25] ,38,42]。 “浅”方法的特点是一个嵌入查找表，这意味着它们直接将网络中的每个节点编码为一个向量，这个嵌入表就是要优化的参数。例如，Metapath2vec [6] 设计了一个基于元路径的随机游走，并利用 skip-gram [2] 来执行异构图嵌入。 HIN2Vec [9] 执行多个预测训练任务，同时学习节点和元路径的潜在向量。然而，Metapath2vec 和 HIN2Vec 只利用了少数元路径，它们都不能利用节点属性，也不支持端到端的训练策略。另一方面，受 GNN 模型最近出色表现的启发，一些研究试图将 GNN 扩展到 HIN。 R-GCNs 模型为每种关系类型保持不同的线性投影权重 [25]。 HetGNN [42] 针对不同的节点类型采用不同的循环神经网络来集成多模态特征。 HAN [38] 通过为不同的元路径定义的边维护不同的权重来扩展 GAT，而 MAGNN [10] 定义了元路径实例编码器，用于提取元路径实例中根深蒂固的结构和语义信息。

然而，所有这些模型都需要人工和领域专业知识来定义元路径，以捕获给定异构结构背后的语义。 这导致了两个主要限制：（i）元路径的设计需要丰富的领域知识，而这在复杂且语义丰富的 HIN 中极难获得； (ii) 现有的元路径引导方法简单地假设相同类型的不同节点/关系共享相同的元路径，而忽略了各个节点之间的差异。 最近提出的一个模型 HGT [16] 试图通过设计可转移关系分数来避免对人类定义的元路径的依赖，但其探索范围受到 HGNN 模型层数的限制，并且引入了大量的 要优化的参数。 因此，我们打算设计一个新的 HGRL 框架，它在强化学习的帮助下为网络中的每个节点自适应地设计不同的元路径。

6 结论和未来工作

我们在本文中研究了异构图表示学习（HGRL）问题，并确定了现有 HGRL 方法的局限性，主要是由于它们依赖于手动定义的元路径。 为了充分发挥 HGRL 的威力，我们提出了一种新的框架强化学习增强异构图神经网络（RL-HGNN），并提出了一个扩展模型 RL-HGNN++。 与现有的 HGRL 模型相比，我们框架的最大改进是避免了手动定义 HGRL 的元路径。 实验结果表明，我们的框架通常优于竞争方法，并发现了许多被人类设计忽略的有用元路径。

未来，我们的目标是采用多智能体 RL 算法，进一步使 RL-HGNN 能够为每个节点设计多个元路径，而不是只关注一个最优元路径。 此外，研究如何将我们的框架扩展到 HIN 上的其他任务也很有趣，例如在线推荐系统、知识图补全等。

致谢

这项工作得到了卢森堡国家研究基金的资助，PRIDE15/10621687/SPsquared。 这项工作还得到了台湾科学技术部 (MOST) 的资助 109-2636-E-006-017（MOST 青年学者奖学金）和 108-2218-E-006-036，以及中央研究院在 授予 AS-TP-107-M05。 作者感谢Zhe Xie 对代码设计的帮助。

参考文献

[1]Kai Arulkumaran, Marc Peter Deisenroth, Miles Brundage, and Anil Anthony Bharath. 2017. Deep Reinforcement Learning: A Brief Survey.IEEE Signal Processing Magazine(2017).

[2]Antoine Bordes, Nicolas Usunier, Alberto García-Durán, Jason Weston, and Oksana Yakhnenko. 2013. Translating Embeddings for Modeling Multirelational Data. InProceedings of the 2013 Annual Conference on Neural Information Processing Systems(NeurIPS). NeurIPS, 2787–2795.

[3]Joan Bruna, Wojciech Zaremba, Arthur Szlam, and Yann LeCun. 2014. Spectral Networks and Locally Connected Networks on Graphs. InProceedings of the 2014 International Conference on Learning Representations (ICLR).

[4]Wei-Lin Chiang, Xuanqing Liu, Si Si, Yang Li, Samy Bengio, and Cho-Jui Hsieh. 2019. Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks.
InProceedings of the 2019 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 257–266.

[5]Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. 2016. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering… In Proceedings of the 2016 Annual Conference on Neural Information Processing Systems (NeurIPS). NeurIPS, 3837–3845.

[6]Yuxiao Dong, Nitesh V. Chawla, and Ananthram Swami. 2017. metapath2vec: Scalable Representation Learning for Heterogeneous Networks. InProceedings of the 2017 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 135–144.

[7]Yuxiao Dong, Ziniu Hu, Kuansan Wang, Yizhou Sun, and Jie Tang. 2020. Heterogeneous Network Representation Learning. InProceedings of the 2020 International Joint Conferences on Artifical Intelligence (IJCAI). IJCAI, 4861–4867.

[8]Yujie Fan, Shifu Hou, Yiming Zhang, Yanfang Ye, and Melih Abdulhayoglu. 2018. Gotcha - Sly Malware!: Scorpion A Metagraph2vec Based Malware Detection System. InProceedings of the 2018 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 253–262.

[9]Tao-Yang Fu, Wang-Chien Lee, and Zhen Lei. 2017. HIN2Vec: Explore Metapaths in Heterogeneous Information Networks for Representation Learning. InProceedings of the 2017 ACM International Conference on Information and Knowledge Management (CIKM). ACM, 1797–1806.

[10]Xinyu Fu, Jiani Zhang, Ziqiao Meng, and Irwin King. 2020. MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph embedding. In Proceedings of the 2020 International Conference on World Wide Web (WWW). ACM, 2331–2341.

[11]Justin Gilmer, Samuel S. Schoenholz, Patrick F. Riley, Oriol Vinyals, and George E. Dahl. [n.d.]. Neural Message Passing for Quantum Chemistry.

[12]Aditya Grover and Jure Leskovec. 2016. node2vec: Scalable Feature Learning for Networks. InProceedings of the 2016 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 855–864.

[13]William L. Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. InProceedings of the 2017 Annual Conference on Neural Information Processing Systems (NeurIPS). NeurIPS, 1025–1035.

[14]Simon Haykin. 1999. Neural Networks: A Comprehensive Foundation.Knowledge Engineering Review(1999).

[15]Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long short-term memory.Neural computation(1997).

[16]Ziniu Hu, Yuxiao Dong, Kuansan Wang, and Yizhou Sun. 2020. Heterogeneous Graph Transformer. InProceedings of the 2020 International Conference on World Wide Web (WWW). ACM, 2704–2710.

[17]Jiarui Jin, Jiarui Qin, Yuchen Fang, Kounianhua Du, Weinan Zhang, Yong Yu, Zheng Zhang, and Alexander J. Smola. 2020. An Efficient Neighborhood-based Interaction Model for Recommendation on Heterogeneous Graph. InProceedings of the 2020 ACM Conference on Knowledge
Discovery and Data Mining (KDD). ACM, 75–84.

[18]Diederik P. Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. InProceedings of the 2015 International Conference on Learning Representations (ICLR).

[19]Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. InProceedings of the 2017 International Conference on Learning Representations (ICLR).

[20]Kwei-Herng Lai, Daochen Zha, Kaixiong Zhou, and Xia Hu. 2020. Policy-GNN: Aggregation Optimization for Graph Neural Networks. InProceedings of the 2020 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 461–471.

[21]Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin A. Riedmiller. 2013. Playing Atari with Deep Reinforcement Learning.CoRR abs/1312.5602(2013).

[22]Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness, Marc G. Bellemare, Alex Graves, Martin A. Riedmiller, Andreas Fidjeland, Georg Ostrovski, Stig Petersen, Charles Beattie, Amir Sadik, Ioannis Antonoglou, Helen King, Dharshan Kumaran, Daan Wierstra, Shane Legg, and Demis Hassabis. 2015.Human-levelcontrol through deep reinforcement learning.Nature518 (2015), 529–533.

[23]Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. 2014. DeepWalk: Online learning of social representations. InProceedings of the 2014 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 701–710.

[24]Simone Scardapane and Dianhui Wang. 2017. Randomness in neural networks: an overview.Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery (2017).

[25]Michael Sejr Schlichtkrull, Thomas N. Kipf, Peter Bloem, Rianne van den Berg, Ivan Titov, and Max Welling. 2019. Modeling Relational Data with Graph Convolutional Networks. InEuropean Semantic Web Conference (ESWC). ACM, 593–607.

[26]Dominic Seyler, Praveen Chandar, and Matthew Davis. 2018. An Information Retrieval Framework for Contextual Suggestion Based on Heterogeneous Information Network Embeddings. InProceedings of the 2018 International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR). ACM, 953–956.

[27]Jingbo Shang, Meng Qu, Jialu Liu, Lance M. Kaplan, Jiawei Han, and Jian Peng. 2016. Meta-Path Guided Embedding for Similarity Search in Large-Scale Heterogeneous Information Networks.CoRR abs/1610.09769(2016).

[28]Chuan Shi, Binbin Hu, Wayne Xin Zhao, and Philip S. Yu. 2019. Heterogeneous Information Network Embedding for Recommendation.IEEE Transactions on Knowledge and Data Engineering(2019).

[29]Yizhou Sun and Jiawei Han. 2012. Mining heterogeneous information networks: a structural analysis approach.ACM SIGKDD Explorations Newsletter(2012).

[30]Richard S. Sutton and Andrew G. Barto. 1998.Reinforcement learning - an introduction. MIT Press.

[31]Kai Sheng Tai, Richard Socher, and
Christopher D. Manning. 2015. Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks. InProceedings of the 2015 Annual Meeting of the Association for Computational Linguistics (ACL). ACL, 1556–1566.

[32]Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. 2015. LINE: Large-scale Information Network Embedding. InProceedings of the 2015 International Conference on World Wide Web (WWW). ACM, 1067–1077.

[33]Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is All you Need. InProceedings of the 2017 Annual Conference on Neural Information Processing Systems (NeurIPS). NeurIPS, 5998–6008.

[34]Petar Velickovic, Guillem
Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. 2018. Graph attention networks. InProceedings of the 2018 International Conference on Learning Representations (ICLR).

[35]Petar Velickovic, William Fedus, William L. Hamilton, Pietro Liò, Yoshua Bengio, and R. Devon Hjelm. 2019. Deep Graph Infomax. InProceedings of the 2019 International Conference on Learning Representations (ICLR).

[36]Xuan-Son Vu, Addi Ait-Mlouk, Erik Elmroth, and Lili Jiang. 2019. Graph-based Interactive Data Federation System for Heterogeneous Data Retrieval and Analytics. InProceedings of the 2019 International Conference on World Wide Web (WWW). ACM, 3595–3599.

[37]Guojia Wan, Bo Du, Shirui Pan, and
Gholamreza Haffari. 2020. Reinforcement Learning Based Meta-Path Discovery in Large-Scale Heterogeneous Information Networks. InProceedings of the 2020 AAAI Conference on Artificial Intelligence (AAAI). AAAI.

[38]Xiao Wang, Houye Ji,
Chuan Shi, Bai Wang, Yanfang Ye, Peng Cui, and Philip S. Yu. 2019. Heterogeneous Graph Attention Network. InProceedings of the 2019 International Conference on World Wide Web (WWW). ACM, 2022–2032.

[39]Xin Wang, Ying Wang, and Yunzhi Ling. 2020. Attention-Guide Walk Model in Heterogeneous Information Network for Multi-Style Recommendation Explanation. InProceedings of the 2020 AAAI Conference on Artificial Intelligence (AAAI). AAAI, 6275–6282.

[40]Zonghan Wu, Shirui Pan, Fengwen Chen, and Guodong Long. 2020.A Comprehensive Survey on Graph Neural Networks.IEEE Transactions on Neural Networks and Learning Systems(2020).

[41]Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2019. How Powerful are Graph Neural Networks?. InProceedings of the 2019 International Conference on Machine Learning (ICML). JMLR.

[42]Chuxu Zhang, Dongjin Song, Chao Huang, Ananthram Swami, and Nitesh V.Chawla.2019.Heterogeneous Graph Neural Network. InProceedings of the 2019 ACM Conference on Knowledge Discovery and Data Mining (KDD). ACM, 793–803.