基于kd树的k近邻算法——KNN

1、简介

k近邻算法是机器学习中一种基本的分类与回归算法，对你没听错k近邻算法不仅可以用来做分类，还可以用于回归，英文全称为k-Nearest Neighbor简称k-NN。k近邻算法属于一种有监督学习算法，不同于决策树、感知机等常见的有监督学习分类算法，决策树和感知机都有一个基于已标记的训练样本进行训练的过程，后续基于训练得到的模型进行归类预测，而k近邻算法作为一种有监督学习算法，虽然同样需要已标记的训练样本，但并没有一个显示的学习过程，也不会获得相应的模型用于后续预测，或者说k近邻算法的模型就是训练样本本身，k近邻算法的这个特点是由其分类思想所决定的。

2、分类思想

k近邻算法用于分类基于这样一种假设：越接近的两个个体，它们的属性就越相似，属于同一类别的可能性也就越高。
据此k近邻算法的分类流程如下：对于一个类别未知的样本，基于某种相似性评价策略，从类别已知的训练样本中找出k个与待分类样本最相似最接近的样本，对这k个样本的类别进行统计，找出样本数最多的那个类别作为待分类样本的最终类别，流程图如下：

由于每一个输入样本都有k个不同的最相似样本，因此也就无法事先通过已标记的样本进行训练得到相应的模型用于后续分类

3、三要素

k值得选择、样本间的相似性评价策略、分类决策规则被称为k近邻算法三要素。在三要素确定的情况下，对于每一个输入的待分类样本基于已标记的训练样本都有唯一确定的类别。从某种程度上将，k近邻算法可以看作一种空间分割算法，基于三要素对训练样本所在的特征空间进行划分，将特征空间划分为一个个小的子空间，位于每一个子空间内的样本都有唯一确定的类别。

3.1、k值的选择

对于k值得选择，不同得k值会对k近邻法得结果产生显著得影响，这里直接引用《统计学习方法》这本书上得一段话：

a、如果选择较小的k值，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差( approximation error)会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用。但缺点是“学习”的估计误差(estimation error)会增大，预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。换句话说，k值的减小就意味着整体模型变得复杂，容易发生过拟合。
b、如果选择较大的k值，就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误。k值的增大就意味着整体的模型变得简单。
c、如果k=N,那么无论输入实例是什么，都将简单地预测它属于在训练实例中最
多的类。这时，模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的

上面得近似误差可以近似理解为算法对于训练样本的预测能力也就是训练误差，估计误差可以理解为算法对于测试样本的预测能力也就是测试误差。

3.2、相似性评价策略

相似性评价策略是基于两个样本特征空间的取值来判断两个样本间的相似性程度，具体到k近邻算法中也就是待分类样本与已标记样本间的相似性程度，从而选取与待分类样本最相似的k个样本。
评价两个样本间相似性程度的指标往往不止一个，但最简单最直观的就是两个样本间的距离，但同样两个样本点间的距离也不止一种甚至可以认为有无穷多种距离，最常见的有曼哈顿距离、欧氏距离，或更一般的Lp距离，Lp距离的计算公式如下：
$$L_p(x_i,x_j)=(\sum _{i=1}^n|x_i^{(l)}-x_j^{(l)}|p{)}^{\frac{1}{p}}$$
上式中当p取值为1时Lp距离就是曼哈顿距离，Lp取值为2时Lp距离就是欧式距离，当p取值为无穷大时，Lp距离就是两个样本点间各个维度距离的最大值，即：
$$L_{\infty }(x_i,x_j)=max|x_i^{(l)}-x_j^{(l)}|$$
显然，按照我们的常识，在大多数情况下距离越近的两个样本越相似，因此在算法实现中我们只需要按照事先确定好的距离计算规则计算待分类样本点与每一个已标记样本间的距离，然后进行排序得到距离最近的k个已标记样本点即可。

PS：由于我专业学的测绘地理相关的，因此可能对距离之类的概念更敏感，实时上有些时候并不是距离越近的两个个体相似性程度越高，尤其是当距离为空间距离时，这种情况更加普遍，距离越近的两个个体差异可能会更大，这种现象称为空间负相关，最常见的例子就是大城市对周围小城市的虹吸效应，如北京，越靠近北京的城市受北京虹吸效应的影响越越大，人口、资源流失越严重，经济反而会越差。当然也有空间正相关的例子，比如大城市对周围小城市的溢出带动效应，如上海，越靠近上海的城市受上海溢出带动影响越明显，经济发达。不过这些都是后话，在绝大多数的应用场景中认为越接近的两个样本属性越相似时没有问题的

3.3、分类决策规则

分类决策规则就是指在依据选取的k值和相似性评价策略从已标记样本中选出k个与待分类样本最相似的样本后，如何基于这k个样本确定待分类样本类别的问题。
最常用的分类决策规则就是投票策略，即统计归并k个样本的类别，哪一个类别对应的样本数最多，待分类样本就属于哪一个类别，简单将就是少数服从多数，从概率统计的角度来讲投票策略等价于经验风险最小。
当属于两个类别如A类和B类的样本数一样多时，这时候可以附加考虑待分类样本到A类样本点和B类样本点的平均距离，哪一个平均距离小就属于哪一个类别。更进一步，事实上，我们可以在一开始就同时考虑待分类样本到各类样本点的平均距离和各类样本点的数目，给平均距离和样本数分别赋予不同的权重，计算加权分数再进行归算比较，得分最高的类别就是待分类样本点最终所属的类别。

4、算法实现——kd树

上面所过，k近邻算法没有一个显示的学习过程，对每一输入的待分类样本点都要依据实现确定好的k值和相似性评价策略选出与待分类样本最近的k个已标记样本，再依据分类决策规则确定待分类样本点的类别，每一个输入的待分类样本都k个不同的最近样本点，因此实现k近邻算法的难点在于如何快速找的与待分类样本最近的k个样本点。

---

最简单直观就是线性扫描：依据相似性评价策略（这里以距离为例）计算待分类样本与每一个已标记样本点的距离，依据距离对待分类样本点进行排序，基于排序的结果找出k个最近的已标记样本点进行分类。线性扫描的算法复杂度为O(n²)，当样本数很多，特征空间的维数较多时，线性扫描算法就会非常耗时，难以满足实际生产的需要。因此需要一种特殊的数据结构存储训练数据，以减少计算距离的次数，提高算法运行的效率，kd树就能够满足上述要求。(kd树中的k和k近邻算法中的k没有特定的联系，请不要做过多的联想哈！)

---

4.1、kd树生成

kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，kd树是二叉树，表示对k维空间的一个划分，kd树生成方法如下：

• 构造初始超矩形区域，使该超矩形区域对应于k维空间中的所有已标记样本点。这里的超矩形区域可以看作维度数为k的矩形，当k=2时就是平面二维矩形，当k=3时就是三维立方体，当然k也可以为4，5，……n，这里的k就是样本点的特征数
• 按照如下的方法进行递归，不断的对k维空间进行切分，生成子节点：在超矩形区域上选择一个坐标轴（一个维度）和在此坐标轴上的一个切分点（该维度的一个取值），确定一个超平面，这个超平面通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域，此时所有的已标记样本点（除切分点）被分到这两个子区域中。对这两个子区域重复上述操作（递归），直到子区域内没有实例点为止。在这个过程中实例被保存到相应的切分点中
• 通常依次从k个维度中选择一个维度对空间进行切分，选择的切分点为子超矩形区域中的已标记样本点在该维度上的中位数为切分点。此时得到的kd树为二叉平衡树，二叉平衡树的搜索效率不一定是最优的。关于二叉树和二叉平衡树感兴趣的可以参考这篇博客，不了解也没关系，不影响对k近邻算法的理解

下面以一个例子来演示kd树的生成过程：
有如下二维数据集：{（2，3），（5，4），（9，6），（4，7），（8，1），（7，2）}，按图1、2、3、4所示的步骤生成kd树

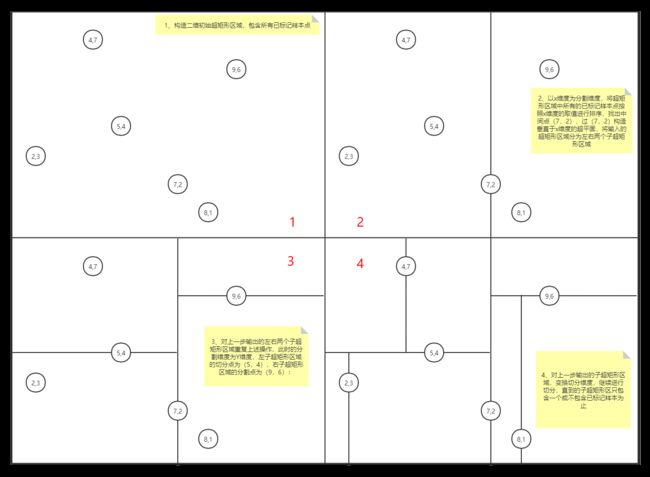
最终得到的kd树如下图所示：

4.2、kd树搜索

kd树搜索就是指对一个输入的待分类样本点，从由已标记的样本点构成的kd树中找出k个与待分类样本点最近的样本。不同于线性扫描，基于kd树能够省去对大部分已标记样本点的搜索，提高搜索效率，其算法复杂度为O(logN)，N为已标记样本点的个数。

接下来结合上图对kd树搜索步骤进行说明：

1. 从kd树的根节点向下遍历，找到包含待分类样本点(2,5)叶子节点(4,7)，该叶子节点对应于包含该待分类样本点的最小超矩形区域。遍历方式：若kd树节点的切分维度纬度值小于输入的待分类样本点的切分维度维度值则从该节点的右子树向下遍历，否则从该节点的左子树向下遍历，直到到达叶子节点,如节点（7，2）的切分维度为x维度，7>2，从（7，2）的左子树向下遍历，（5，4）的切分维度为y维度4<5，因此从（5，4）的右子树（4，7）开始遍历，（4，7）为叶子节点停止遍历。
2. 以叶子节点(4,7)为距离待分类样本最近的当前最近点，以待分类样本(2,5)为球心，待分类样本到当前最近点的距离为半径，组成一个超球(图中绿色的圆)，距离该待分类节点的最近点一定在该超球体内部。在二维空间中超球对应于平面上的一个圆，在三维空间中超球对应于空间中的一个球体。
3. 从当前最近点的父节点（5，4）开始向上遍历，进行如下判断：
   3.1. 计算该父节点（5，4）到待分类节点的距离，判断该父节点是否在超球体的内部，若在超球体的内部，从该父节点为新的当前最近点，回到步骤3重新向上遍历
   3.2. 若该父节点不在超球体内部，则判断该父节点的另一子节点（2，3）对应的超矩形区域与超球体是否相交。若相交，则以该节点(2,3)为根节点的子树中可能存在新的当前最近点，需要遍历该子树中的每一个节点并判断节点是否在超球体内部，若在超球体内部就是新的当前最近点，此时回到步骤3，从新的当前最近点的父节点开始向上遍历；若不相交，则继续从父节点的父节点开始向上递归，直到到达根节点，此时的当前最近点就是与待分类样本点最近的点。

补充：

1. 如何判断超球体与子超矩形区域是否相交：计算待分类样本点的切分维度纬度值与父节点的切分维度纬度值之差的绝对值，该值对应于待分类样本点到该子超矩形区域的距离(图中黄色虚线部分)，若该距离小于超球体的半径则相交，否则不相交
2. 上面的步骤论述了如何从kd树中搜索出距离待分类样本点最近的一个已标记样本点，如果要搜索k个最近已标记样本点只需要将上述步骤重复k次即可。

5、代码编写

下面对代码实现k近邻算法中的一些关键步骤进行说明

5.1、快速排序

在生成kd树的过程中，需要按照已标记样本点切分维度的维度值进行排序，找出中间的点作为切分点。为了提高算法效率可以选用更高效的排序算法，相较于一般的冒泡排序和选择排序，这两者的算法复杂度为O(n²)，快速排序的算法复杂度为O(N·logN)。感兴趣的可以参考这篇博客，对快速排序算法思想的讲解很通俗易懂，但采用冒泡排序和选择排序也没有问题，毕竟kd树的生成操作只会执一次，不会对算法效率产生很大影响

5.2、二叉树遍历

当父节点的另一子节点对应的超矩形区域与该超球体相交时需要遍历以该子节点为根节点的子树，二叉树的遍历可以参考这篇博客

5.3、代码逻辑

kd树节点的存储结构：

def __init__(self,xdata,ydata,field):
        #已标记样本点的各个维度取值，用于计算已标记样本点与待分类样本点的距离
        self.xdata=xdata
        #已标记样本点的标记(类别)
        self.ydata=ydata
        #已标记样本点的切分维度，用于向下遍历二叉树和判断该节点对应的超矩形区域与待分类样本点的超球体是否相交
        self.field=field
        #该节点的父节点，用于向上遍历二叉树，寻找与待分类样本点最近的已标记样本点
        self.father=None
        #该节点的左、右子树，用于向下遍历二叉树以及最近点的搜索
        self.left=None
        self.right=None

5.3.1、kd树生成

kd树生成比较简单，感兴趣的可以直接看代码(实际情况是我实在写不下去了，最近事情实在太多了，一篇博客断断续续写了几天，太难了)

5.3.2、kd树搜索

向下遍历kd树搜索包含分类节点的叶子节点：

向上遍历搜索与待分类节点最近的节点：

5.4、结果展示

用于算法验证数据集为机器学习中常用的鸢尾花数据集，该数据集共有150个样本，每个样本有4个特征（维度），分别是花瓣长度、花瓣宽度、花萼长度、花萼宽度。
采用的算法验证方法为交叉验证，将鸢尾花数据集分为了10份，取出一份(15个样本)用来做测试集，其余9份（135个样本）做训练集，循环10次，这样每一份样本都能够做测试集参与测试，输出每一次算法验证的结果，主要从准确率和召回率两个方面进行评价。
为了使结果看起来更加直观，代码中带用了matplotlib对训练数据和测试数据进行了可视化处理。由于鸢尾花数据集有四个维度，无法选取所有的维度进行可视化，所以为了尽量减少信息损失，使可视化的效果更好，先用PCA主成分分析对数据进行了降维处理，取前两个主要维度进行可视化(当然在这里PCA不是我们的主题，所以为了方便，直接选两个维度进行可视化也可以，但效果可能会差一点)。
最终结果如下图所示：点状符号为训练数据，三角符号为测试数据，同一颜色代表同一类别，图中显示的是测试数据的预测类别

6、代码获取

百度云：https://pan.baidu.com/s/1tmXtB8oG4oTgryPyNu8vGg提取码：650y
CSDN：https://download.csdn.net/download/TJLCY/18169704

结语

---

虽然这学期毕业设计很忙，但还是想自学一些算法，毕竟像一些回归、分类、聚类算法，在遥感领域中的应用还是挺多的。虽然，之前也了解过感知机、PCA，Kmean等算法，但都是学了，用了，过后一段时间后就忘了，所以感觉还是有必要好好做一个学习记录，所以就写了这篇博客，后面争取继续写下去。加油吧，骚年！

---