文章目录
-
-
- 代码解析
-
- 1. 载入数据, 归一化
- 2. 设置一些参数
- 3. 参数变换带来的影响
-
- scale参数的变化影响
- angle参数变化影响
- 投影变换下eye位置的影响
代码解析
1. 载入数据, 归一化
C = sio.loadmat('Data/example1.mat')
colors = C['colors']
colors = colors / np.max(colors)
vertices = vertices - np.mean(vertices, 0)[np.newaxis, :]
2. 设置一些参数
'''
现实中一般脸是18cm长宽, 这里设置180=18cm, 图片尺寸256×256
'''
face in reality: ~18cm height/width. set 180 = 18cm. image size: 256 x 256
scale_init = 180 / (np.max(vertices[:, 1]) - np.min(vertices[:, 1]))
camera['proj_type'] = 'orthographic'
3. 参数变换带来的影响
scale参数的变化影响
for factor in np.arange(0.5, 1.2, 0.1):
obj['s'] = scale_init * factor
image = transform_test(vertices, obj, camera)
- 示例图:

angle参数变化影响
for i in range(3):
for angle in np.arange(-50, 51, 10):
obj['angles'][i] = angle
image = transform_test(vertices, obj, camera)

-
绕y旋转
-
绕z旋转

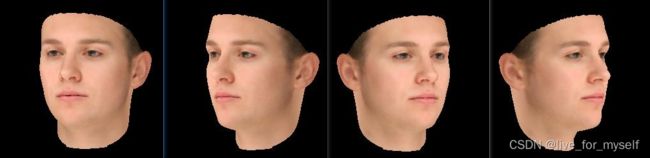
投影变换下eye位置的影响
camera['proj_type'] = 'perspective'
camera['at'] = [0, 0, 0]
camera['near'] = 1000
camera['far'] = -100
camera['fovy'] = 30
camera['up'] = [0, 1, 0]
for p in np.arange(500, 250 - 1, -40):
camera['eye'] = [0, 0, p]
image = transform_test(vertices, obj, camera)
def transform_test(vertices, obj, camera, h=256, w=256):
'''
根据矩阵做3d点欧式变换
'''
R = mesh.transform.angle2matrix(obj['angles'])
transformed_vertices = mesh.transform.similarity_transform(vertices, obj['s'], R, obj['t'])
if camera['proj_type'] == 'orthographic':
projected_vertices = transformed_vertices
image_vertices = mesh.transform.to_image(projected_vertices, h, w)
else:
'''
在从世界坐标系到相机坐标系的变换中, 这里只是因为eye方向的不同, 所以实质上只是变换了
'''
camera_vertices = mesh.transform.lookat_camera(transformed_vertices, camera['eye'], camera['at'], camera['up'])
projected_vertices = mesh.transform.perspective_project(camera_vertices, camera['fovy'], near=camera['near'],
far=camera['far'])
image_vertices = mesh.transform.to_image(projected_vertices, h, w, True)
rendering = mesh.render.render_colors(image_vertices, triangles, colors, h, w)
rendering = np.minimum((np.maximum(rendering, 0)), 1)
return rendering
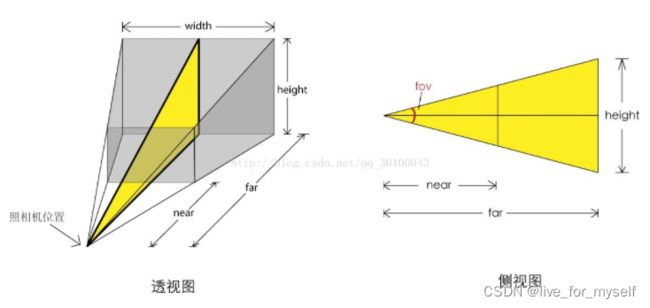
- 下面是投影变换, 使用了从视锥到正方体的变换, 但是这里好像并没有视口变换
参见透视投影原理介绍

def perspective_project(vertices, fovy, aspect_ratio = 1., near = 0.1, far = 1000.):
''' perspective projection.
Args:
vertices: [nver, 3]
fovy: vertical angular field of view. degree.
aspect_ratio : width / height of field of view
near : depth of near clipping plane
far : depth of far clipping plane
Returns:
projected_vertices: [nver, 3]
'''
fovy = np.deg2rad(fovy)
top = near*np.tan(fovy)
bottom = -top
right = top*aspect_ratio
left = -right
P = np.array([[near/right, 0, 0, 0],
[0, near/top, 0, 0],
[0, 0, -(far+near)/(far-near), -2*far*near/(far-near)],
[0, 0, -1, 0]])
vertices_homo = np.hstack((vertices, np.ones((vertices.shape[0], 1))))
projected_vertices = vertices_homo.dot(P.T)
projected_vertices = projected_vertices/projected_vertices[:,3:]
projected_vertices = projected_vertices[:,:3]
'''
y 反向
'''
projected_vertices[:,2] = -projected_vertices[:,2]
return projected_vertices




