Depth from Motion:探索突破纯视觉 3D 检测瓶颈
本文作者:
@王泰
1 前言
当我们说单张图像估计深度本身是一件“不靠谱”的事情时,什么是“靠谱”的呢?
为什么单张图像估计“不靠谱”,多张图像就“靠谱”了呢?
而什么样的多张图像又会更“靠谱”一点呢?
这篇文章将在纯视觉 3D 检测的任务语境下,针对自运动估计深度这一问题展开介绍,阐释利用多视角几何估计深度的合理性和有效性,讨论这一支持性原理为之后纯视觉 3D 感知提供的全新可能性。
本文基于我们最近被 ECCV 2022 接收为 oral 的论文:Monocular 3D Object Detection with Depth from Motion (DfM),但会更侧重于讲解研究动机和主要结论,希望能借此引发社区对于多视角估计深度这一机遇更多的思考和尝试。
论文链接:Monocular 3D Object Detection with Depth from Motion
目录
本文作者:
1 前言
2 问题回顾
2.1 任务定义
2.2 定位瓶颈
2.3 近期趋势
3 “像人一样”感知三维世界
3.1 从直觉出发
3.2 理论分析
3.3 结论
3.4 讨论:视频中的 2D vs 3D 目标检测
4 利用时序多视角几何估计深度和检测 3D 物体
4.1 框架总览和损失度量的构建
4.2 单目理解的补偿
4.3 Pose-Free Depth from Motion
5 实验结果
5.1 定量结果
5.2 定性结果
5.3 消融实验
6 从深度估计视角重新审视 BEV 感知潮流
7 讨论
2 问题回顾
在开始这篇文章的讲解之前,首先让我们回顾下任务定义,以及之前的研究有哪些重要结论。
2.1 任务定义
我们要解决的问题是要通过纯视觉输入,即单视角或多视角图像,检测出图中感兴趣的物体并估计出他们的 3D 框。
在驾驶场景中,3D 框通常的表示方式包含 7 个自由度,其中包含 3 个自由度描述物体中心的 3D 位置,3 个自由度描述物体的大小,以及 1 个自由度描述物体在地面上的转向角(图 1)。
图 1:单目 3D 检测设定在给定一张或多张二维图像下,检测出物体的类别和 3D 框,其中 3D 框通常拥有至少 7 个自由度:三维位置,三维框大小以及转向角
在解这个问题时,一年前大家端到端的做法通常集中在直接从 perspective view,即透视视角/图像视角,来估计 3D 框经过拆解后的多个回归量:物体中心在图像上的投影、深度、框的大小和转向角。
这一方案的优点在于可以非常自然地从 2D 检测过渡到 3D 任务,从结构上讲和 2D 检测差别不大,因此可以利用诸多 2D 检测中的经验,并构建两个任务之间的联系。但由于回归目标从原来全部都是存在于二维图像上的估计量(2D 框)扩展到需要估计三维空间的度量(深度,3D 框大小),无论从原理上还是效果上都显然不是最优解。
图 2:不准确的深度阻碍了其他所有预测目标对于总体 3D 检测性能的提升。
2.2 定位瓶颈
接着,后续工作(MonoDLE [1], 3D-Conf [2], PGD [3])找到了这个问题中的性能瓶颈:物体的深度估计不准确(图 2)。后面也有很多工作 [1,2,3,4,5] 尝试从概率、几何等各个角度来更好地解这个问题。
但这些方法都还是基于单张图片来估计深度,从原理上讲还是没有解决根本问题:单张图像我们最多只能估计物体的相对深度,而其对于绝对深度的估计在某种程度上十分依赖训练数据集和测试数据集在相机内参、数据分布等多方面的一致,因而具有较差的泛化性和稳定性。
更多细节可以参考我们之前这篇文章来回顾。
2.3 近期趋势
与此同时,随着 Tesla 公开其感知部分的技术方案,加上学术界有 nuScenes 这样一个有环视相机设置的数据集开始被大家所关注,一股基于 BEV(鸟瞰图)的潮流突然兴起:CaDDN [6],DETR3D [7],BEVDet [8],BEVFormer [9] 等。这些工作从很多方面延续了之前 Pseudo-LiDAR [10] 和 OFTNet [11] 的一些初步想法,随着单目 3D 基线算法和(LiDAR-based 方法中)基于 BEV 的检测头逐渐成熟,这类方法在最近终于开花结果。
这类方法一个最直观的优势在于:不需要再通过复杂的后处理操作(如 nms) 来融合每个视角的检测结果,就可以直接输出整个环视视角下的 3D 检测结果。另一个“看起来”的优势在于:通过转换特征到 BEV 下检测物体而间接避免了直接的深度估计。
在这两点分析中,前者是显而易见的,而后者只是表面现象,其实暗藏玄机。接下来,我们就将通过一系列分析阐述如何在更好的深度估计层面寻求纯视觉 3D 检测的突破口,以及从深度估计角度再来审视 BEV 方法的成功。
3 “像人一样”感知三维世界
3.1 从直觉出发
既然我们知道单张图像很难直接估计物体的绝对深度,那该如何解决这一问题呢?众所周知,人对于三维场景精细的感知离不开两只眼睛,如果要完成物理上相对精确的测距还是需要这样一套双目的设定才可以满足几何上的合理性。
除了单目和双目之外,另外一个会在不自觉中采用的感知逻辑是通过自身运动估计物体深度:可以想象,当我们开车时,通常来讲我们看到的“移动快”的区域一般是近的,而“移动慢”的是远处。事实上,通过自身运动估计物体深度的原理是和双目类似的,大家都是在不自觉中通过观察(匹配)空间中同一个点在不同视角中的不同位置,来根据事先知晓的两个视角间的的距离关系“计算”出物体的深度信息。
3.2 理论分析
以上是我们的直觉,其实并没有涉及到具体定量的计算,因而我们还是停留在定性分析层面:只是能知道通过这三种逻辑我们可以估计物体的“远近”,而并不清楚如何具体估计这个物体“有多远”。
前面说到,通过单目图像,我们从定量计算角度一般只能根据图像中一些先验信息,例如物体的排列、大小、地平线等大致知道物体的相对深度;而对于后两种基于多张图和匹配来进行深度估计的方法,又存在怎样的几何原理支撑呢?我们在文章的理论分析部分对于这两类情况进行了直接的比较。
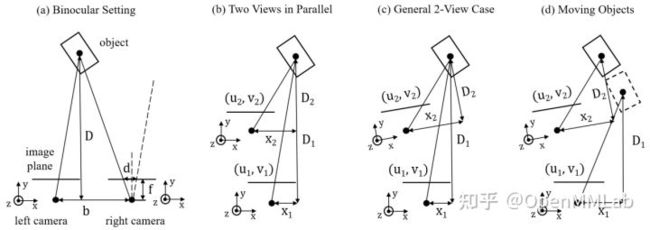
图 3:用于估计物体深度的在不同情形下的多视角几何:(a) 双目,(b) 平行的两个视角,(c) 通常的任意两个视角,(d) 目标物体正在运动。
首先对于双目的情况,如图 3-(a) 所示,两个相机处在同一个平面上,只有水平方向的固定位移 b,我们通常称之为基线(baseline)。假设物体的深度是 D,相机焦距为 f,物体中心在两个相机上投影点的距离 d(视差 disparity),通过一个大家熟知的相似三角形关系,我们可以得到物体的深度:
df=bD⇒D=fbd (1)
在这个关系式中,f 和 b 都是事先知道的常量,因此我们可以将深度估计问题直接转化为视差估计问题,而视差估计问题其实是视觉研究中一种典型的匹配问题,这也是之前双目方法大多会依赖的一个基本思想。
接着,当我们把这一多视角设置扩展到平行的两个视角,如图 3-(b) 所示,我们是否还可以得到如此简洁直接的几何关系呢?假设物体在两张图上的投影点分别为 (u1,v1) 和 (u2,v2) ,物体在两个视角下的深度分别为 D1 和 D2 ,在如图定义的坐标系下 x 方向的坐标为 x1 和 x2 ,相机内参矩阵为:
P=(f0cu0fcv001)
其中 cu 和 cv 为相机中心在图像中的位置(以像素 pixel 为单位)。则我们可以得到如下关系:
u1−cuf=x1D1,u2−cuf=x2D2,Δx=x1−x2,ΔD=D1−D2 (2)
其中 Δx 和 ΔD 即为物体自运动在两个方向上的分量,进而我们可以得到 D1 的表达式:
D1=f(Δx−u2−cufΔD)u1−u2=ΔD=0fΔxu1−u2 (3)
如表达式中所述,当 ΔD=0 时,这一关系式会退化为双目的情形。而在通常情况下,不同于双目系统,这一情形形成的基线 Δx−u2−cufΔD 是一个动态的,它依赖于自身运动产生的 Δx 和 ΔD 以及物体在图像上投影在水平方向的绝对位置 u2 。相应的,物体深度估计不再只依赖于视差估计。
为了更好地理解这一情况,我们可以以 KITTI 中的双目系统为例来做一个定量分析。大家知道一个合适的基线是深度估计的基础,这个基线不能过大或过小。过大的基线会导致图像之间 overlap 太小,过小的基线会导致视差太小从而使估计误差变大。
我们以 KITTI 的双目系统基线为参考(0.54 米),看下如何通过 (3) 式中的自身运动来实现这一基线。考虑车自身只向前运动的情况,即 Δx 远小于 0.54 米,那么我们需要一个相对较大的深度方向的位移 ΔD 以及一个相对较大的 u2−cu 来构造基线。比如要实现 0.54 米的基线, ΔD 有 5.4 米,焦距为 700 pixels,那么 u2−cu 需要大概 70 pixels 来实现这一基线;相应的,如果 ΔD 只有 2.7 米,那么我们需要 u2−cu 大概 140 pixels 来实现这一基线(作为参考,KITTI 中一张图的一半长度为 600 pixels)。这意味着,我们在对于远离图像中线的物体进行深度估计时可以相对准确,而会在估计中线附近的物体时遇到麻烦。
在此基础上,引入更复杂的自运动,如图 3-(c) 中的旋转,会在 (3) 式的分母中引入旋转的系数;而引入目标物体的运动,如图 3-(d) 所示,会在 (3) 式中引入物体运动的估计。因此,更多有关物体绝对位置以及其运动估计的量的引入使得直接通过视差估计来预测深度存在根本上的困难。(更多分析细节见文章的补充材料)
3.3 结论
根据以上分析,我们观察到在一个通常的多视角系统中估计深度有两方面问题:
- 由于物体绝对位置、物体运动等多个额外估计量的引入导致不可避免的累积误差,直接通过视差估计来估计物体深度存在根本上的困难;
- 基于时序多视角匹配的方法存在一些无法从根本上估计深度的情况:如自身静止而没有形成基线,以及在纹理比较少的区域存在匹配模糊性的问题。
于是,在第四节中我们将展示:受最近双目 3D 检测方法的启发,我们采用了一个 geometric cost volume(几何损失度量)的方法来作为一种变通的方式来引入帧间几何关系从而避免第一个问题;同时通过增加一路单目理解的分支,以及一个简单可解释融合机制来初步解决第二个问题。
3.4 讨论:视频中的 2D vs 3D 目标检测
在接下来讨论视频中的 3D 目标检测之前,除了双目系统在这里有一定借鉴意义之外,另外一个相关问题是“视频中的 2D 目标检测”。受益于 OpenMMLab 全家桶,我们在项目初期也非常方便地尝试了一些 2D 视频目标检测的方案,如 DFF [12] 和 FGFA [13],然而效果却并不理想。
经过简单分析,我们可以理解的是视频中的 2D 目标检测和 3D 目标检测利用时序信息解决的是完全不同的问题。在 2D 情形下,视频数据通常为一个固定的或者有很小唯一的相机采集的,物体本身不是刚体,并且会快速移动。
在这种情况下,通过聚合多帧特征来更好地处理物体在运动过程中被遮挡或模糊的情况是可以得到更准确的 2D 框的。相比在我们目前的 3D 情形中,目标大多不会有很大形变,遮挡问题也不是主要瓶颈,通过连续帧关联增强结果稳定性也不会从单帧检测精度上有过多提升,更重要的还是通过以上叙述的几何关系来估计深度才能从根本上提升检测性能,当然还有一个副产物是可以估计速度。这种对于 2D 和 3D 类似任务不同视角的分析在当前打通两个领域之间联系尤为重要。
4 利用时序多视角几何估计深度和检测 3D 物体
图 4:DfM 框架的总览图
4.1 框架总览和损失度量的构建
上面提到,在观察到直接通过估计视差来估计深度存在根本困难之后,我们从最近的双目 3D 检测方法中获得启发,采用了类似 DSGN [14],LIGA-Stereo [15] 的几何损失度量 (geometric cost volume) 来引入不同视角的几何关联,只是之前双目的两个视角在这里变成了时序上的两帧。
同时,由于损失度量构造本身涉及到的基于相机位姿的 warping 比之前双目更加复杂,我们通过 grid sampling 等方式也重新实现了一套构造方式,并且保证这一 warping 始终在真实世界坐标系下完成,从而能够对各种对于输入图像的数据增强兼容,如图 5-(a) 所示。
具体来说,整体的网络结构可以分为三部分(如图 4):第一部分是对于输入的两帧图用常规的 2D 骨架网络提取 2D 特征,第二部分是基于两个 2D 特征构造 cost volume 并实现向 3D 特征图的转换,第三部分则是基于 3D 特征图接上 3D 检测骨架和检测头实现 3D 目标检测。
其中相对复杂的部分在于,在给定 2D 特征图后如何构造 3D 特征图:这里需要提前预设一系列深度的采样点,比如每 0.2 米一个采样点,从 2 米到 59.6 米放置 288 个采样点,来将 2D 特征图复制 288 份得到单帧图的 cost volume;之后通过坐标变换将两帧的 cost volume 对齐到同一个坐标系下,再通过一系列 3D 卷积最终用来预测深度的分布。
注意这里所做的事情其实就是在利用 stereo correspondence 预测每个点的深度,只有当两个 cost volume 在同一个位置的特征相似度更高时,才能说明这个点是在两张图上真实看到的、有对应关系的点。
这一包含有 stereo correspondence 和深度预测信息的 volumetric feature 在深度图的监督下包含了更多的几何信息,加上原本 2D 提取的语义信息,从而共同为后续的 3D 检测服务。限于篇幅,这里对于具体实现不再做更多赘述,更多细节可见论文和代码。
图 5:(a) 多视角损失度量的构建和 (b) 单目理解的补偿。
4.2 单目理解的补偿
单目和多视角估计深度从原理上存在本质的差异:单目估计依赖对于单张图中语义和几何的理解,以及数据驱动的先验(如物体类别、大小、类似外观的物体的绝对深度);而多视角估计的方法依赖基于外观特征的匹配准确度。
如之前理论分析中提到,有一些深度估计情形本身是基于时序多视角匹配难以处理的,例如静止相机不能形成基线、目标在运动无法进行匹配以及少纹理的区域。因此,我们在原本多视角构造立体特征图的基础上,增加了单目理解的一条分支,并且在图中不同位置实现了简单而有效的自适应性融合。
简单来说,在得到两帧图的 cost volume 之后,一条分支构造了多视角的 cost volume 并提取立体特征,另一条分支保持单张图的 cost volume 并用类似的网络提取单目理解的特征。在最后融合时,我们通过一个简单的 1x1 卷积将两个 cost volume (特征维 C x 深度维 D x 图像维 H x W) 在 C x D 维度上进行融合,得到 D x H x W 的权重用来融合两个 volume,如图 5-(b) 所示。
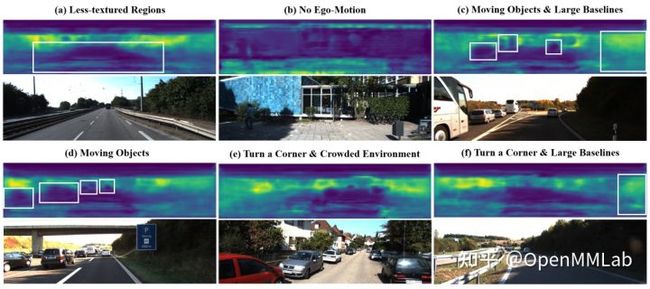
直觉上理解,这意味着每个点在融合两种估计时考虑了其在图像对应位置上所得到的深度估计分布,根据其置信度在图像的不同位置上自适应融合。受益于这种可解释性的融合方式,我们也可视化出相应的权重图来印证我们的理论分析。如图 6 所示,我们将权重在图像中不同位置的数值通过热度图的方式可视化出来,越亮的地方说明越依赖多视角几何,越暗的地方说明依赖单目更多一些。
图 6:融合权重在不同情形下的可视化。
可以看到,在 (a) 少纹理 (b) 没有自运动 (c) 运动物体这些情况下显然都是依赖单目估计深度更多一些,而在纹理类似的情况下,离图像中线越远的区域 (c & f) 越依赖多视角几何估计。同时由于我们上述分析是基于没有自运动旋转的情况下,而当自车在进行转向的时候,由于转向角短时间不会很大,可以看到分析依然基本成立 (e)。
4.3 Pose-Free Depth from Motion
至此我们拥有了一个完整的框架可以从连续帧图像中估计深度和检测 3D 物体。其中,自运动在里面作为很重要的一个线索,像双目系统中的基线一样,来帮助我们可以实现 metric-aware 的绝对深度估计。尽管自运动在实际应用中并不难获得,我们在这里依然提出了一种不需要自身姿态变换的解决方案,这对于这套方案应用的灵活性非常重要。
自身姿态变换估计的重点主要在于回归目标的建模方式。自身姿态变换作为一种刚体变换,通常可以分解为一个三个自由度的平移量 t 估计,和一个三个自由度的旋转估计。
其中在表达旋转时最常用的方式是用三个欧拉角,但这种周期性的回归目标在实际实验中通常表现得不太稳定,同时会有潜在的万向锁问题(虽然在驾驶场景通常不会有)。于是我们采用了单位四元数(unit quaternion)的表达方法来避免这些问题。我们的基础方案直接采用自身姿态的标注作为真值,用 L1 loss 来进行监督:
Lt=||t−t^||1,Lr=||q−q^||q^||||1,Lpose=Lt+λrLr. (4)
其中我们将输出的四元数预测 q^ 归一化来作为旋转的估计,用 λr 来调整平移和旋转损失函数的比重。这一方式有明显的几个问题:
- 调整λr本身是一个困难并且高成本的事情;
- 直接从 2D 图像估计 3D 自运动又是一个有 domain gap 的问题;
- 在训练时我们仍然需要姿态的真值。
为了解决这些问题,我们使用了一种自监督重投影的方式来代替这种监督方式。具体来说,我们根据当前帧的深度估计,用估计的自身姿态变化重投影之前帧图像 It−δt 来得到当前帧图像 It−δt→t ,并和真实的当前帧图像 It 计算 photometric loss(图 4)。加上一个 depth smoothness loss Ls 构成 pose 估计的 loss:
Lpose(It,It−δt)=Lp(It,It−δt→t)+λsLs (5)
类似的 loss 曾在基于视频的自监督深度估计工作 [16,17] 中被使用,需要注意的是,和那些工作联合优化深度和相机位姿不同,我们有深度的真值图来监督深度的学习,而只用这个 loss 来监督相机位姿的学习。通过这种方式,因为有绝对深度的真值监督,我们可以在没有相机姿态真值的情况下学习到 metric-aware 的 ego-pose。
5 实验结果
5.1 定量结果
我们的方法在 KITTI [18] 上进行了验证,如表 1 所示,我们的方法不论有没有使用 pose 都比之前方法明显表现要好,在 3D 和 BEV 上的 AP 分别能高出 2.6%~5.6% 和 4.2%~7.5%。同时也比之前最好的基于 video 的单目 3D 检测方法 Kinematic3D [19] 表现更好。
值得注意的是,我们的方法和 Kinematic3D 增强检测稳定性的方法并不矛盾,未来也可以尝试将两者结合起来得到稳定准确的检测结果。
另一方面,和双目方法相比(LIGA-Stereo 在 moderate 上可以达到 64.7% AP),我们依然还有很大的空间可以挖掘。这可能和 depth from motion 内在的一些问题有关,但也依然值得在这方面进一步探索,毕竟双目的方法从早期的 RT3DStereo [20](23.3% AP)到现在也是提升了 40% AP。
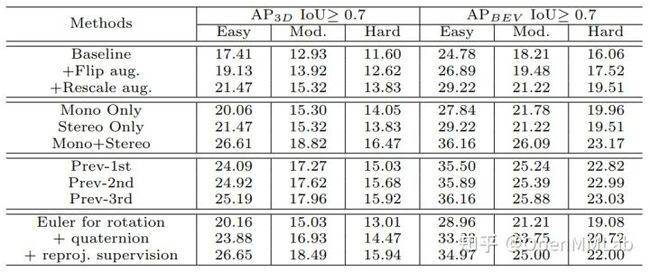
表 1:KITTI 验证集上的 3D 检测性能对比(AP40)。5.2 定性结果
5.2 定性结果
除了之前提到的对于融合部分 weight map 的可视化和可解释性分析外,我们也画出了检测结果以及深度估计结果的各种视角图来展示方法的大概效果:
图 7:检测结果在透视/图像视角的可视化效果。
图 8:深度估计结果投影到 3D 空间中,以及检测结果在 3D 视角下的可视化效果。
5.3 消融实验
表 2:消融实验,从上到下分别为:(a) geometry-aware 损失度量的构建,(b) 不同深度估计方法的检测性能,(c) inference 时采用不同的之前帧,(d) 不同的 pose-free 设计。
在消融实验中,我们展示了一些针对模型中重要设计的实验结果。从表 2 中可以看到,geometry-aware 损失度量的构建、单目估计的补偿以及 pose-free 的几点设计都起到了重要作用。
另外,我们也测试了 inference 时使用哪一帧去构造 cost volume 对于性能的影响,可以看到如我们所预期,用到最前面一帧的时候会相对表现更好一些,因为可以通过更大的 ego-motion 实现更合适的等价基线。
由于 KITTI 上的连续帧设定有些限制,在这一方面其实也存在一定的探索空间,例如在 nuScenes 和 Waymo 上,在拥有更多之前帧的时候,如何选取之前帧用于训练和测试也值得进一步试验。
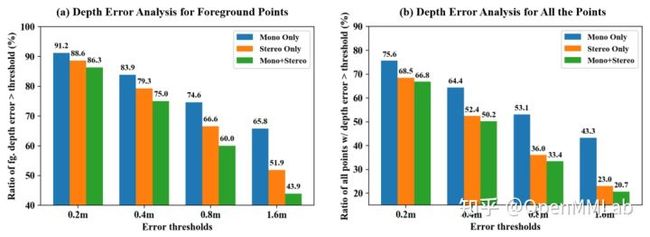
图 9:我们通过分别比较误差超过阈值 0.2m、0.4m、0.8m 和 1.6m 的点的比例,在前景和全图区域上对于不同方法的深度预测进行了误差分析。单目/多视角/融合的方法在前景和全图上的误差中位数分别为5.86/3.33/2.60m 和 1.15/0.58/0.48m。
最后,除了检测性能的提升外,更直接的测试方法是对于我们深度估计部分的性能进行测试。如图 9 所示,我们针对有 LiDAR 投影点/深度真值的地方计算了深度估计的准确性,可以看到不管在前景还是全图范围内,深度估计的准确度都有一个显著提升。特别是全图范围内,在背景的深度估计占据很大比例时,基于时序多视角的深度估计方案不会受到移动物体很大影响,因而效果提升比前景较为明显。基于同样道理,前景的深度估计上,由于对于运动物体的处理更加完备,从单纯基于多视角的估计方案到加入了单目补偿也获得了较大性能提升。
6 从深度估计视角重新审视 BEV 感知潮流
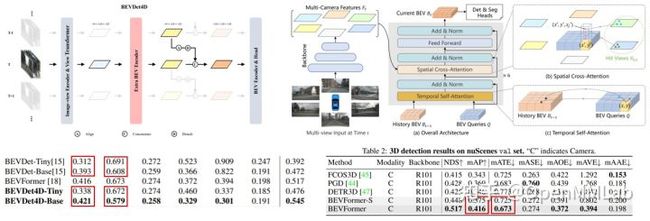
图 10:近期一些基于多视角和 BEV 的工作在引入时序信息时其实也已经隐式地引入了立体匹配的思想,并从中获得了显著提升。
在介绍完我们的分析和方法之后,相信大家对于纯视觉各种 setting 如何来实现 3D 感知的原理有了更深刻的理解。基于此,我们再来回顾开篇时提到的问题,BEV 之所以如此简洁而有效的原因在哪里:其实很重要的一部分效果上的提升源于对于不同视角之间的重叠区域引入了一些 stereo cues,这一点在引入时序信息时尤为重要,因为时序上相邻帧更容易形成类似于双目情形的重叠区域较大的多个视角。
而在利用这一 stereo cues 时,其实只需要简单的拼接或者 attention 操作就可以实现类似效果,如图 10 所示,BEVDet4D [21] 和 BEVFormer 对于时序特征的聚合其实就已经在利用基于匹配的 2D->3D 估计了。大家经常只关注因为引入时序而带来的速度估计上的提升,mAVE 的下降,而忽视了 mATE 和 mAP 由于定位做的更准而带来的巨大提升。
另一方面,这些方法并没有像 DfM 一样在构造 voxel feature 之前显式地利用这种 stereo cues 促进深度的估计,而是直接在 voxel 空间来进行类似操作,其实也可以实现类似效果。在我们开发 waymo 基准方法(MV-FCOS3D++)的尝试过程中,也遇到了在拓展到多视角情形下如何设计的问题。
由于不同帧不同视角(如当前帧的正前方视角和之前帧的左前方视角)之间的 stereo cues 难以在基于单目的这种方式中利用,一个更合理的方式还是利用一个中间的、统一的、显式的 voxel representation 来作为桥梁联系这些特征,这个统一的特征可以再进一步通过 LiDAR 和物体 3D 框的标注在 voxel space / frustum space 进行空间位置上的监督,本质上也可以达到和显式估计深度类似的效果。但目前这方面还没有进行过多尝试,如何高效地引入 dense depth 监督也还是一个开放问题,留待大家接着去探索。
7 讨论
虽然我们已经更加深刻地理解了在纯视觉 3D 感知中各种不同 cues 的定位和作用,也设计出了一套相对有效的 depth from motion 的框架实现了不错的效果提升,同时最近一段时间 BEV 的快速发展也极大地缩小了纯视觉和 LiDAR-based 方法的差距,但这是否意味着我们已经找到了这方面的最终解了呢?其实还有诸多问题有待进一步的探究,这里简单列举一些相关问题:
- 将这类方法部署到实际使用仍有一系列问题,如轻量化、长尾等问题
- 并没有针对性解决 depth from motion 中那些内在的困境,例如移动物体和少纹理的区域
- 仍然不确定这个性能是否足以使得做出安全的规划和决策
- 新的纯视觉方案的发展给多模态感知带来的新思路和新机遇
- 需要解决类似于基于 LiDAR 的方法中的一些挑战,如远距离和小物体的检测问题
- 虽然 BEV 获得了长足发展,是否 perspective view 就一无是处?我们在 waymo 上一些初步实验显示 perspective view 因为具有更直接的语义监督,在其之上预训练 2D backbone 会大大提升基于 BEV 方法的性能,同时也可以通过深度估计的预训练解决在 BEV 方法中引入深度估计分支带来的额外计算负担。另外 perspective view 的方法近期也并没有使用更多的一些新的 tricks,因此实际的差距或者比较可能并不像目前各大数据集基准上显示那般。这一方面依然有一些有趣的探索空间。
代码方面,一个基于 MMDetection3D 的初步版本已经开源到 https://github.com/Tai-Wang/Depth-from-Motion,目前已经支持了 DfM 在 KITTI 上和 MV-FCOS3D++ 在 Waymo 上的 benchmark,欢迎大家试用。之后这版开源 code 还会继续进行优化重构和扩展,MV-FCOS3D++ 也会在近期支持到重构后的 MMDetection3D 中,请大家持续关注。
https://github.com/open-mmlab/mmdetection3dgithub.com/open-mmlab/mmdetection3d
References:
[1] Ma, X., Zhang, Y., Xu, D., Zhou, D., Yi, S., Li, H., Ouyang, W.: Delving into localization errors for monocular 3d object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)
[2] Simonelli, A., Bulo, S.R., Porzi, L., Kontschieder, P., Ricci, E.: Are we missing confidence in pseudo-lidar methods for monocular 3d object detection? In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 3225–3233 (2021)
[3] Wang, T., Xinge, Z., Pang, J., Lin, D.: Probabilistic and geometric depth: Detecting objects in perspective. In: Conference on Robot Learning. pp. 1475–1485. PMLR (2022)
[4] Zhang, Y., Lu, J., Zhou, J.: Objects are different: Flexible monocular 3d object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)
[5] Shi, X., Ye, Q., Chen, X., Chen, C., Chen, Z., Kim, T.K.: Geometry-based distance decomposition for monocular 3d object detection. In: IEEE International Conference on Computer Vision (2021)
[6] Reading, C., Harakeh, A., Chae, J., Waslander, S.L.: Categorical depth distribution network for monocular 3d object detection. CVPR (2021)
[7] Wang, Y., Guizilini, V. C., Zhang, T., Wang, Y., Zhao, H., Solomon, J., Detr3d: 3d object detection from multi-view images via 3d-to-2d queries, in Conference on Robot Learning. PMLR, 2022, pp. 180–19
[8] Huang, J., Huang, G., Zhu, Z., Du, D., Bevdet: High-performance multi-camera 3d object detection in bird-eye-view, arXiv preprint arXiv:2112.11790, 2021
[9] Li, Z., Wang, W., Li, H., Xie, E., Sima, C., Lu, T., Qiao, Y., Dai, J., Bevformer: Learning bird’s-eye-view representation from multi-camera images via spatiotemporal transformers, arXiv preprint arXiv:2203.17270, 2022
[10] Wang, Y., Chao, W.L., Garg, D., Hariharan, B., Campbell, M., Weinberger, K.Q.: Pseudo-lidar from visual depth estimation: Bridging the gap in 3d object detection for autonomous driving. In: IEEE Conference on Computer Vision and Pattern Recognition (2019)
[11] Roddick, T., Kendall, A., Cipolla, R.: Orthographic feature transform for monocular 3d object detection. CoRR abs/1811.08188 (2018)
[12] Zhu, X., Xiong, Y., Dai, J., Yuan, L., Wei, Y.: Deep feature flow for video recognition. In: IEEE Conference on Computer Vision and Pattern Recognition (2017)
[13] Zhu, X., Wang, Y., Dai, J., Yuan, L., Wei, Y.: Flow-guided feature aggregation for video object detection. In: Proceedings of the IEEE international conference on computer vision. pp. 408–417 (2017)
[14] Chen, Y., Liu, S., Shen, X., Jia, J.: Dsgn: Deep stereo geometry network for 3d object detection. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. pp. 12536–12545 (2020)
[15] Guo, X., Shi, S., Wang, X., Li, H.: Liga-stereo: Learning lidar geometry aware representations for stereo-based 3d detector. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 3153–3163 (2021)
[16] Godard, C., Mac Aodha, O., Firman, M., Brostow, G.J.: Digging into self-supervised monocular depth estimation. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 3828–3838 (2019)
[17] Guizilini, V., Ambrus, R., Pillai, S., Raventos, A., Gaidon, A.: 3d packing for self-supervised monocular depth estimation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 2485–2494 (2020) [18] Geiger, A., Lenz, P., Urtasun, R.: Are we ready for autonomous driving? the kitti vision benchmark suite. In: IEEE Conference on Computer Vision and Pattern Recognition (2012)
[19] Brazil, G., Pons-Moll, G., Liu, X., Schiele, B.: Kinematic 3d object detection in monocular video. In: Proceedings of the European Conference on Computer Vision (2020)
[20] K¨onigshof, H., Salscheider, N.O., Stiller, C.: Realtime 3d object detection for automated driving using stereo vision and semantic information. In: 2019 IEEE Intelligent Transportation Systems Conference (ITSC). pp. 1405–1410. IEEE (2019)