CMSIS_NN：卷积神经网络

Introduction

---

物联网已经深入到我们生活的方方面面，例如穿戴式医疗设备、智能家居。大部分的物联网设备会将采集到的数据上传至云端，由后台进行数据处理和分析，再将结果返回给微处理器。然而这种云端处理数据的方式不适用于一些对实时性要求高的物联网边缘设备，通过ARM Cortex-M系列处理器内核进行Machine Learning成为了技术发展的需要，CMSIS-NN就是解决方法之一。机器学习运用到嵌入式系统中有以下的优点[1]：

• 实时性决策
• 增加数据的安全性和可靠性
• 无需依赖互联网
• 减少带宽

CMSIS-NN库分为了两个部分，NNFuctions和NNSupportFunctions，图片摘自CMSIS-NN Block Diagram。

NNFuctions运用了卷积神经网络Convolutional Neural Network(CNN)，包括了：

• Convolution Function 卷积函数
• Activations Function 激活函数
• Pooling Function 池化函数
• Fully-connected Function 全连接函数

要掌握CMSIS-NN，首先得理解CNN，所以先说一说卷积神经网络。

Convolutional Neural Network

---

Convolution

首先贴上卷积的公式，一个是连续性的，一个是离散型的：
$$(f\ast g)(n)={\int }_{-\infty }^{\infty }f(\tau )g(n-\tau )d\tau$$

$$(f\ast g)(n)=\sum _{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$$

卷积是怎么卷的？

卷积的核心在于降维。我们令$x=\tau ,y=n-\tau$，那么$x+y=n$，也就是二维平面上一条可移动的直线（图1）。当我们遍历这条直线，也就是做积分或者是求和，像是把二维平面从45°斜线卷起来，就形成了一个一维的直线函数，每个点的函数值等于卷起来后重合的点的函数值之和。这样就从一个二维函数降到了一维函数。此处参考于 荆哲：卷积为什么叫「卷」积？，非常形象地解释了“卷”的含义。

​ 图1 二维平面 x + y = n

​ 图2 一维函数

对于灰色图像的卷积，我们只需要将图像看成$m\times n$的矩形，而彩色RGB图像的卷积，我们可以将其分为Red、Green、Blue三个map，也就是深度为3，是个$m\times n\times 3$的长方体。我们首先讨论$m\times n$的2-D卷积：kernel卷积核$p\times q$在x,y方向上滑动。

kernel一般选取$3\times 3$或$5\times 5$的大小，$A_{ij}$表示权重$w$，原图像的$B_{ij}$表示图像亮度值$v$：

$$g=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right]$$
卷积的过程可以表示为：
$$con{v}_{x,y}=\sum _i^{p\ast q}{w}_i{v}_i$$
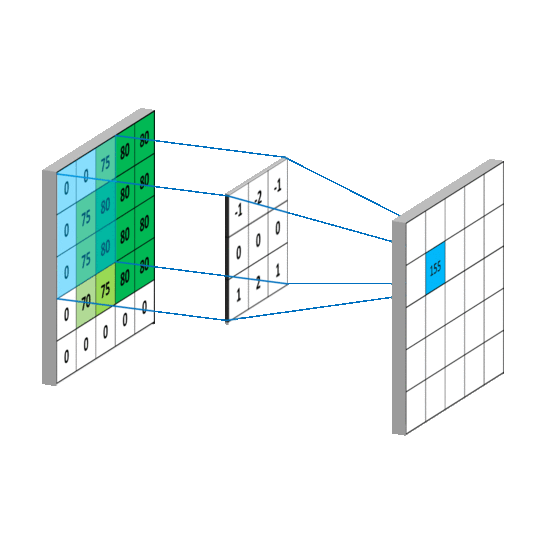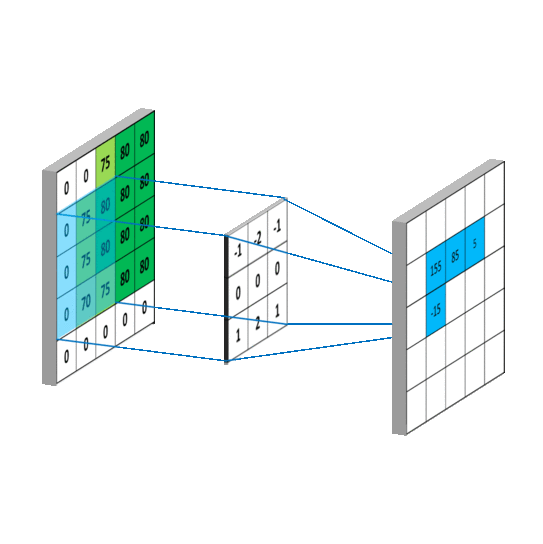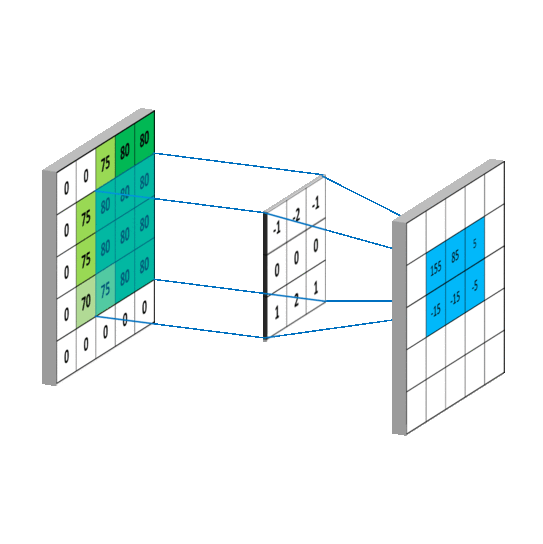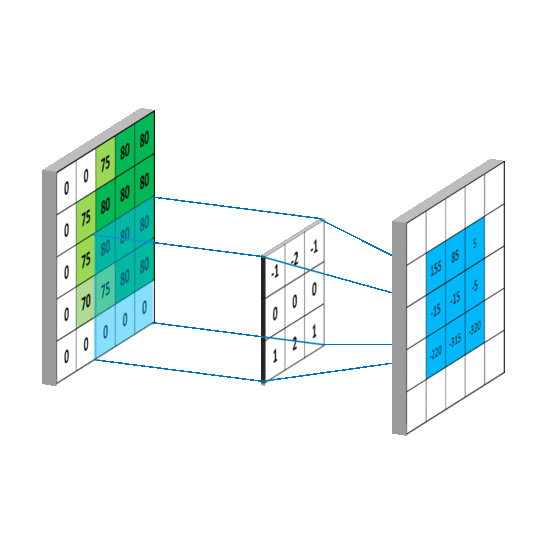
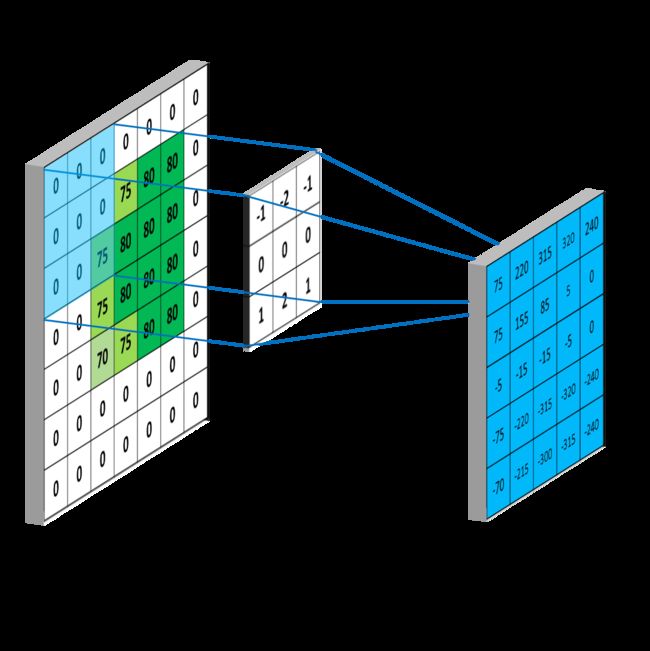
如果所示，Image Matrix和Kernel Matrix进行矩阵相乘，即0 × (-1) + 0 × (-2) + 75 × (-1) + 0 × 0 + 75 ×0 + 80 × 0 + 0 × 1 + 75 × 2 + 80 × 1 = 155 ，将该值写入Output Matrix对应的位上，这样计算出了第一个值。以下图片均来自Convolutional Neural Networks - Basics。

随后将kernel沿着$(x,y)$方向平移扫描，即可得出整个Output matrix的值。

一个$m\times n$，在不考虑边界零填充(zero padding)的情况下，输出是一个$(m-2)\times (n-2)$的矩阵。当考虑zero padding，即在$m\times n$的图像四周添加2行2列的0，输出可以得到一个和原图像大小相同的$m\times n$的矩阵。例如下图。

考虑zero padding的原因：一是对图像边缘只扫描一次的话可能会忽略边缘的信息；二是保持图像大小，不然卷积次数多了之后图像会越来越小。

kernel的个数、大小、平移步长都可以根据实际情况进行调整。

若将RGB图像分为3层进行卷积，就需要一个立体的深度为3的kernel，在x,y,z三个方向上进行扫描，此处不再论述。

Activation

激活函数的作用是给函数加入偏置：
$$Z(x,y)=h(\sum _i^{p\ast q}{w}_i{v}_i+b)$$
常用的激活函数有$Sigmoid$、$tanh$以及$ReLu$。$Sigmoid$和$tanh$函数常用于全连接层，$ReLu$函数常用语卷积层。

在CMSIS-NN中用到的激活函数是$ReLu$ Function(Rectified Linear Units Function)，作用是输出非负数，可表示为：
$$ReLu=max(0,T)$$

Pooling

池化函数的主要作用是通过特征降维对图像进行压缩，降低feature maps的分辨率，以此减少计算量，同时提高容错率。

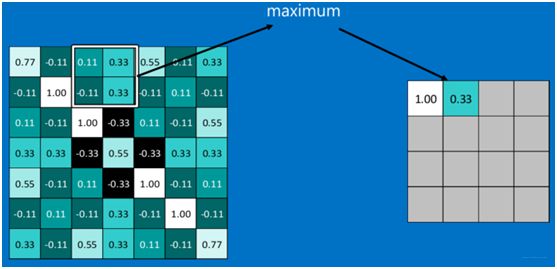
池化一般选取$2\times 2$的滑动窗口作为池化区域，通过相应的池化函数将4个像素转换为1个像素。常用的池化函数有$Max$ $ Pooling$和$Average$ $ Pooling$。

下图中采用了$Max$ $Pooling$ $Function$，在四个像素中选取了最大的数值$max(0.11,0.33,-0.11,0.33)=0.33$作为结果。例如下图。以下两张图摘自[大话卷积神经网络（CNN）][pooling and fully]。

不过并不是所有情况下，进行池化后的效果会更好，因为池化的过程中可能丢失了信息。

Fully-connected

全连接层首先将多个map经过Convolution、Activation、Pooling后的结果合并到一起，即将每个$n\times n$的矩阵都拆开转成$(n^2)\times 1$的列矩阵，再将$N$个列矩阵合并成$(n^2\times N)\times 1$的列矩阵。例如下图。

其次，根据已训练好的监督学习模型得到全连接层每一个特征值的权重，将列矩阵与权重加权求和，通过Softmax函数对数值进行分类匹配，最贴近的就是识别结果。

Conclusion

CNN算法可以分为两个部分：

• 特征提取：Convolution、Activation、Pooling
• 分类识别：Fully-connected

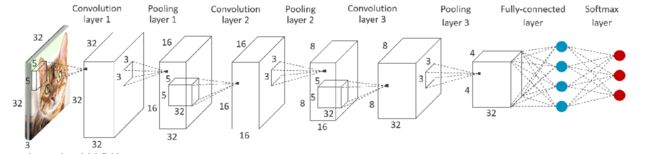
CMSIS-NN采用的是框架如下图。

使用了以下函数：

• arm_convolve_HWC_q7_RGB()
• arm_convolve_HWC_q7_fast()
• arm_relu_q7()
• arm_maxpool_q7_HWC()
• arm_avepool_q7_HWC()
• arm_fully_connected_q7_opt()
• arm_fully_connected_q7()

References

---

[1] ARM Developer, Image recognition on ARM Cortex-M with CMSIS-NN, https://developer.arm.com/solutions/machine-learning-on-arm/developer-material/how-to-guides/image-recognition-on-arm-cortex-m-with-cmsis-nn/single-page. 01 April 2019, Accessed 2020-08-19