智能优化算法之遗传算法python实现细节，GA库函数调用方法

1、基本概念

遗传算法（GA）是最早由美国Holland教授提出的一种基于自然界的“适者生存，优胜劣汰”基本法则的智能搜索算法。该法则很好地诠释了生物进化的自然选择过程。遗传算法也是借鉴该基本法则，通过基于种群的思想，将问题的解通过编码的方式转化为种群中的个体，并让这些个体不断地通过选择、交叉和变异算子模拟生物的进化过程，然后利用“优胜劣汰”法则选择种群中适应性较强的个体构成子种群，然后让子种群重复类似的进化过程，直到找到问题的最优解或者到达一定的进化（运算）时间。

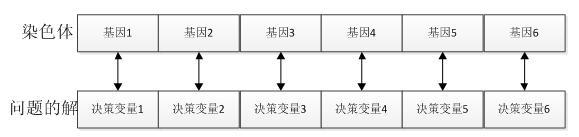
基因：在GA算法中，基因代表了具体问题解的一个决策变量，问题解和染色体中基因的对应关系如下所示：

种群：多个个体即组成一个种群。GA算法中，一个问题的多组解即构成了问题的解的种群。

2、主要步骤

GA算法的基本步骤如下：

Step 1. 种群初始化。选择一种编码方案然后在解空间内通过随机生成的方式初始化一定数量的个体构成GA的种群。

Step 2. 评估种群。利用启发式算法对种群中的个体（矩形件的排入顺序）生成排样图并依此计算个体的适应函数值（利用率），然后保存当前种群中的最优个体作为搜索到的最优解。

Step 3. 选择操作。根据种群中个体的适应度的大小，通过轮盘赌或者期望值方法，将适应度高的个体从当前种群中选择出来。

Step 4. 交叉操作。将上一步骤选择的个体，用一定的概率阀值Pc控制是否利用单点交叉、多点交叉或者其他交叉方式生成新的交叉个体。

Step 5. 变异操作。用一定的概率阀值Pm控制是否对个体的部分基因执行单点变异或多点变异。

Step 6. 终止判断。若满足终止条件，则终止算法，否则返回Step 2。

流程图如下所示：

流程图如下所示：

3、主要操作介绍

3.1 种群初始化

种群的初始化和具体的问题有关。比如一个问题有n个决策变量{x1,x2,…,xn}。每个决策变量有取值范围:下界{L1,L2,…,Ln}和上界{U1,U2,…,Un}，则种群中个体的初始化即随机地在决策变量的取值范围内生成各个决策变量的值：Xj={x1,x2,...,xn}，其中xi属于范围(Li，Ui)内。所有的个体即构成种群。当每个个体都初始化后，即种群完成初始化。

3.2 评价种群

种群的评价即计算种群中个体的适应度值。假设种群population有popsize个个体。依次计算每个个体的适应度值及评价种群。

  

遗传算法Python代码实现_大灰狼学编程的博客-CSDN博客_遗传算法python代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

# 生成X和Y的数据
X = np.arange(-5, 5, 0.1)  #生成-5，4.9之间间隔为0.1的一系列数据,100个数据
print(len(X))
Y = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(X, Y)   #对应两个数组中所有的(x,y)对

a = 10
# 目标函数
Z = 2 * a + X ** 2 - a * np.cos(2 * np.pi * X) + Y ** 2 - a * np.cos(2 * np.pi * Y)


# 绘图
fig = plt.figure()
ax = Axes3D(fig)
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
plt.show()


import numpy as np
import matplotlib.pyplot as plt

def fitness_func(X):
    # 目标函数，即适应度值，X是种群的表现型   可以通过生成参数对的形式画出的方法画出
    a = 10
    pi = np.pi
    x = X[:, 0]
    y = X[:, 1]
    return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)


def decode(x, a, b):  #x是二进制编码位数，a,b是搜索区间范围
    """解码，即基因型到表现型""" #x编码为2进值形式，转换成10进值，
    xt = 0
    for i in range(len(x)):
        xt = xt + x[i] * np.power(2, i)
    return a + xt * (b - a) / (np.power(2, len(x)) - 1)   #相当于a+Deltax

def decode_X(X: np.array):
    """对整个种群的基因解码，上面的decode是对某个染色体的某个变量进行解码"""
    #X.shape  (50,40)

    X2 = np.zeros((X.shape[0], 2))        #初始化X维50*2的全0二维数组

    for i in range(X.shape[0]):
        xi = decode(X[i, :20], -5, 5)   #X[i, :20]表示取二维数组X中第i个元素，前20个数
        yi = decode(X[i, 20:], -5, 5)   #X[i, 20：]表示取二维数组X中第i个元素，第20个之后的数
        X2[i, :] = np.array([xi, yi])    # 表示X2每个元素对取值（xi,yi)

    return X2                     #最后得到X2的全部解码

def select(X, fitness):
    """根据轮盘赌法选择优秀个体"""
    fitness = 1 / fitness  # fitness越小表示越优秀（因为是求最小值），被选中的概率越大，做 1/fitness 处理
    fitness = fitness / fitness.sum()  # 归一化
    idx = np.array(list(range(X.shape[0])))   #idx=[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49]

    X2_idx = np.random.choice(idx, size=X.shape[0], p=fitness)  # 根据概率选择 # 参数意思分别 是从idx中以概率P，随机选择size个,可能变成[ 7  1 25  7  7 43 43  1 25  7  1  7 16  1 43  1 24 43 16 25 43  1 43 24  16 43 43 43  7 25 16 43  7  7  1 49  7 43 43  7 25  7  1 25  1 16 43 43 43 16]

    X2 = X[X2_idx, :]    #X2变为挑选的编码，一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + ……… + f(Xn) ) 得到值优秀的个体选中的概率大

    return X2

def crossover(X, c):
    """按顺序选择2个个体以概率c进行交叉操作"""
    for i in range(0, X.shape[0], 2):
        xa = X[i, :]
        xb = X[i + 1, :]
        for j in range(X.shape[1]):
            # 产生0-1区间的均匀分布随机数，判断是否需要进行交叉替换
            if np.random.rand() <= c:
                xa[j], xb[j] = xb[j], xa[j]
        X[i, :] = xa
        X[i + 1, :] = xb
    return X

def mutation(X, m):
    """变异操作"""
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            if np.random.rand() <= m:
                X[i, j] = (X[i, j] + 1) % 2
    return X



def ga():
    """遗传算法主函数"""
    c = 0.3  # 交叉概率
    m = 0.05  # 变异概率
    best_fitness = []  # 记录每次迭代的效果
    best_xy = []
    iter_num = 100  # 最大迭代次数
    X0 = np.random.randint(0, 2, (50, 40))  # 随机初始化种群，为50*40的0-1矩阵，40位编码，x20位，y20位

    for i in range(iter_num):
        X1 = decode_X(X0)  # 染色体解码 得到50个（x,y)值对
        fitness = fitness_func(X1)  # 计算个体适应度 计算目标函数，得到50个目标函数值

        X2 = select(X0, fitness)  # 选择操作
        X3 = crossover(X2, c)  # 交叉操作
        X4 = mutation(X3, m)  # 变异操作
        # 计算一轮迭代的效果
        X5 = decode_X(X4)
        fitness = fitness_func(X5)
        best_fitness.append(fitness.min())
        x, y = X5[fitness.argmin()]
        best_xy.append((x, y))
        X0 = X4
    # 多次迭代后的最终效果
    print("最优值是：%.5f" % best_fitness[-1])

    print("最优解是：x=%.5f, y=%.5f" % best_xy[-1])
    # 最优值是：0.00000
    # 最优解是：x=0.00000, y=-0.00000
    # 打印效果
    plt.plot(best_fitness, color='r')
    plt.show()

ga()

最优值是：0.00000
最优解是：x=-0.00000, y=0.00000

 调用遗传算法库函数

def demo1_func(p):
    '''
This function has plenty of local minimum, with strong shocks
global minimum at (0,0) with value 0
'''

    x1, x2 = p
    print(x1,x2)
    x = x1**2+x2**2
    return x

#等式约束

def cons1(x):
    return [x[0]+x[1]-10]
cons=cons1

#遗传算法
from sko.GA import GA
import numpy as np
#2个变量，每代取50个，800次迭代，上下界及精度,精度是参数的精度,不同参数可以有不同精度，根据精度就可以对参数进行编码，约束条件是惩罚函数
#ga = GA(func=demo1_func, n_dim=2, size_pop=50, max_iter=800, lb=[-1, -1], ub=[8, 10], precision=1e-7,constraint_eq=[cons])
ga = GA(func=demo1_func, n_dim=2, size_pop=50, max_iter=800, lb=[-1, -1], ub=[80, 100], precision=[1,0.1],constraint_eq=[cons])
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)

best_x: [8.         1.96187683]  满足约束条件x+y=10
 best_y: [67.84896071]