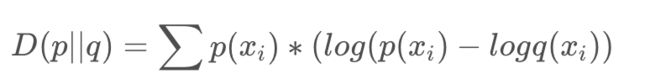对抗学习总结:FGSM->FGM->PGD->FreeAT, YOPO ->FreeLb->SMART->LookAhead->VAT
对抗训练基本思想——Min-Max公式
中括号里的含义为我们要找到一组在样本空间内、使Loss最大的的对抗样本(该对抗样本由原样本x和经过某种手段得到的扰动项r_adv共同组合得到)。这样一组样本组成的对抗样本集,它们所体现出的数据分布,就是该中括号中所体现的。
外层min()函数指的则是,我们面对这种数据分布的样本集,要通过对模型参数的更新,使模型在该对抗样本集上的期望loss最小
对抗训练的核心步骤是:
用被对抗性样本污染过的训练样本来训练模型,直到模型能学习到如此类型的抵抗。从而保证模型的安全性,在自动驾驶和图像识别领域,保证模型的安全性尤为重要。
如何找到最佳扰动r_adv呢?
很简单——梯度上升。所以说,对抗训练本质上来说,在一个step中,实际上进行了两次梯度更新,只不过是被更新的对象是不同的——首先先做梯度上升,找到最佳扰动r,使得loss最大;
其次梯度下降,找到最佳模型参数(所有层的模型参数,这一步和正常模型更新、梯度下降无异),使loss最小。 具体情况如图所示:
注:所谓“attack”,即:
它是谁:attack就是将已算出的扰动加到embedding上的操作;
它从哪来(定位在哪):attack操作是在梯度上升使loss最大、求best扰动r的过程中进行的,它的目的就是看看怎么attack才能得到最佳扰动;
它要干啥(作用):对word-embedding层attack后,计算“被attack后的loss”,即对抗loss(adv_loss),然后据此做梯度上升,对attack的扰动r进行梯度更新。
对抗学习已经在图像领域取得了不错的效果,可否将这种方式对抗训练迁移到NLP上呢?因为NLP中的输入raw_text是离散的,无法直接在raw_text上加上扰动,Goodfellow在17年提出了可以在连续的embedding上做扰动,但这样做有一个问题,训练模式时可以这样加入扰动(已知label,喂给模型是扰动后的训练样本),在模型预测时,如何加入扰动呢?(label未知,喂给模型的是正常训练样本),通常在图像领域,经过对抗训练后的模型在正常样本上表现很差,而在NLP中,由大量实验表明,对抗学习后的模型泛化能力变强了。因此在NLP任务中,对抗训练的目的不再是为了防御基于梯度的恶意攻击,反而更多的是作为一种regularization,提高模型的泛化能力。因此论文中也提到:We turn our focus away from the security benefits of adversarial training, and instead study its effects on generalization.
常见的几种对抗训练算法
FGSM (Fast Gradient Sign Method): ICLR2015
Fast Gradient Method(FGM)ICLR2017
FSGM是每个方向上都走相同的一步,Goodfellow后续提出的FGM则是根据具体的梯度进行scale,得到更好的对抗样本:
1 一切照常,计算前向loss,然后反向传播计算grad(注意这里不要更新梯度,即没有optimizer.step())
2 拿到embedding层的梯度,计算其norm,然后根据公式计算出r_adv,再将r_adv累加到原始embedding的样本上,即 x+r
3 得到对抗样本; 根据新对抗样本 x+r, 计算新loss,在backward()得到对抗样本的梯度。由于是在step(1)之后又做了一次反向传播,所以该对抗样本的梯度是累加在原始样本的梯度上的;
4 将被修改的embedding恢复到原始状态(没加上r_adv 的时候);
5 使用step(3)的梯度(原始梯度+对抗梯度),对模型参数进行更新(optimizer.step()/scheduler.step()).
class FGM():
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
由代码可知,相当于做一次对抗训练更新一次网络参数。并且每次都是在原始的embedding空间上加扰动,而非在上一次加扰动的基础上再加扰动。
Projected Gradient Descent(PGD)ICLR2018
FGM直接通过epsilon参数一下子算出了对抗扰动,这样得到的可能不是最优的。因此PGD进行了改进,多迭代几次,慢慢找到最优的扰动。
FGM简单粗暴的“一步到位”,可能走不到约束内的最优点。PGD则是“小步走,多走几步”,如果走出了扰动半径为epsilon的空间,就映射回“球面”上,以保证扰动不要过大
由上面公式(1)(2)可以看出,在一步更新网络内(公式2),在S 范围内进行了多步小的对抗训练(公式1),在这多步小的对抗训练中,对wordEmbedding空间扰动是累加的。每次都是在上一次加扰动的基础上再加扰动,然后取最后一次的梯度来更新网络参数
总览:
相比较于FGM的一步对抗到位,PGD采用小步多走的策略进行对抗。具体来说,就是一次次地进行前后向传播,一次次地根据grad计算扰动r,一次次地将新的扰动r累加到embedding层的grad上,若超出一个范围,则再映射回给定范围内。最终,将最后一步计算得到的grad累加到原始梯度上。即以累加过t步扰动的梯度对应的grad对原梯度进行更新
注意:
PGD虽不复杂,但因其两次保存/恢复操作容易搞晕——应注意的是,在K步for循环的最后一步,恢复的是梯度,因为我们要在原始梯度上进行梯度更新,更新的幅度即”累加了K次扰动的embedding权重所对应的梯度“;而在attack循环完毕、要梯度下降更新权重前,恢复的则是embedding层的权重,因为我们肯定是要在模型原始权重上做梯度下降的。
前置:设置PGD的扰动积累步数为K步
计算在正常embedding下的loss和grad(即先后进行forward、backward),在此时,将模型所有grad进行备份;
K步的for循环: # 反向传播(计算grad)是为了计算当前embedding权重下的扰动r。同时为了不干扰后序扰动r的计算,还要将每次算出的grad清零
a. 对抗攻击:如果是首步,先保存一下未经attack的grad。然后按照PGD公式以及当前embedding层的grad计算扰动,然后将扰动累加到embedding权重上;
b. if-else分支:
i. 非第K-1步时:模型当前梯度清零;
ii. 到了第K-1步时:恢复到step-1时备份的梯度(因为梯度在数次backward中已被修改);
c. 使用目前的模型参数(包括被attack后的embedding权重)以及batch_input,做前后向传播,得到loss、更新grad
恢复embedding层2.a时保存的embedding的权重(注意恢复的是权重,而非梯度)
optimizer.step(),梯度下降更新模型参数。这里使用的就是累加了K次扰动后计算所得的grad
class PGD():
def __init__(self, model, emb_name, epsilon=1., alpha=0.3):
# emb_name这个参数要换成你模型中embedding的参数名
self.model = model
self.emb_name = emb_name
self.epsilon = epsilon
self.alpha = alpha
self.emb_backup = {}
self.grad_backup = {}
def attack(self, is_first_attack=False):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0:
r_at = self.alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, self.epsilon)
def restore(self):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return self.emb_backup[param_name] + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad and param.grad is not None:
self.grad_backup[name] = param.grad.clone()
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad and param.grad is not None:
param.grad = self.grad_backup[name]
pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
FreeAT (Free Adversarial Training): NIPS2019
从FGSM到PGD,主要是优化对抗扰动的计算,虽然取得了更好的效果,但计算量也一步步增加。对于每个样本,FGSM和FGM都只用计算两次,一次是计算x的前后向,一次是计算x+r的前后向。而PGD则计算了K+1次,消耗了更多的计算资源。因此FreeAT被提了出来,在PGD的基础上进行训练速度的优化。
FreeAT的思想是在对每个样本x连续重复m次训练,计算r时复用上一步的梯度,为了保证速度,整体epoch会除以m。r的更新公式为:
伪代码:
初始化r=0 对于epoch=1…N/m:
对于每个x:
------对于每步m:
----------1.利用上一步的r,计算x+r的前后向,得到梯度
----------2.根据梯度更新参数
----------3.根据梯度更新r
缺点:
FreeLB指出,FreeAT的问题在于每次的r对于当前的参数都是次优的(无法最大化loss),因为当前r是由r(t-1)和theta(t-1)计算出来的,是对于theta(t-1)的最优。
注:
1.论文中提供伪代码,但源码中好像对1步输入做了归一化论文中并没有提到
2.个人认为可以把FreeAT当成执行m次的FGSM,最开始r=0,第一次更新的是x的梯度,之后开始迭代更新r,则根据x+r的梯度更新参数。但代码中有个问题是r只在最开始初始化,如果迭代到新的样本x2,也是根据上个样本的r进行更新的,这里我有些疑问,希望懂的大佬赐教~
代码:https://github.com/mahyarnajibi
YOPO (You Only Propagate Once): NIPS2019
代码:https://github.com/a1600012888/YOPO-You-Only-Propagate-Once
YOPO的目标也是提升PGD的效率,这篇文章需要的理论知识比较雄厚,这里只简要介绍一下。
极大值原理PMP(Pontryagin’s maximum principle)是optimizer的一种,它将神经网络看作动力学系统。这个方法的优点是在优化网络参数时,层之间是解藕的。通过这个思想,我们可以想到,既然扰动是加在embedding层的,为什么每次还要计算完整的前后向传播呢?
基于这个想法,作者想复用后几层的梯度,假设p为定值:
我们可以先写出YOPO的梯度下降版本:
对于每个样本x 初始化r(1,0) 对于j=1,2,…,m:
1.根据r(j,0),计算p 对于s=0,1,…,n-1:
2.计算r(j,s+1)
3.另r(j+1,0)=r(j,n)
作者又提出了PMP版本的YOPO,并证明SGD的YOPO是PMP版的一种特殊形式。这样每次迭代r就只用到embedding的梯度就可以了。
虽然YOPO-m-n只完成了m次完整的正反向传播,但是却实现了mn次梯度下降。而PGD-r算法完成r次完整的正反向传播却只能实现r次梯度下降。这样看来,YOPO-m-n算法的效率明显更高,而实验也表明,只要使得mn略大于r,YOPO-m-n的效果就能够与PGD-r相媲美。
然而故事的反转来的太快,FreeLB指出YOPO使用的假设对于ReLU-based网络不成立:
Interestingly, the analysis backing the extra update steps assumes a
twice continuously differentiable loss, which does not hold for
ReLU-based neural networks they experimented with, and thus the
reasons for the success of such an algorithm remains obscure.
FreeLb
代码见
FreeLB认为,FreeAT和YOPO对于获得最优r (inner max)的计算都存在问题,因此提出了一种类似PGD的方法。只不过PGD只使用了最后一步x+r输出的梯度,而FreeLB取了每次迭代r输出梯度的平均值,相当于把输入看作一个K倍大的虚拟batch,由[X+r1, X+r2, …, X+rk]拼接而成。具体的公式为:
FreeLB和PGD主要有两点区别:
1.PGD是迭代K次r后取最后一次扰动的梯度更新参数,FreeLB是取K次迭代中的平均梯度
2.PGD的扰动范围都在epsilon内,因为伪代码第3步将梯度归0了,每次投影都会回到以第1步x为圆心,半径是epsilon的圆内,而FreeLB每次的x都会迭代,所以r的范围更加灵活,更可能接近局部最优:
论文中还指出了很重要的一点,就是对抗训练和dropout不能同时使用,加上dropout相当于改变了网络结构,会影响r的计算。如果要用的话需要在K步中都使用同一个mask。
显然,相对于PGD算法,FreeLB算法保留了每步对抗训练的梯度(并且获取这些每步的梯度是没有花销的,相对PGD而言),并且均参与了网络参数的更新。而每一步对抗训练的梯度是由当前步对抗训练样本计算而来,对从模型更新的角度来说,相当于将训练样本扩大了k倍。
同时论文中又说,相对于PGD做k步对抗训练,才做一次网络参数更新。在minmax角度来说,相当于进行了多次内部maximum,然后做一次minimize。而FreeLB对每一步的max都做了minmize。论文实验部分证明了这种做法,比起PGD鲁棒性和泛化能力更强。
PGD和FreeLB的比较:
PGD是在累积扰动:
PGD每一轮都用上一轮的loss,重新计算扰动r,因为每轮计算完毕后,PGD都会model.zero_grad(),这导致每一轮算出的新扰动r_t和之前的扰动没有累加关系。这一步步的迭代,其实和经典模型训练一样,经过K次梯度上升,找到最佳δ
FreeLB每轮计算则不做model.zero_grad(),相当于每轮的 loss.backward()都在param.grad上做累加,不论是delta.grad还是其余模型的model.params.grad都是如此,所以相当于:
根据原始的正常loss -> grad_0 根据扰动r_1计算出adv_loss_1 -> grad_1 …
根据扰动r_k-1计算出adv_loss_k-1 -> grad_k-1
但以上grad永远都是在累加的,所以model.params.grad = sum(grad_0, grad_1,…,
grad_k-1),所以相当于K轮用了K个不同的、逐渐递进(这个递进指的是越来越“好”、即使adv_loss越来越大的)对抗样本(对抗样本=delta + embeds_init),用它们得到的每一次梯度一起对模型参数进行更新 所以,
可以说PGD更精确、更谨慎、更符合梯度上升的一贯作风;FreeLB更粗放、更快,论文原文还说FreeLB此举可以更容易找到最佳扰动r——具体原因是什么,我没参透…
SMART (SMoothness-inducing Adversarial Regularization)
SMART论文中提出了两个方法:
1.对抗正则 SMoothness-inducing Adversarial Regularization,提升模型鲁棒性
2.优化算法 Bregman proximal point optimization,避免灾难性遗忘
本文只介绍其中的对抗正则方法。
第一种参考了半监督对抗训练,对抗的目标是最大化扰动前后的输出,在分类任务时loss采用对称的KL散度,回归任务时使用平方损失损失:
第二种方法来自DeepMind的NIPS2019[8],核心思想是让模型学习到的流行更光滑,即让loss在训练数据呈线性变化,增强对扰动的抵抗能力。作者认为,如果loss流行足够平滑,那l(x+r)可以用一阶泰勒展开进行近似,因此用来对抗的扰动需要最大化l(x+r)和一阶泰勒展开的距离:
SMART的算法和PGD相似,也是迭代K步找到最优r,然后更新梯度。
VAT 虚拟对抗训练
论文:Adversarial Training for Large Neural Language Models
论文下载地址:https://arxiv.org/pdf/2004.08994
论文开源地址:https://github.com/namisan/mt-dnn
研究目的:解决当前的预训练模型(文中用BERT和ROBERT)泛化性和鲁棒性不足的,并且当前对抗训练虽然可以增强鲁棒性,但会损害泛化性的问题。作者还指出ALUM可以在预训练和下游任务都可以使用。
此模型是一种半监督学习的模型,相比于其他对抗式学习不同之处,例如FGSM、FGM、PGD等,对于ALUM是加入了无标签数据去优化模型参数。所以了解其他的对抗学习之后,再看看论文发现原理不会很难,以下列出几点需要提前掌握的知识点。
DL散度Loss
DL散度是量化两种概率分布P和Q之间差异的方式 :
在论文中p 是实际样本输入预训练模型输出 logits,q是指对抗样本输入预训练模型后输出adv_logits,所以这里得到模型其中的一部分Loss。
p = torch.tensor([[0.7, 0.2, 0.1], [0.2,0.2, 0.6], [0.3, 0.2, 0.5]])
q = torch.tensor([[0.6, 0.3, 0.1], [0.2,0.2, 0.6], [0.3, 0.1, 0.6]])
torch.nn.functional.kl_div(q.log_softmax(dim=-1), p.softmax(dim=-1)
模型过程
论文中给出了具体的算法过程,如下:
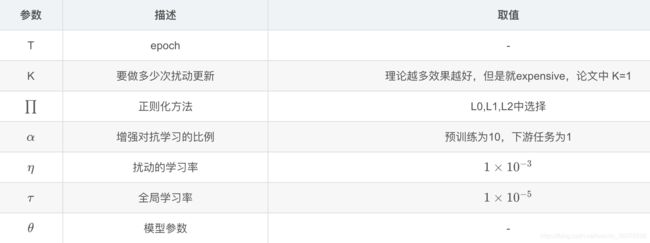
1.循环epoch
2.循环数据集,每次产生一个batch_size大小的数据
3.生成一个扰动δ , δ 服从均作为0,方差为1高斯分布
4. 循环K次,理论K越大效果越好,实际使用K=1,减少计算量
5 计算实际输入的输出和对抗样本的实际输入的DL散度Loss,并计算梯度
6 扰动正则化
7 循环K次结束
8 计算模型的Loss(带标签数据losss+虚拟对抗Loss)计算梯度更新参数,α是增强对抗学习的比例,预训练设置为10,下游任务设置为1。
最后我们需要的是最小化Loss,最大化Adv Loss,最后我们的目标是:
代码干货
代码已经开源
项目是以robert进行了实验,我们只需要关心 adv_masked_lm.py 和 adv_masked_lm_task.py 这两个文件。
adv_masked_lm.py:虚拟对抗训练代码
adv_masked_lm_task.py:训练mlm模型,其中包括超参数的设置
虚拟对抗训练代码
本人使用中是剥离出adv_masked_lm.py,方便能在torch中使用。
import torch
import torch.nn.functional as F
def kl(inputs, targets, reduction="sum"):
"""
计算kl散度
inputs:tensor,logits
targets:tensor,logits
"""
loss = F.kl_div(F.log_softmax(inputs, dim=-1),
F.softmax(targets, dim=-1),
reduction=reduction)
return loss
def adv_project(grad, norm_type='inf', eps=1e-6):
"""
L0,L1,L2正则,对于扰动计算
"""
if norm_type == 'l2':
direction = grad / (torch.norm(grad, dim=-1, keepdim=True) + eps)
elif norm_type == 'l1':
direction = grad.sign()
else:
direction = grad / (grad.abs().max(-1, keepdim=True)[0] + eps)
return direction
def virtual_adversarial_training(model, hidden_status, token_type_ids, attention_mask, logits):
"""
虚拟对抗式训练
model: nn.Module, 模型
hidden_status:tensor,input的embedded表示
token_type_ids:tensor,bert中的token_type_ids,A B 句子
attention_mask:tensor,bert中的attention_mask,对paddding mask
logits:tensor,input的输出
"""
embed = hidden_status
# 初始扰动 r
noise = embed.data.new(embed.size()).normal_(0, 1) * 1e-5
noise.requires_grad_()
# x + r
new_embed = embed.data.detach() + noise
adv_output = model(inputs_embeds=new_embed,
token_type_ids=token_type_ids,
attention_mask=attention_mask)
adv_logits = adv_output[0]
adv_loss = kl(adv_logits, logits.detach(), reduction="batchmean")
delta_grad, = torch.autograd.grad(adv_loss, noise, only_inputs=True)
norm = delta_grad.norm()
# 梯度消失,退出
if torch.isnan(norm) or torch.isinf(norm):
return None
# line 6 inner sum
noise = noise + delta_grad * 1e-3
# line 6 projection
noise = adv_project(noise, norm_type='l2', eps=1e-6)
new_embed = embed.data.detach() + noise
new_embed = new_embed.detach()
# 在进行一次训练
adv_output = model(inputs_embeds=new_embed,
token_type_ids=token_type_ids,
attention_mask=attention_mask)
adv_logits = adv_output[0]
adv_loss_f = kl(adv_logits, logits.detach())
adv_loss_b = kl(logits, adv_logits.detach())
# 在预训练时设置为10,下游任务设置为1
adv_loss = (adv_loss_f + adv_loss_b) * 1
return adv_loss
使用方法
以下是使用nezha-bert训练的调用代码:
for input_ids, token_type_ids, attention_mask, output_ids, _ in tqdm(train_loader):
step += 1
input_ids = input_ids.long().to(device)
token_type_ids = token_type_ids.long().to(device)
attention_mask = attention_mask.long().to(device)
output_ids = output_ids.long().to(device)
optimizer.zero_grad()
# 混合精度计算,训练速度接近提高了1/2
with autocast():
output = model(input_ids,
token_type_ids=token_type_ids,
attention_mask=attention_mask,
labels=output_ids)
loss = output[0]
if args.use_adv == 'vat':
logits = output[1]
hidden_status = output[2][0]
adv_loss = virtual_adversarial_training(model, hidden_status, token_type_ids, attention_mask, logits)
if adv_loss:
train_adv_loss += adv_loss
loss = adv_loss * 10 + loss
train_loss += loss
loss.backward()
optimizer.step()
转载自:
https://blog.csdn.net/Mr_tyting/article/details/103548449
https://blog.csdn.net/weixin_41712499/article/details/110878322
https://zhuanlan.zhihu.com/p/103593948
VAT : https://blog.csdn.net/weixin_40570579/article/details/115290919


![[公式]](http://img.e-com-net.com/image/info8/37eab10e434b4a7584c63738c8b67493.jpg)






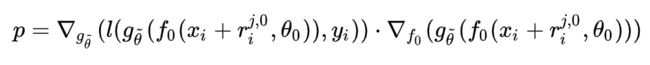






![[公式]](http://img.e-com-net.com/image/info8/b7654a8384bb4e0eb5148e236d63b274.jpg)