因子特征工程:alphalens库深度解析
原创文章第107篇,专注“个人成长与财富自由、世界运作的逻辑, AI量化投资”。
前面的文章我们把数据,因子定制,自动标注的功能都准备好了,今天继续因子分析,分析的框架当然还是alphalens。
星球有一期研报复现讲的alphalens的使用:
【每周研报复现】AI量化特征工程之alphalens:一套用于分析 alpha 因子的通用工具
qlib因子分析之alphalens源码解读
基于alphalens对qlib的alpha158做单因子分析
alphalens的使用很简单,就是整理两个数据结构,主要是对pandas dataframe的使用要熟悉。
因子数据是以date,code为双索引的dataframe格式:
而收盘价是以日期为索引,而每个资产为单独一列:
准备好的数据之后,调用utils里的get_clear_factor_and_forward_returns:
得到未来N期(默认是1天,5天和10天的收益率),因子值,以及因子分位(factor_quantile,默认从小到大分成5份)
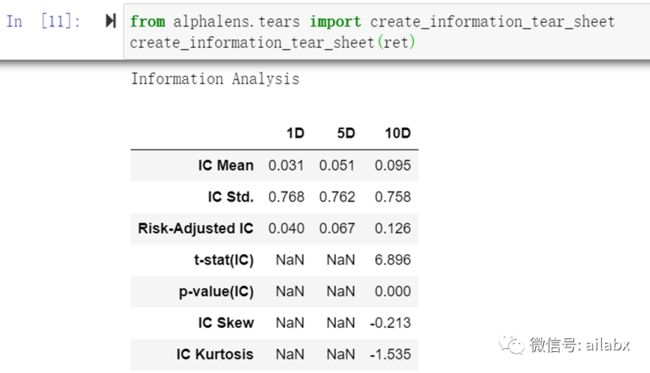
通过调用tears里的create_information_tear_sheet,得到信息分析的结果:
如上就是因子分析里的重要概念IC分析。
什么是IC呢?我们具体可以看alphalens的代码:
iC值等于同一横截面上收益率与因子的spearman相关性(就是我们熟悉的统计学中的相关系数):
stats.spearmanr( factor_data['5D'], factor_data['factor'])
生成IC表格的代码:
def plot_information_table(ic_data):
ic_summary_table = pd.DataFrame()
ic_summary_table["IC Mean"] = ic_data.mean()
ic_summary_table["IC Std."] = ic_data.std()
ic_summary_table["Risk-Adjusted IC"] = \
ic_data.mean() / ic_data.std()
t_stat, p_value = stats.ttest_1samp(ic_data, 0)
ic_summary_table["t-stat(IC)"] = t_stat
ic_summary_table["p-value(IC)"] = p_value
ic_summary_table["IC Skew"] = stats.skew(ic_data)
ic_summary_table["IC Kurtosis"] = stats.kurtosis(ic_data)
print("Information Analysis")
utils.print_table(ic_summary_table.apply(lambda x: x.round(3)).T)
可以看出来,IC值是每个截面的因子值与未来某期收益率的相关系数,然后对这个相关系数序列均值,标准差,偏度,峰度等等。风险调整后的IC就是IC均值/IC标准差。
一般而言,看RIC达到0.05以上认为相关性显著。
IC值越大越好。上面的例子中,20日动量与未来1天,5天及10天都有较显著的相关性,说明这是一个比较有效的因子。
收益分析:
先说后面三列,Top Quantile就是因子值最高的与最低的,两个构建组合。Spread就是两者之间的差。
Alpha与Beta:
这里的y是因子收益率,x是因子值,与IC不同,IC是两者之间的相关系数,而Alpha,Beta是二者之间的线性拟合。
alpha_beta = pd.DataFrame()
for period in returns.columns.values:
x = universe_ret[period].values
y = returns[period].values
x = add_constant(x)
@plotting.customize
def create_returns_tear_sheet(
factor_data, long_short=True, group_neutral=False, by_group=False
):
factor_returns = perf.factor_returns(
factor_data, long_short, group_neutral
)
mean_quant_ret, std_quantile = perf.mean_return_by_quantile(
factor_data,
by_group=False,
demeaned=long_short,
group_adjust=group_neutral,
)
mean_quant_rateret = mean_quant_ret.apply(
utils.rate_of_return, axis=0, base_period=mean_quant_ret.columns[0]
)
mean_quant_ret_bydate, std_quant_daily = perf.mean_return_by_quantile(
factor_data,
by_date=True,
by_group=False,
demeaned=long_short,
group_adjust=group_neutral,
)
mean_quant_rateret_bydate = mean_quant_ret_bydate.apply(
utils.rate_of_return,
axis=0,
base_period=mean_quant_ret_bydate.columns[0],
)
compstd_quant_daily = std_quant_daily.apply(
utils.std_conversion, axis=0, base_period=std_quant_daily.columns[0]
)
alpha_beta = perf.factor_alpha_beta(
factor_data, factor_returns, long_short, group_neutral
)
mean_ret_spread_quant, std_spread_quant = perf.compute_mean_returns_spread(
mean_quant_rateret_bydate,
factor_data["factor_quantile"].max(),
factor_data["factor_quantile"].min(),
std_err=compstd_quant_daily,
)
fr_cols = len(factor_returns.columns)
vertical_sections = 2 + fr_cols * 3
gf = GridFigure(rows=vertical_sections, cols=1)
plotting.plot_returns_table(
alpha_beta, mean_quant_rateret, mean_ret_spread_quant
)
plotting.plot_quantile_returns_bar(
mean_quant_rateret,
by_group=False,
ylim_percentiles=None,
ax=gf.next_row(),
)
plotting.plot_quantile_returns_violin(
mean_quant_rateret_bydate, ylim_percentiles=(1, 99), ax=gf.next_row()
)
trading_calendar = factor_data.index.levels[0].freq
if trading_calendar is None:
trading_calendar = pd.tseries.offsets.BDay()
warnings.warn(
"'freq' not set in factor_data index: assuming business day",
UserWarning,
)
# Compute cumulative returns from daily simple returns, if '1D'
# returns are provided.
if "1D" in factor_returns:
title = (
"Factor Weighted "
+ ("Group Neutral " if group_neutral else "")
+ ("Long/Short " if long_short else "")
+ "Portfolio Cumulative Return (1D Period)"
)
plotting.plot_cumulative_returns(
factor_returns["1D"], period="1D", title=title, ax=gf.next_row()
)
plotting.plot_cumulative_returns_by_quantile(
mean_quant_ret_bydate["1D"], period="1D", ax=gf.next_row()
)
ax_mean_quantile_returns_spread_ts = [
gf.next_row() for x in range(fr_cols)
]
plotting.plot_mean_quantile_returns_spread_time_series(
mean_ret_spread_quant,
std_err=std_spread_quant,
bandwidth=0.5,
ax=ax_mean_quantile_returns_spread_ts,
)
plt.show()
gf.close()
if by_group:
(
mean_return_quantile_group,
mean_return_quantile_group_std_err,
) = perf.mean_return_by_quantile(
factor_data,
by_date=False,
by_group=True,
demeaned=long_short,
group_adjust=group_neutral,
)
mean_quant_rateret_group = mean_return_quantile_group.apply(
utils.rate_of_return,
axis=0,
base_period=mean_return_quantile_group.columns[0],
)
num_groups = len(
mean_quant_rateret_group.index.get_level_values("group").unique()
)
vertical_sections = 1 + (((num_groups - 1) // 2) + 1)
gf = GridFigure(rows=vertical_sections, cols=2)
ax_quantile_returns_bar_by_group = [
gf.next_cell() for _ in range(num_groups)
]
plotting.plot_quantile_returns_bar(
mean_quant_rateret_group,
by_group=True,
ylim_percentiles=(5, 95),
ax=ax_quantile_returns_bar_by_group,
)
plt.show()
gf.close()
不同分位计算收益率;
按分位数做投资组合,比如quantile=1的加权平均做一个组合,quanttile=5的做另一个组合。
我们只有3支,只形成三个分位段,这样形成按分位的组合序列:
小结:
今天重点分析了alphalens的IC分析与收益分析。IC分析是其中最重要的,就是单因子与预期收益之间的相关关系。
而收益分析类似“回测”,即买入因子最高分位的收益率是多少,最低分位的收益率是多少,两者多空的利差是多少。另外收益率与因子值做线性拟合,得到alpha和beta。
最新代码与数据,请前往星球量化专栏下载。